Работа газа при изменении его объема

ТЕМА 7. ОСНОВЫ ТЕРМОДИНАМИКИ И ЕЕ СВЯЗЬ С

МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИЕЙ ИДЕАЛЬНЫХ ГАЗОВ

Внутренняя энергия. Количество теплоты. Работа газа при изменении его объема. Первое начало термодинамики.

Рассмотрим термодинамическую систему, для которой механическая энергия не изменяется, а изменяется лишь ее внутренняя энергия.

Внутренняя энергия –энергия хаотического (теплового) движения микрочастиц системы (молекул, атомов, электронов, ядер и т.д.), т.е. энергия поступательного и вращательного движения молекул и колебательного движения атомов в молекулах и энергия межмолекулярного взаимодействия.

Во внутреннюю энергию также входят внутримолекулярная химическая; внутриатомная; внутриядерная; гравитационная (взаимодействие между молекулами); лучистая (в пространстве между молекулами). Однако в нашем курсе термодинамики эти составляющие внутренней энергии рассматриваться не будут, поскольку мы ограничимся в основном рассмотрением термодинамики идеальных газов.

Существуют два пути изменения внутренней энергии:

а) совершение работы над системой;

б) сообщение системе тепла.

Внутренняя энергия идеального газа определяется выражением:

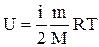, (7.1.1)

где 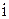- число степеней свободы. Из формулы (7.1.1) видно, что внутренняя энергия идеального газа зависит (для данной массы газа) только от его температуры и, следовательно, является параметром состояния, т.е. не зависит от пути перехода газа в данное состояние.

Изменение внутренней энергии идеального газа при этом также будет однозначно определяться только изменением температуры газа и не будет зависеть от вида процесса: 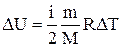(7.1.2)

или для бесконечно малого изменения температуры:

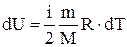(7.1.3)

Работа газа при изменении его объема.

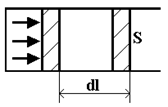Рассмотрим работу, совершаемую газом при изменении его объема (рис.7.1).

Газ, расширяясь, передвигает поршень на dl и производит над ним работу, равную:

dA = Fdl cos0 = Fdl = pSdl = pdV

=> Элементарная работа газа при изменении его объема: dA = pdV. (7.1.4)

Рис.7.1

Тогда полная работа газа по изменению объема от V₁ до V₂:

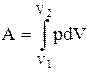(7.1.5.).

Результат интегрирования определяется характером зависимости между давлением и объемом газа, таким образом, работа газа является функцией процесса и зависит от пути перехода системы из одного состояния в другое. Найденное для работы выражение (7.1.5.) справедливо при любых изменениях объема твердых, жидких и газообразных тел.

Энергия механического движения может превращаться в энергию теплового движения и наоборот. При этих превращениях должен соблюдаться закон сохранения и превращения энергии, чем по существу и является, применительно к термодинамике, первое начало, установленное в результате обобщения многовековых опытных данных.

Пусть имеется некоторая система (газ, заключенный в цилиндр). U₁ - ее внутренняя энергия. После того, как она получила некоторое количество теплоты Q, система перешла в состояние U₂ и совершила работу А против внешних сил.

Q>0 , если тепло подводится к системе ; и наоборот .

А>0 , если система совершает ее против внешних сил.

Опыт показывает, что при переходе из U₁ в U₂ ( 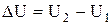) справедливо равенство:

;

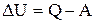или 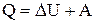; (7.1.6)

или для бесконечно малых приращений (в дифференциальной форме):

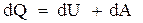, (7.1.7)

где 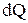- бесконечно малое количество тепла, переданное системе,

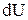- бесконечно малое изменение внутренней энергии,

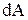- бесконечно малая (элементарная) работа.

Выражения (7.1.6) и (7.1.7) являются математической записью первого начала термодинамики.

Первое начало термодинамики:теплота, сообщаемая системе, расходуется на изменение ее внутренней энергии и на совершение системой работы против внешних сил.

Если система периодически возвращается в первоначальное состояние, то изменение ее внутренней энергии 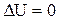. Тогда, согласно первому началу термодинамики,

,

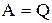т.е. вечный двигатель первого рода – периодически действующий двигатель, который совершал бы большую работу, чем сообщенная ему извне энергия, - невозможен (одна из формулировок первого начала термодинамики).