Магнитный момент контура с током
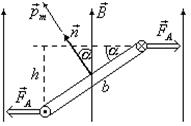 |
Магнитное поле оказывает ориентирующее действие на рамку с током, располагая ее правовинтовую нормаль по отношению к току по полю. При отклонении рамки от этого положения на неё будет действовать вращающий момент. Действительно. На каждую сторону рамки действует сила Ампера 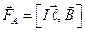 направления, которых определится по правилу левой руки, а по модулю
направления, которых определится по правилу левой руки, а по модулю 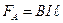 .
.
В данном случае эти силы образуют пару сил, создающих вращающий момент
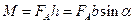 ,
,
где 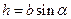 — плечо пары сил (см. рисунок). Подставив, выражение силы Ампера, получим
— плечо пары сил (см. рисунок). Подставив, выражение силы Ампера, получим 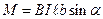 . Площадь рамки (площадь поверхности, натянутой на каркас рамки)
. Площадь рамки (площадь поверхности, натянутой на каркас рамки) 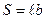 , тогда
, тогда 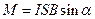 .
.
Эта формула будет сходна с формулой вращательного момента, действующего на электрический диполь, если ввести понятие магнитного момента 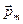 .
.
Магнитным моментом контура с током 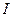 называется векторная величина
называется векторная величина 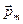 , равная
, равная
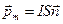 ,
,
где 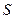 — площадь поверхности, натянутой на контур с током (ограниченной этим контуром),
— площадь поверхности, натянутой на контур с током (ограниченной этим контуром), 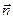 — единичный вектор нормали к этой поверхности, образующей с током правовинтовую систему. Вектора
— единичный вектор нормали к этой поверхности, образующей с током правовинтовую систему. Вектора 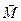 ,
, 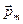 и
и  взаимно перпендикулярны и образуют правовинтовую тройку, что позволяет записать выражение для вращающего момента в векторном виде
взаимно перпендикулярны и образуют правовинтовую тройку, что позволяет записать выражение для вращающего момента в векторном виде
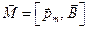 ,
,
а модуль о вектора 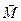 равен
равен 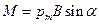 . Этот результат справедлив не только для рамки с током, но и для любого замкнутого контура с током произвольной формы.
. Этот результат справедлив не только для рамки с током, но и для любого замкнутого контура с током произвольной формы.
Определим потенциальную энергию контура с током в магнитном поле. Для того чтобы увеличить угол между моментом 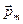 и индукцией
и индукцией  на
на 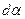 необходимо совершить работу
необходимо совершить работу
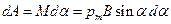 .
.
Эта работа равна увеличению потенциальной энергии контура с током в магнитном поле
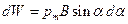 .
.
Тогда 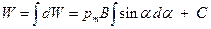 , или
, или 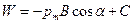 . Константу интегрирования
. Константу интегрирования 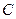 определим из условия: если
определим из условия: если 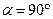 , то
, то 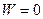 . В этом случае
. В этом случае 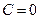 и, следовательно,
и, следовательно,
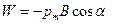 . В векторной форме
. В векторной форме
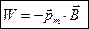 .
.
Минимум энергии соответствует углу 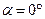 ,
, 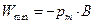 , а максимум энергии соответствует углу
, а максимум энергии соответствует углу 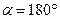 ,
, 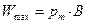 .
.
Выразив магнитный момент как 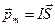 , можно записать потенциальную энергию контура с током в другом виде
, можно записать потенциальную энергию контура с током в другом виде 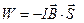 . Скалярное произведение
. Скалярное произведение 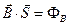 есть поток магнитной индукции через поверхность контура, тогда
есть поток магнитной индукции через поверхность контура, тогда
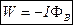
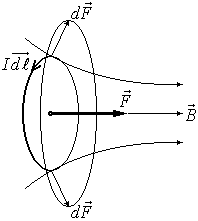 |
Внесем теперь плоский контур с током в неоднородное магнитное поле. Предположим, что поле увеличивается быстрее всего в направлении оси 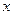 , совпадающем с направлением поля
, совпадающем с направлением поля  в месте расположения центра контура, и магнитный момент контура
в месте расположения центра контура, и магнитный момент контура 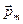 ориентирован по полю.
ориентирован по полю.
Силы 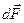 , действующие на элементы контура перпендикулярны к векторам
, действующие на элементы контура перпендикулярны к векторам  и
и 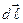 , и образуют симметричный конический веер. Их результирующая сила
, и образуют симметричный конический веер. Их результирующая сила 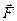 направлена в сторону возрастания вектора
направлена в сторону возрастания вектора  и втягивает контур в область более сильного поля.
и втягивает контур в область более сильного поля.
Если изменить направление тока на обратное, направление всех сил 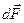 и их результирующая сила
и их результирующая сила 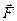 изменят, также свое направление на обратное и контур с током будет выталкиваться из магнитного поля.
изменят, также свое направление на обратное и контур с током будет выталкиваться из магнитного поля.
