Основы молекулярной физики и термодинамики
Молекулярно – кинетическая теория идеальных газов
· Закон Бойля – Мариотта (изотермический процесс):
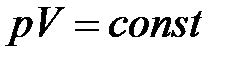 при
при 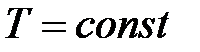 ,
, 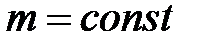 ,
,
где 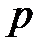 – давление, Па;
– давление, Па; 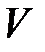 – объем, м3;
– объем, м3; 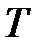 – термодинамическая температура, К;
– термодинамическая температура, К; 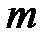 – масса газа, кг.
– масса газа, кг.
· Закон Гей-Люссака (изобарный процесс):
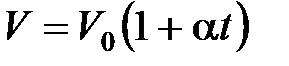 , или
, или 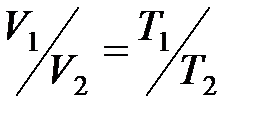 при
при 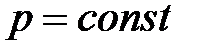 ,
, 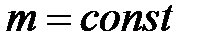 ;
;
· Закон Шарля (изохорный процесс):
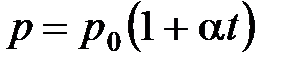 , или
, или 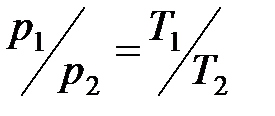 при
при 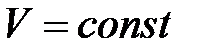 ,
, 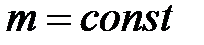 ,
,
где 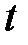 – температура по шкале Цельсия, °C;
– температура по шкале Цельсия, °C; 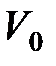 и
и 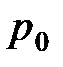 – соответственно объем и давление при
– соответственно объем и давление при 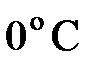 ; коэффициент
; коэффициент 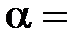 1/273 К-1; индексы 1 и 2 относятся к произвольным состояниям.
1/273 К-1; индексы 1 и 2 относятся к произвольным состояниям.
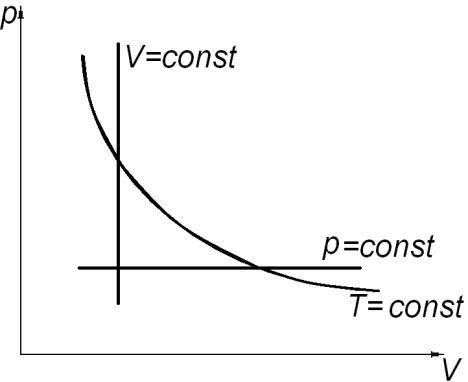
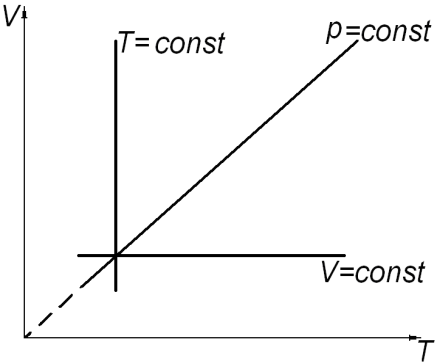
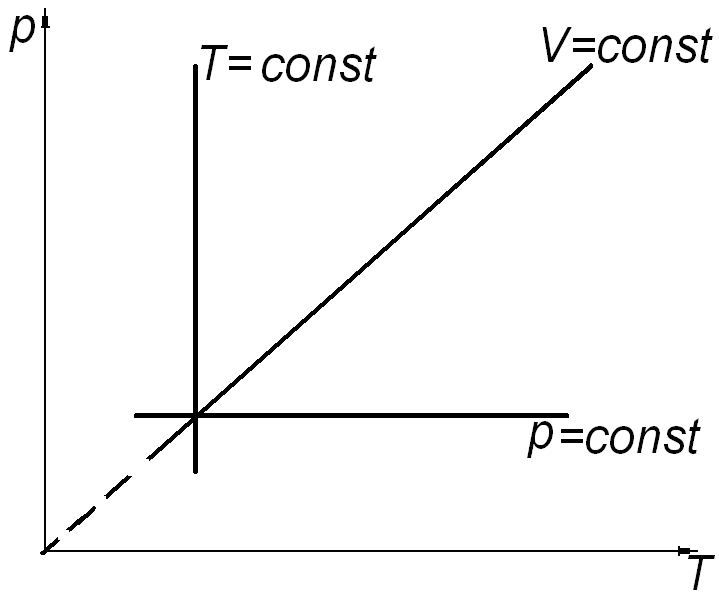
а) б) в)
Рис. 2.
Состояние системы, находящейся в тепловом равновесии, изображают точкой на плоскости в прямоугольной системе координат, на осях которой откладывают в зависимости от условий задачи параметры: p, V (рис. 2. а); V, T (рис. 2. б); p, T (рис. 2. в). Равновесный процесс, в котором участвует газ, изображают в виде графиков между соответствующими параметрами p и V; V и T; p и T. На диаграммах (рис. 2. а, б, в) представлены графики изопроцессов в различных системах координат.
· Закон Дальтона для давления смеси п идеальных газов
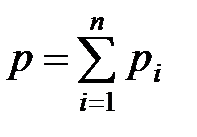 ,
,
где 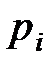 – парциальное давление
– парциальное давление 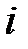 -го компонента смеси.
-го компонента смеси.
· Уравнение состояния идеального газа (уравнение Клапейрона – Менделеева)
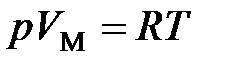 (для 1 моль газа),
(для 1 моль газа),
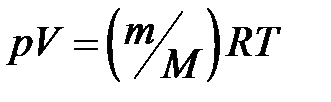 (для произвольной массы газа),
(для произвольной массы газа),
где 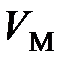 – молярный объем, м3/моль;
– молярный объем, м3/моль; 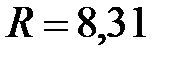 Дж/(моль×К) – молярная универсальная газовая постоянная;
Дж/(моль×К) – молярная универсальная газовая постоянная; 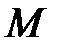 – молярная масса газа, кг/моль;
– молярная масса газа, кг/моль; 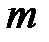 – масса газа, кг;
– масса газа, кг; 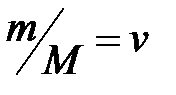 – количество вещества, моль.
– количество вещества, моль.
· Зависимость давления газа от концентрации п молекул и температуры 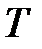
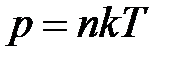 ,
,
где 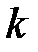 – постоянная Больцмана (
– постоянная Больцмана ( 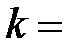 R/Na,
R/Na, 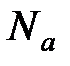 – постоянная Авогадро); n = N/V – концентрация молекул, м-3.
– постоянная Авогадро); n = N/V – концентрация молекул, м-3.
· Основное уравнение молекулярно-кинетической теории идеальных газов
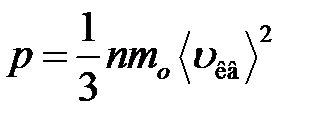 ,
,
или
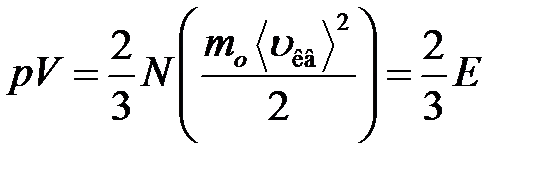 ,
,
или
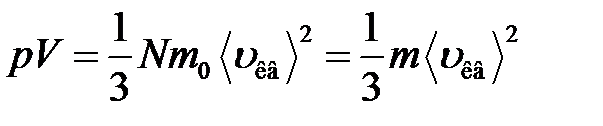 ,
,
где 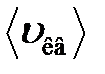 – средняя квадратичная скорость молекул;
– средняя квадратичная скорость молекул; 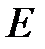 – суммарная кинетическая энергия поступательного движения всех молекул газа; п – концентрация молекул;
– суммарная кинетическая энергия поступательного движения всех молекул газа; п – концентрация молекул; 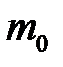 – масса одной молекулы;
– масса одной молекулы; 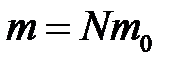 – масса газа; N – число молекул в объеме газа V.
– масса газа; N – число молекул в объеме газа V.
· Скорость молекул:
наиболее вероятная
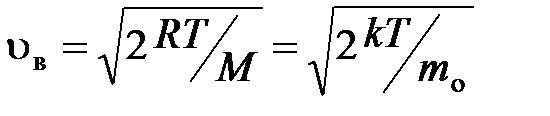 ;
;
средняя квадратичная
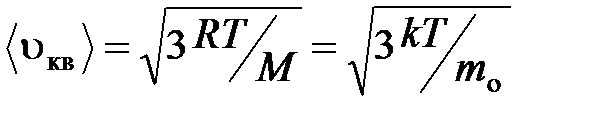 ;
;
средняя арифметическая
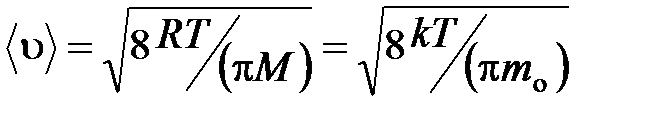 .
.
· Средняя кинетическая энергия поступательного движения молекулы идеального газа
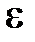 0 = 3kT/2.
0 = 3kT/2.
· Закон Максвелла для распределения молекул идеального газа по скоростям
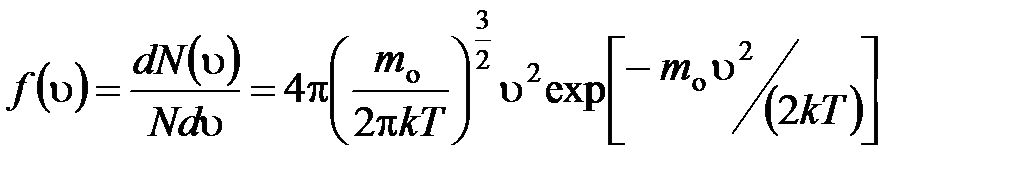 ,
,
где 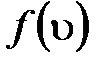 – функция распределения молекул по скоростям, которая определяет относительное число молекул
– функция распределения молекул по скоростям, которая определяет относительное число молекул 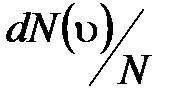 из общего числа N молекул, скорости которых лежат в интервале от
из общего числа N молекул, скорости которых лежат в интервале от 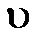 до
до 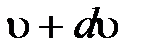 .
.
· Закон Максвелла для распределения молекул идеального газа по энергиям теплового движения
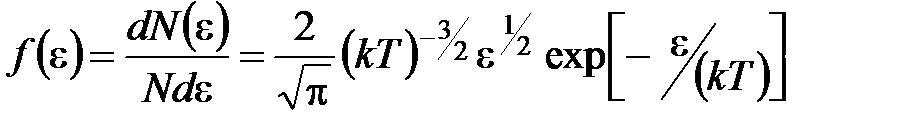 ,
,
где 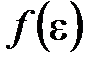 – функция распределения молекул по энергиям теплового движения, которая определяет относительное число молекул
– функция распределения молекул по энергиям теплового движения, которая определяет относительное число молекул 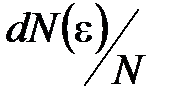 из общего числа N молекул, имеющие кинетические энергии
из общего числа N молекул, имеющие кинетические энергии 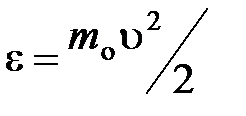 , заключенные в интервале от
, заключенные в интервале от 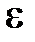 до
до 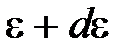 .
.
· Барометрическая формула
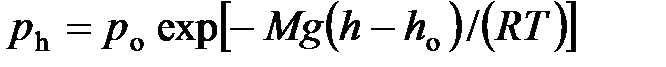 ,
,
где 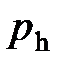 и
и 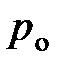 давление газа на высоте
давление газа на высоте 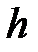 и
и 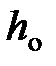 .
.
· Распределение Больцмана во внешнем потенциальном поле
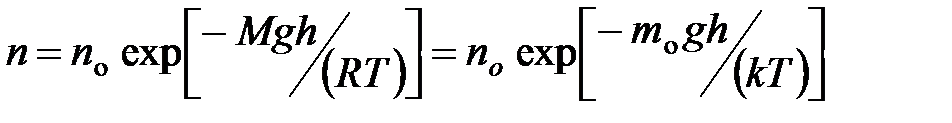 ,
,
где п и 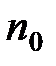 – концентрация молекул на высоте
– концентрация молекул на высоте 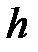 и
и 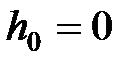 ;
; 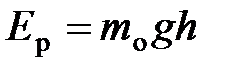 – потенциальная энергия молекулы в поле тяготения.
– потенциальная энергия молекулы в поле тяготения.
· Среднее число соударений, испытываемых молекулой газа за 1 с:
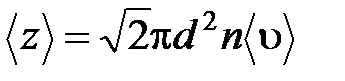 ,
,
где 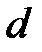 –эффективный диаметр молекулы; п – концентрация молекул;
–эффективный диаметр молекулы; п – концентрация молекул; 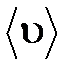 – средняя арифметическая скорость молекул.
– средняя арифметическая скорость молекул.
· Средняя длина свободного пробега молекул газа
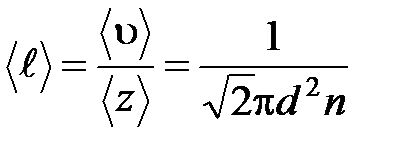 .
.
· Закон теплопроводности Фурье
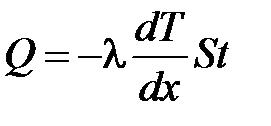 ,
,
где 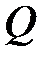 – теплота, прошедшая посредством теплопроводности через площадь
– теплота, прошедшая посредством теплопроводности через площадь 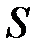 за время
за время 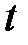 ;
; 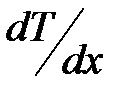 – градиент температуры;
– градиент температуры; 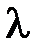 – теплопроводность:
– теплопроводность:
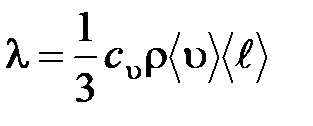 ,
,
где 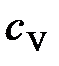 – удельная теплоемкость газа при постоянном объеме; ρ – плотность газа;
– удельная теплоемкость газа при постоянном объеме; ρ – плотность газа; 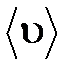 – средняя арифметическая скорость теплового движения его молекул;
– средняя арифметическая скорость теплового движения его молекул; 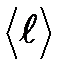 – средняя длина свободного пробега молекул.
– средняя длина свободного пробега молекул.
· Закон диффузии Фика
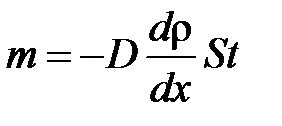 ,
,
где 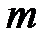 – масса вещества, переносимая посредством диффузии через площадь
– масса вещества, переносимая посредством диффузии через площадь 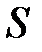 за время
за время 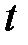 ;
; 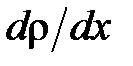 – градиент плотности,
– градиент плотности, 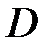 – диффузия:
– диффузия:
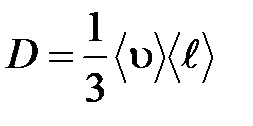 .
.
· Закон Ньютона для внутреннего трения (вязкости)
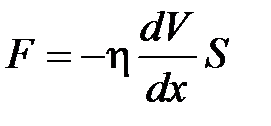 ,
,
где 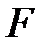 – сила внутреннего трения между движущимися слоями площадью
– сила внутреннего трения между движущимися слоями площадью 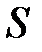 ;
; 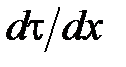 – градиент скорости;
– градиент скорости; 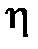 – динамическая вязкость Па×с:
– динамическая вязкость Па×с:
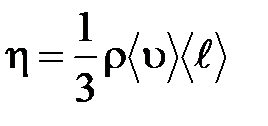 .
.
Основы термодинамики
· Средняя кинетическая энергия поступательного движения, приходящаяся на одну степень свободы молекул,
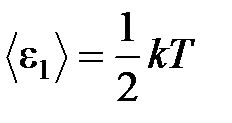 .
.
· Средняя энергия молекулы
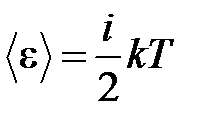 ,
,
где 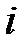 – сумма поступательных, вращательных и удвоенного числа колебательных степеней свободы
– сумма поступательных, вращательных и удвоенного числа колебательных степеней свободы 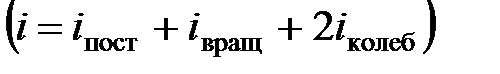 .
.
· Внутренняя энергия идеального газа
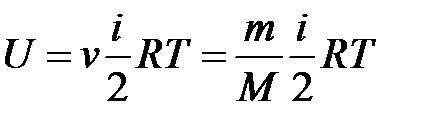 ,
,
где 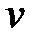 – количество вещества;
– количество вещества; 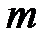 – масса газа;
– масса газа; 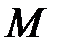 – молярная масса газа;
– молярная масса газа; 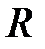 – универсальная газовая постоянная.
– универсальная газовая постоянная.
· Первое начало термодинамики
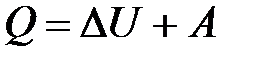 ,
,
где 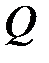 – количество теплоты, сообщенное системе или отданное ею;
– количество теплоты, сообщенное системе или отданное ею; 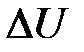 – изменение ее внутренней энергии;
– изменение ее внутренней энергии; 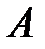 – работа системы против внешних сил.
– работа системы против внешних сил.
· Первое начало термодинамики для малого изменения состояния системы
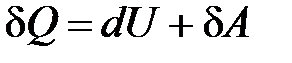 .
.
· Связь между молярной 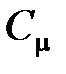 и удельной
и удельной 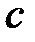 теплоемкостями газа
теплоемкостями газа
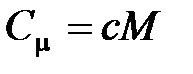 ,
,
где 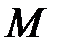 – молярная масса газа.
– молярная масса газа.
· Молярные теплоемкости газа при постоянном объеме и постоянном давлении
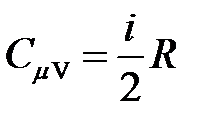 ,
, 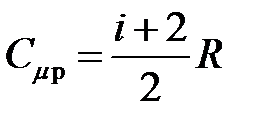 .
.
· Уравнение Майера
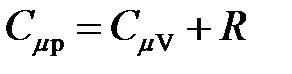 .
.
· Изменение внутренней энергии идеального газа
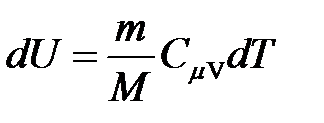 .
.
· Работа, совершаемая газом при изменении его объема:
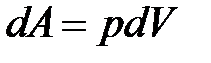 .
.
· Полная работа при изменении объема газа
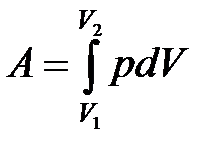 ,
,
где 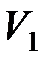 и
и 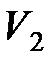 – соответственно начальный и конечный объемы газа.
– соответственно начальный и конечный объемы газа.
· Работа газа:
при изобарном процессе
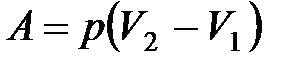 или
или 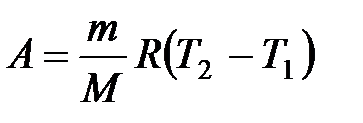 ;
;
при изотермическом процессе
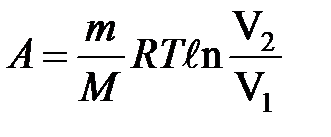 или
или 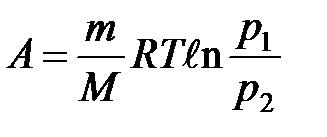 .
.
· Уравнение адиабатного процесса (уравнение Пуассона)
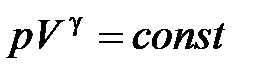 ,
, 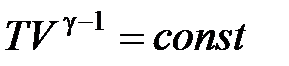 ,
, 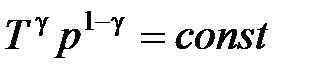 ,
,
где 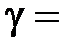 Cp/CV = (i + 2)/i – показатель адиабаты.
Cp/CV = (i + 2)/i – показатель адиабаты.
· Работа в случае адиабатного процесса
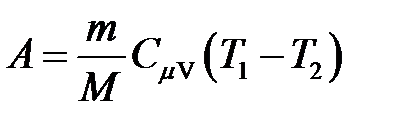 , или
, или
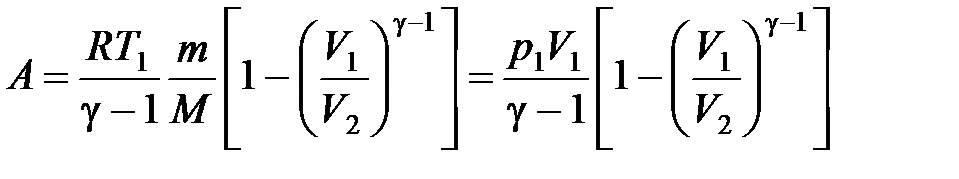 ,
,
где 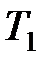 ,
, 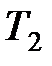 , и
, и 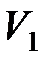 ,
, 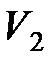 – соответственно начальные и конечные температура и объем газа.
– соответственно начальные и конечные температура и объем газа.
· Термический коэффициент полезного действия для кругового процесса (цикла)
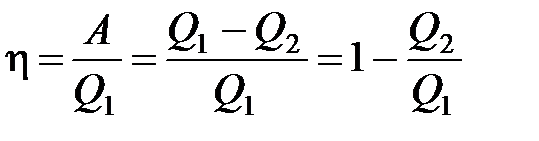 ,
,
где 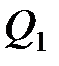 – количество теплоты, полученное системой;
– количество теплоты, полученное системой; 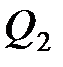 – количество теплоты, отданное системой;
– количество теплоты, отданное системой; 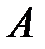 – работа, совершаемая за цикл.
– работа, совершаемая за цикл.
· Термический коэффициент полезного действия цикла Карно
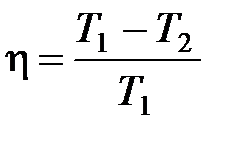 ,
,
где 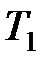 – температура нагревателя;
– температура нагревателя; 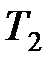 – температура холодильника.
– температура холодильника.
· Изменение энтропии при равновесном переходе из состояния 1 в состояние 2
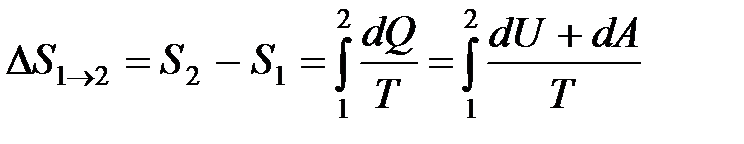 .
.
Статистическое толкование энтропии приводит к расчетной зависимости
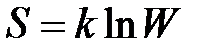 ,
,
где 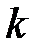 – постоянная Больцмана,
– постоянная Больцмана, 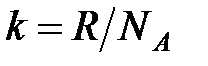 ;
; 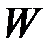 – термодинамическая вероятность.
– термодинамическая вероятность.
Для одного моля идеального газа
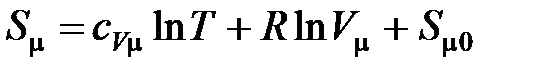 ,
,
где 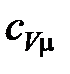 – изохорная молярная теплоемкость газа,
– изохорная молярная теплоемкость газа, 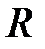 – универсальная газовая постоянная,
– универсальная газовая постоянная, 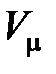 – молярный объем,
– молярный объем, 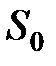 – энтропия одного моля, принятая за начало отсчета.
– энтропия одного моля, принятая за начало отсчета.
Реальные газы, жидкости
И твердые тела
· Уравнение состояния реальных газов (уравнение Ван-дер-Ваальса) для моля газа
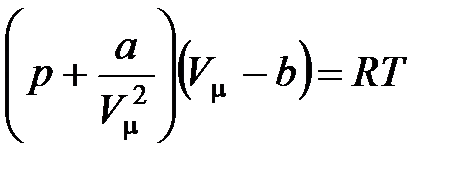 ,
,
где 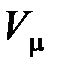 – молярный объем; а и
– молярный объем; а и 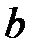 – постоянные Ван-дер-Ваальса, различные для разных газов.
– постоянные Ван-дер-Ваальса, различные для разных газов.
· Уравнение Ван-дер-Ваальса для произвольной массы газа
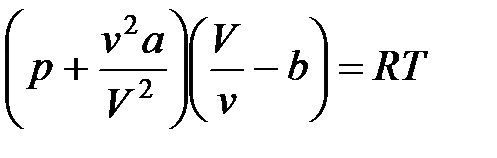 , или
, или 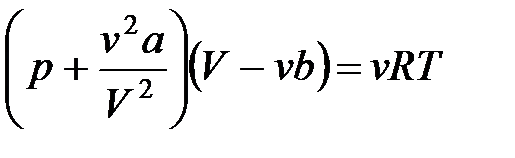 ,
,
где 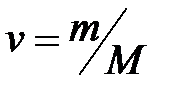 – количество вещества.
– количество вещества.
· Внутреннее давление, обусловленное силами взаимодействия молекул,
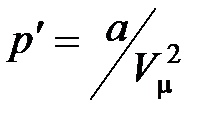 .
.
· Связь критических параметров – объема, давления и температуры – с постоянными а и 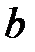 Ван-дер-Ваальса:
Ван-дер-Ваальса:
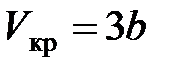 ,
, 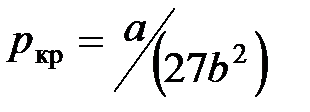 ,
, 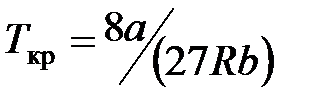 .
.
Отсюда можно получить соотношение между постоянными Ван-дер-Ваальса и параметрами критического состояния, используя понятия приведенных температуры t, давления p и объема w:
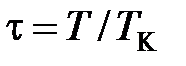 ;
; 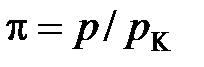 ;
; 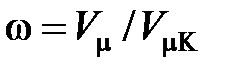 .
.
Уравнение Ван-дер-Ваальса для одного моля газа в приведенной форме имеет вид:
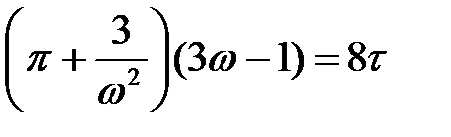 .
.
· Внутренняя энергия произвольной массы реального газа
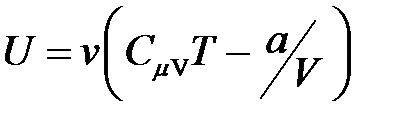 ,
,
·
· Поверхностное натяжение
σ = F/ 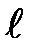 , или σ = ΔE/ΔS,
, или σ = ΔE/ΔS,
где 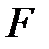 – сила поверхностного натяжения, действующая на контур
– сила поверхностного натяжения, действующая на контур 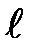 , ограничивающий поверхность жидкости;
, ограничивающий поверхность жидкости; 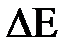 – поверхностная энергия, связанная с площадью
– поверхностная энергия, связанная с площадью 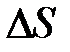 поверхности пленки.
поверхности пленки.
· Формула Лапласа, позволяющая определить избыточное давление для произвольной поверхности жидкости двоякой кривизны,
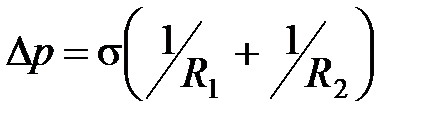 ,
,
где 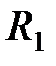 и
и 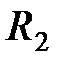 – радиусы кривизны двух взаимно перпендикулярных нормальных сечений поверхности жидкости; радиус кривизны положителен, если центр кривизны находится внутри жидкости (выпуклый мениск), и отрицателен, если центр кривизны вне жидкости (вогнутый мениск). Для сферической поверхности
– радиусы кривизны двух взаимно перпендикулярных нормальных сечений поверхности жидкости; радиус кривизны положителен, если центр кривизны находится внутри жидкости (выпуклый мениск), и отрицателен, если центр кривизны вне жидкости (вогнутый мениск). Для сферической поверхности
Δp = 2σ/R.
· Высота подъема жидкости в капиллярной трубке
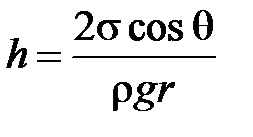 ,
,
где  – краевой угол;
– краевой угол; 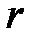 – радиус капилляра;
– радиус капилляра; 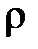 – плотность жидкости;
– плотность жидкости; 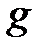 – ускорение свободного падения.
– ускорение свободного падения.
· Закон Дюлонга и Пти
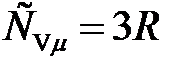 ,
,
где 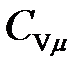 – молярная (атомная) теплоемкостьхимически простых твердых тел.
– молярная (атомная) теплоемкостьхимически простых твердых тел.
· Уравнение Клапейрона – Клаузиуса, позволяющее определить изменение температуры фазового перехода в зависимости от изменения давления при равновесно протекающем процессе:
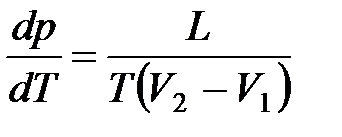 ,
,
где 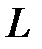 – теплота фазового перехода;
– теплота фазового перехода; 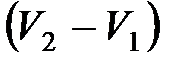 – изменение объема вещества при переходе его из первой фазы во вторую;
– изменение объема вещества при переходе его из первой фазы во вторую; 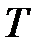 – температура перехода (процесс изотермический).
– температура перехода (процесс изотермический).
ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ
Электростатическое поле
· Закон Кулона
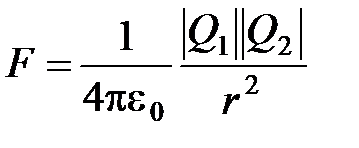 ,
,
где 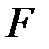 – сила взаимодействия двух точечных зарядов
– сила взаимодействия двух точечных зарядов 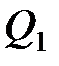 и
и 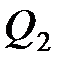 в вакууме;
в вакууме; 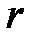 – расстояние между зарядами;
– расстояние между зарядами; 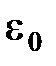 – электрическая постоянная, равная
– электрическая постоянная, равная 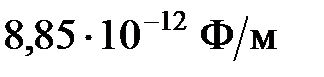 .
.
· Напряженность и потенциал электростатического поля
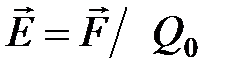 ,
, 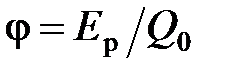 или
или 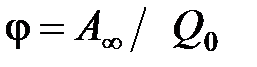 ,
,
где 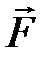 – сила, действующая на точечный положительный заряд
– сила, действующая на точечный положительный заряд 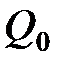 , помещенный в данную точку поля; Ep – потенциальная энергия заряда
, помещенный в данную точку поля; Ep – потенциальная энергия заряда 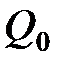 ;
; 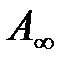 – работа перемещения заряда
– работа перемещения заряда 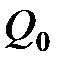 из данной точки поля за его пределы.
из данной точки поля за его пределы.
· Напряженность и потенциал электростатического поля точечного заряда 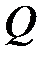 на расстоянии
на расстоянии 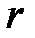 от заряда:
от заряда:
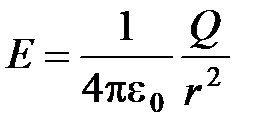 ,
, 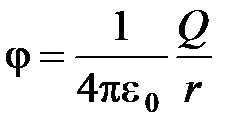 .
.
· Поток вектора напряженности сквозь площадку : 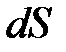
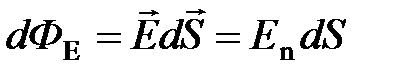 ,
,
где 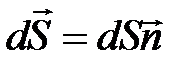 – вектор, модуль которого равен
– вектор, модуль которого равен 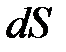 , а направление совпадает с единичной нормалью
, а направление совпадает с единичной нормалью 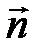 к площадке
к площадке 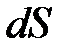 ;
; 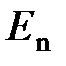 – проекция вектора
– проекция вектора 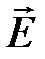 на нормаль
на нормаль 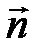 к площадке
к площадке 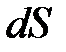 .
.
· Поток вектора напряженности через произвольную поверхность 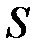 :
:
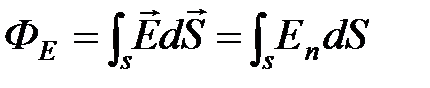 .
.
· Принцип суперпозиции (наложения) электростатических полей:
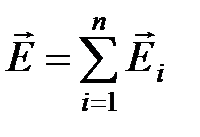 ;
; 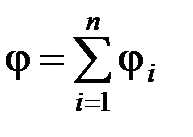 ,
,
где 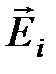 ,
, 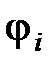 – соответственно напряженность и потенциал поля, создаваемого зарядом
– соответственно напряженность и потенциал поля, создаваемого зарядом 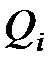 .
.
·
· Связь между напряженностью и потенциалом электростатического поля
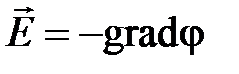 или
или 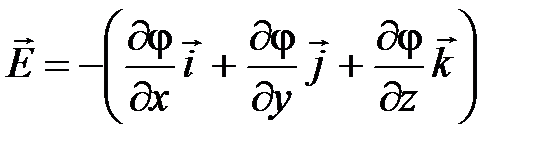 ,
,
где 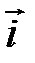 ,
,  ,
, 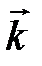 – единичные векторы координатных осей.
– единичные векторы координатных осей.
· В случае поля, обладающего центральной или осевой симметрией:
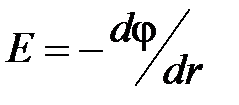 .
.
· Электрический момент диполя (дипольный момент):
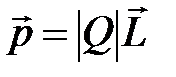 ,
,
где 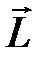 – плечо диполя.
– плечо диполя.
· Линейная, поверхностная и объемная плотности зарядов:
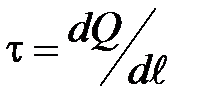 ;
; 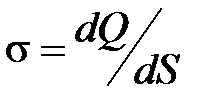 ;
; 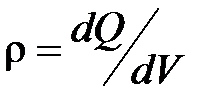 ,
,
т. е. соответственно заряд, приходящийся на единицу длины, поверхности и объема.
· Теорема Гаусса для электростатического поля в вакууме
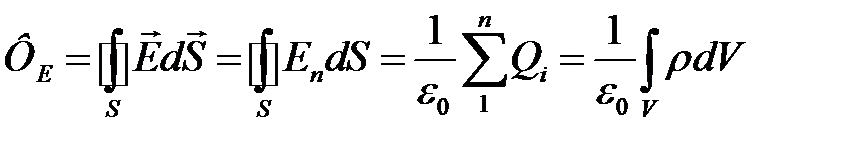 ,
,
где 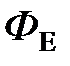 – поток вектора напряженности электростатического поля в вакууме;
– поток вектора напряженности электростатического поля в вакууме; 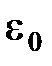 – электрическая постоянная;
– электрическая постоянная; 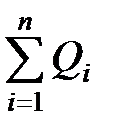 – алгебраическая сумма зарядов, заключенных внутри замкнутой поверхности
– алгебраическая сумма зарядов, заключенных внутри замкнутой поверхности 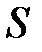 ;
; 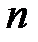 – число зарядов;
– число зарядов; 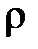 – объемная плотность зарядов.
– объемная плотность зарядов.
· Напряженность поля, создаваемого равномерно заряженной бесконечной плоскостью:
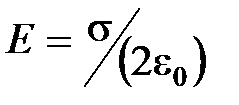 .
.
· Напряженность поля, создаваемого двумя бесконечными параллельными разноименно заряженными плоскостями:
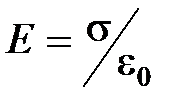 .
.
· Напряженность поля, создаваемого равномерно заряженной сферической поверхностью радиусом 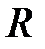 с общим зарядом
с общим зарядом 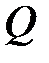 , на расстоянии
, на расстоянии 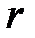 от центра сферы,
от центра сферы,
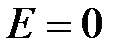 при
при 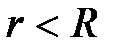 (внутри сферы);
(внутри сферы);
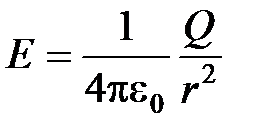 при
при 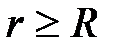 (вне сферы).
(вне сферы).
· Напряженность поля, создаваемого объемно заряженным шаром радиусом 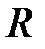 с общим зарядом
с общим зарядом 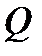 , на расстоянии
, на расстоянии 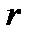 от центра шара:
от центра шара:
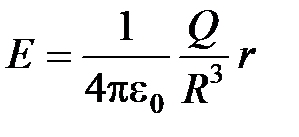 при
при 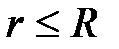 (внутри шара);
(внутри шара);
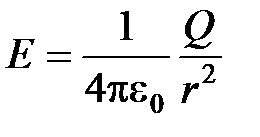 при
при 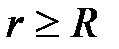 (вне шара).
(вне шара).
· Напряженность поля, создаваемого равномерно заряженным с линейной плотностью τ бесконечным цилиндром радиусом 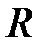 на расстоянии
на расстоянии 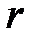 от оси цилиндра,
от оси цилиндра,
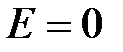 при
при 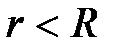 (внутри цилиндра);
(внутри цилиндра);
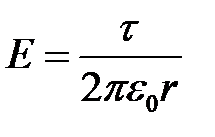 при
при 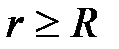 (вне цилиндра).
(вне цилиндра).
· Циркуляция вектора напряженности электростатического поля вдоль замкнутого контура
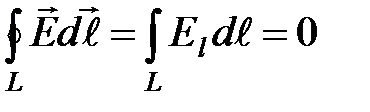 ,
,
где 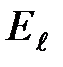 – проекция вектора
– проекция вектора 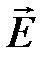 на направление элементарного перемещения
на направление элементарного перемещения 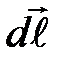 . Интегрирование производится по любому замкнутому пути
. Интегрирование производится по любому замкнутому пути 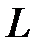 .
.
· Работа, совершаемая силами электростатического поля при перемещении заряда 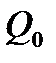 из точки 1 в точку 2,
из точки 1 в точку 2,
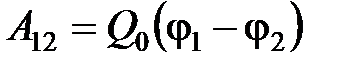 или
или 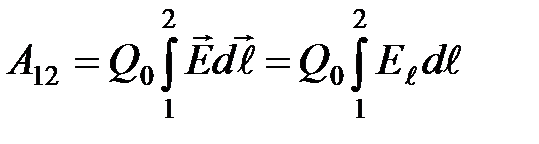
· Поляризованность диэлектрика:
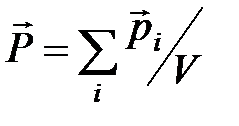 ,
,
где 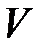 – объем диэлектрика;
– объем диэлектрика; 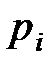 – дипольный момент
– дипольный момент 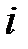 -й молекулы.
-й молекулы.
· Связь между поляризованностью диэлектрика и напряженностью электростатического поля:
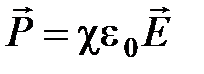 ,
,
где 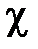 – диэлектрическая восприимчивость вещества.
– диэлектрическая восприимчивость вещества.
· Связь диэлектрической проницаемости 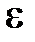 с диэлектрической восприимчивостью
с диэлектрической восприимчивостью 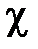 :
:
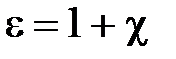 .
.
· Связь между напряженностью 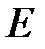 поля в диэлектрике и напряженностью
поля в диэлектрике и напряженностью 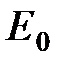 внешнего поля:
внешнего поля:
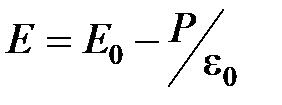 , или
, или 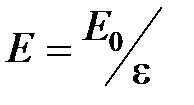 .
.
· Связь между векторами электрического смещения и напряженностью электростатического поля:
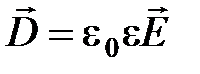 .
.
· Связь между 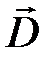 ,
, 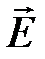 и
и 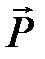 :
:
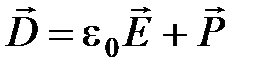 .
.
· Теорема Гаусса для электростатического поля в диэлектрике
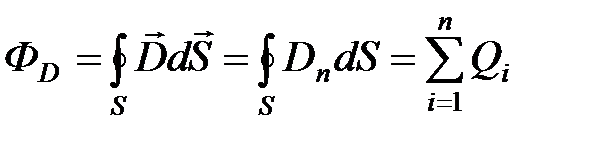
где 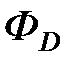 – поток вектора электростатического смещения;
– поток вектора электростатического смещения; 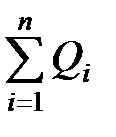 – алгебраическая сумма заключенных внутри замкнутой поверхности
– алгебраическая сумма заключенных внутри замкнутой поверхности 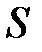 свободных электрических зарядов;
свободных электрических зарядов; 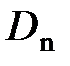 – проекция вектора
– проекция вектора 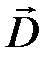 на нормаль
на нормаль 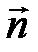 к площадке
к площадке 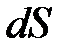 ;
; 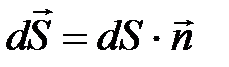 – вектор, модуль которого равен
– вектор, модуль которого равен 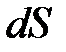 , а направление совпадает с нормалью
, а направление совпадает с нормалью 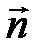 к площадке.
к площадке.
· Напряженность электростатического поля у поверхности проводника
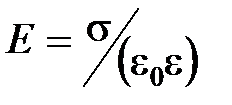 ,
,
где  – поверхностная плотность зарядов.
– поверхностная плотность зарядов.
· Электроемкость уединенного проводника
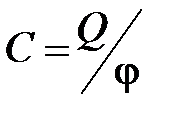 ,
,
где 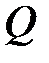 – заряд, сообщенный проводнику;
– заряд, сообщенный проводнику; 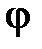 – потенциал проводника.
– потенциал проводника.
· Емкость плоского конденсатора:
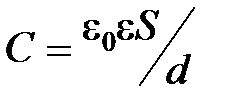 ,
,
где 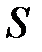 – площадь каждой пластины конденсатора;
– площадь каждой пластины конденсатора; 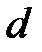 – расстояние между пластинами.
– расстояние между пластинами.
· Емкость цилиндрического конденсатора
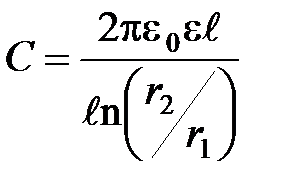 ,
,
где 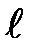 – длина обкладок конденсатора;
– длина обкладок конденсатора; 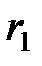 и
и 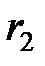 радиусы полых коаксиальных цилиндров.
радиусы полых коаксиальных цилиндров.
· Емкость сферического конденсатора
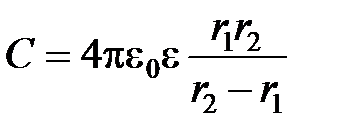 ,
,
где 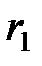 и
и 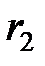 – радиусы концентрических сфер.
– радиусы концентрических сфер.
· Емкость системы конденсаторов при последовательном и параллельном соединениях:
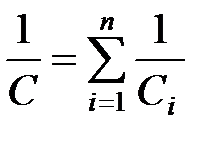 ,
, 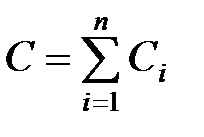 ,
,
где 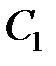 – емкость
– емкость 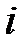 -го конденсатора;
-го конденсатора; 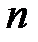 – число конденсаторов.
– число конденсаторов.
· Энергия уединенного заряженного проводника
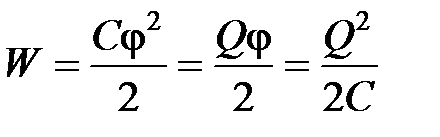 .
.
· Энергия взаимодействия системы точечных зарядов
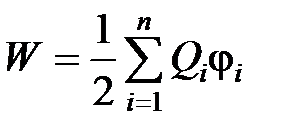 ,
,
где 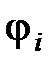 – потенциал, создаваемый в той точке, где находится заряд
– потенциал, создаваемый в той точке, где находится заряд 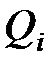 , всеми зарядами, кроме
, всеми зарядами, кроме 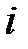 -го.
-го.
· Энергия заряженного конденсатора
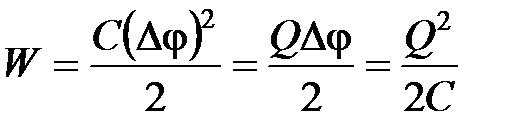 ,
,
где 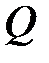 – заряд конденсатора;
– заряд конденсатора;  – его емкость;
– его емкость; 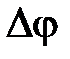 – разность потенциалов между обкладками.
– разность потенциалов между обкладками.
· Сила притяжения между двумя разноименно заряженными обкладками конденсатора:
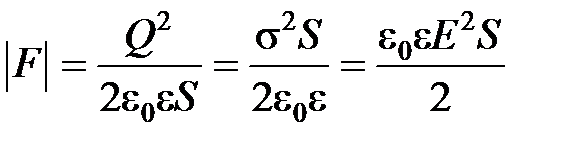 .
.
· Энергия электростатического поля плоского конденсатора
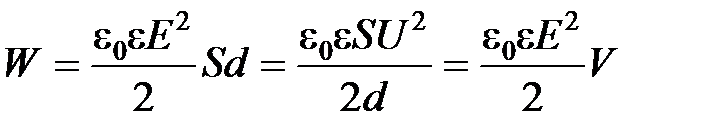 ,
,
где 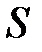 – площадь одной пластины;
– площадь одной пластины; 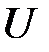 – разность потенциалов между пластинками;
– разность потенциалов между пластинками; 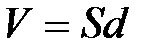 – объем конденсатора.
– объем конденсатора.
· Объемная плотность энергии
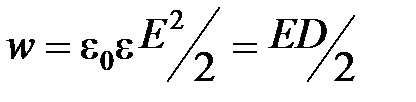 ,
,
где Е – напряженность электрического поля, 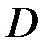 – электрическое смещение.
– электрическое смещение.
