Образование систематического кода

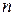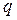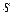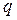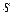Обычно для построения кодов необходимо знать длину кодовой комбинации , кратность обнаруживаемых ошибок , число исправляемых ошибок . Числа и задают минимально допустимое кодовое расстояние 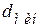, [Гуров, стр. 417].Для построения всевозможных кодовых комбинаций строится порождающая матрица (производящая матрица), состоящая из 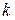строк и 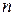столбцов и удовлетворяющая следующим условиям:

1. все исходные комбинации должны быть различны,

2. нулевая комбинация не должна входить в число исходных комбинаций,

3. исходные кодовые комбинации должны быть линейно независимыми,

4. каждая кодовая комбинация должна иметь вес не менее ,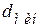

5. кодовое расстояние между любой парой исходных кодовых комбинаций должно быть не менее .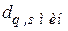

Подобранные определённым образом и удовлетворяющие приведённым условиям кодовые комбинации образуют матрицу, состоящую из 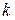строк и 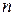столбцов. Полученная матрица называется производящей.

Если имеется кодовая комбинация, состоящая из 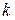символов, число всевозможных кодов равно 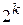. Их них выделяются 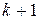кодовых комбинаций, остальные 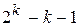комбинаций находятся как линейные комбинации строк, входящих в производящую матрицу.

Запишем производящую матрицу

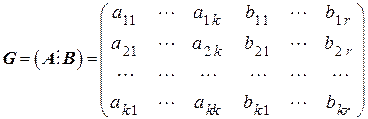. (5.9)

Как видно, матрица 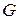состоит из двух частей – информационной подматрицы 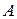размерности 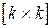и проверочной подматрицы 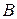размерности 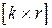. В число разрешённых кодовых комбинаций 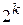входят кодовые комбинации, образующие единичную матрицу 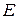размерности 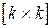. Заменим информационную часть матрицы 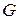единичной матрицей 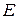и получим матрицу

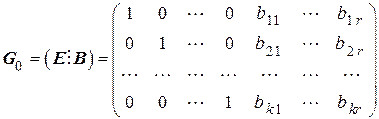, (5.10)

которая называется канонической формой порождающей матрицы.

Три исходных требования к порождающей матрице 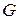выполняются автоматически. Выдвинем условия к строкам подматрицы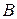

- число единиц в каждой строке не менее ,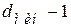

- кодовое расстояние между строками подматрицы 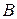должно быть не менее .

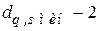Таким образом, удовлетворяются все требования, выдвинутые к матрице 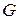. Зная информационную часть порождающей матрицы, можно на основе требований к канонической форме порождающей матрицы 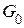найти проверочные символы 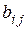. [Темников, стр. 145]

Обычно бывает известно количество передаваемых сообщений или количество информационных разрядов 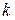, а также число обнаруживаемых или исправляемых ошибок. По ним определяется число символов 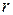, необходимых для проверочной части кода 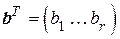. Из всего множества 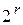кодов выбираются произвольно 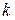кодов, удовлетворяющие условиям построения подматрицы 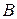в выражении (5.10) , и строки подматрицы 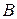заменяются выбранными кодами. В результате получается производящая матрица 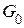. В дальнейшем производящая матрица 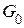используется как для построения проверочной части 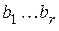кода 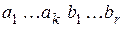, так и для обнаружения и исправления возникших ошибок.

Определим матрицу

,

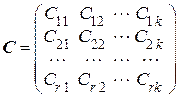элементы которой использованы в выражении (5.8), считая, что каноническая форма матрицы 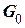известна, т.е. 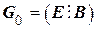. Из соотношения 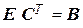получим .

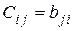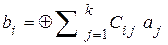
Определение проверочной части кода 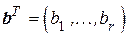. Положим, известна информационная часть кода 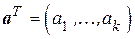. Воспользуемся определением систематического кода. Элементы 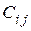в выражении (5.8) равны элементам 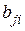матрицы 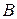, т.е. 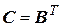. Тогда согласно (5.8)

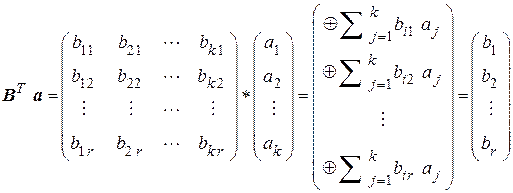. (5.11)

Полученные символы 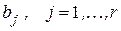, приписываются справа к информационной части кода. В результате будет построена кодовая комбинация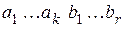

Обнаружение и исправление одиночной ошибки. Проверка на наличие или отсутствие ошибки и исправление ошибки основана на свойстве систематического кода, а именно – любая линейная комбинация кодов, входящих в производящую матрицу даёт также систематический код, Следовательно, достаточно построить алгоритм проверки для кодов производящей матрицы. Используем каноническое представление 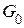производящей матрицы. Введем проверочную матрицу в виде канонической формы

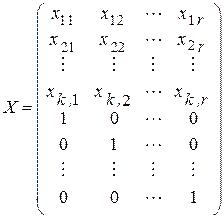, (5.12)

элементы которой 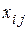необходимо определить.

Применим правило: произведение любой разрешённой неискажённой кодовой комбинации на проверочную матрицу 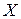должно быть равно кодовой комбинации с нулевыми значениями.

Следовательно, произведение канонической формы производящей матрицы на проверочную матрицу равно нулевой матрице:

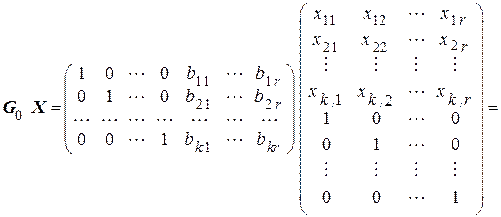
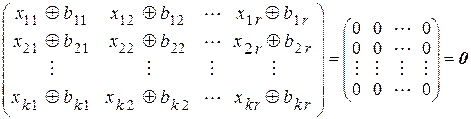= . (5.13)

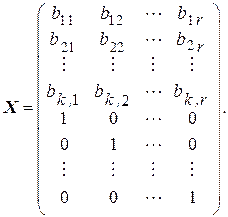Из соотношения (5.13) следует, что 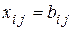, и каноническая форма проверочной матрицы имеет вид

Составим систему линейных уравнений для проверки наличия ошибки в принятой реализации.

Положим, 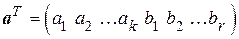- зарегистрированная кодовая комбинация.

Произведение зарегистрированной кодовой комбинация 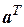на проверочную матрицу имеет вид

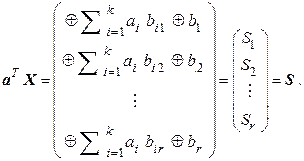(5.14)

Получили систему линейных уравнений для исправления однократной ошибки.

Если в принятой кодовой комбинации нет однократных ошибок, то вектор ошибок 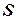равен нулю. Вектор 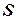называется синдромом ошибки (совокупностью симптомов) Синдром 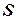не равен нулю, если в кодовой комбинации присутствуют ошибки.

Код однократной ошибки равен «1» в каком либо разряде и «0» во всех остальных 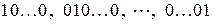. Код ошибки суммируется по модулю 2 с информационным символом и в результате получается искажённая кодовая комбинация

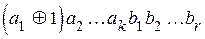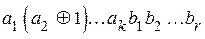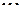или , или , или

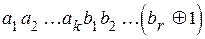и тогда вектор ошибок 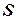не равен нулю.

Из приведённой записи искажённых кодовых комбинаций ясно, что каждой ошибочной кодовой комбинации соответствует свой вектор ошибки. По этому признаку в приёмнике инвертируется определённый разряд в принятой кодовой комбинации.

Существует другой способ исправления однократных ошибок. Для каждой разрешённой кодовой комбинации записываются множество кодов с однократной ошибкой. Если произошла однократная ошибка, принятая кодовая комбинация принадлежит одному из множеств, соответствующей одной разрешённой кодовой комбинации. По этому множеству определяется истинное значение кодовой комбинации. Однако этот метод требует большого объёма памяти.

Пример 5.2. Положим необходимо произвести кодирование пятиразрядных двоичных кодов с исправлением однократной ошибки, ( 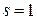). Записать производящую матрицу

1. Из неравенства (5.6) определим необходимое число разрядов 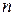и число проверочных символов .

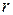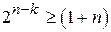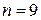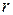, , = 4.

2. Из неравенства (5.3) определяется минимальное кодовое расстояние

.

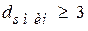3. Определяются требования к проверочной подматрице 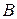канонической формы производящей матрицы 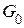(5.10).

3.1 Число единиц в кодовых последовательностях, входящих в подматрицу 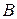должно быть не менее 2.

3.2 Кодовое расстояние между любыми двумя кодовыми последовательностями, входящими в подматрицу 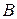, должно быть не менее 1.

4. Выпишем все четырёхразрядные коды, удовлетворяющие условиям 3.1 и 3.2:

0011, 0101, 0110, 0111, 1001, 1010, 1011, 1100, 1101, 1110, 1111.

5. Информационная часть производящей матрицы – единичная матрица размерности [5‰5]. Выберем произвольно пять кодов из пункта 4 и образуем каноническую форму 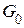производящей матрицы .

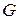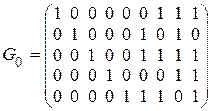6. Всего можно образовать 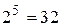пятиразрядных кода. Пять кодовых комбинаций уже использовано, нулевая комбинация известна. Остальные 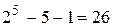комбинаций находятся как линейные комбинации строк, входящих в производящую матрицу. Например, возьмём 1-ю, 2-ю и 4-ю строки производящей матрицы 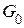и сложим их поразрядно по модулю 2. Результат сложения записан в последнюю строчку.

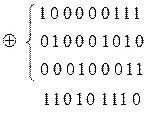7. Используя матрицу 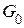, запишем каноническую форму проверочной матрицы X.

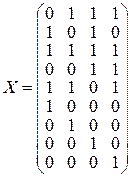8. На основе проверочной матрицы X и принятой кодовой комбинации 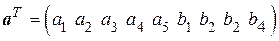составим систему проверочных уравнений, используя (5.14),

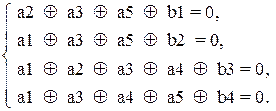(5.15)

Таблица 5.1

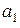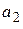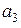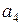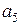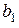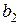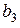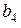Если принятая кодовая комбинация не содержит одиночной ошибки, то синдром S равен нулю. Определим синдромы ошибок для каждого символа кодовой комбинации. Например, синдром ошибки для символа 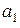получим, заменив символ 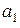во всех уравнениях (5.15) на «1»,а остальные символы на «0» и выполнив

сложение по модулю 2, получим код 0111, который соответствует синдрому 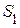, (Таблица 5.1). Точно также можно получить синдромы ошибок для других символов .

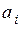1 Å 0 Å 0 Å 1=0 1 Å 0 Å 0 Å 1=0 1 Å 1 Å 0 Å 1 Å 1=0 1 Å 0 Å 1 Å 0 Å 0=0

Положим, принятая кодовая комбинация равна 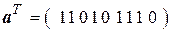. Подставим значения символов вектора 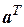в систему проверочных уравнений (5.15) и получим синдром ошибки S,равный нулю.

9. Введём однократную ошибку 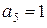в вектор -

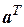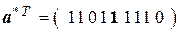. Во всех проверочных уравнениях символ 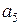изменяется на обратный символ. После подстановки символов вектора 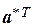в систему проверочных уравнений получим значение синдрома 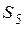= 1101.

1 Å 0 Å 1 Å 1=1 1 Å 0 Å 1 Å 1=1 1 Å 1 Å 0 Å 1 Å 1=0 1 Å 0 Å 1 Å 1 Å 0=1

Как известно, значение синдрома, не равное нулю, однозначно определяет номер разряда в кодовой комбинации. В приведённом примере пятый разряд в векторе 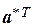следует изменить на обратный и получится первоначальный вектор .

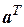Число синдромов, не равных нулю, равно числу разрядов принятой кодовой комбинации. Синдромы для символов кодовой комбинации 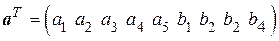имеют вид, приведённый в таблице 5.1.

Указанные синдромы сохраняются для любых кодовых комбинаций, полученных по построенной производящей матрице. Например, для кода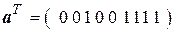

система проверочных уравнений примет вид

0 Å 1 Å 0 Å 1 = 0,

0 Å 1 Å 0 Å 1 = 0,

0 Å 0 Å 1 Å 0 Å 1 = 0 ,

0 Å 1 Å 0 Å 0 Å 1 = 0 .

Если произошла ошибка, скажем, в первом разряде, получим код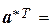

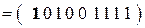. Система проверочных уравнений примет вид

0 Å 1 Å 0 Å 1 = 0,

1 Å 1 Å 0 Å 1 = 1,

1 Å 0 Å 1 Å 0 Å 1 = 1,

1 Å 1 Å 0 Å 0 Å 1 = 1.

Синдром 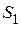= 0111 для первого разряда не изменился с изменением кодовой комбинации. С изменением производящей матрицы изменяются и синдромы.