Проекции углового ускорения при равноускоренном и равнозамедленном вращение; угловое ускорение, проекции углового ускорения при равноускоренном и равнозамедленном вращении.

(ИЛИ Кинематика вращательного движения: угловая скорость. Равномерное вращение. Угловое ускорение. Проекции углового ускорения при равноускоренном и равнозамедленном вращении.)

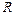Рассмотрим твердое тело, которое вращается вокруг неподвижной оси. Тогда отдельные точки этого тела бу­дут описывать окружности разных ра­диусов, центры которых лежат на оси вращения. Пусть некоторая точка дви­жется по окружности радиуса (рис. 6). Ее положение через промежуток времени 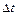; задается углом .

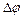Рис. 6 Рис. 7

Элементарные (бесконечно малые) повороты можно рассматривать как векторы (они обозначаются 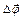или 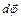). Модуль вектора 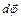равен углу поворота, а его направление совпадает с на­правлением поступательного движения острия винта, головка которого враща­ется в направлении движения точки по окружности, т. е. подчиняется правилу правого винта(см. рис. 6). Векторы, направления которых связываются с направлением вращения, называются псевдовекторами или аксиальными векторами. Эти векторы не имеют оп­ределенных точек приложения: они могут откладываться из любой точки оси вращения.

Угловой скоростьюназывается век­торная величина, определяемая первой производной угла поворота тела по вре­мени:

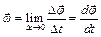
Вектор направлен вдоль оси вра­щения по правилу правого винта, т.е. так же, как и вектор 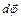(рис. 7). Единица измерения угловой скорости — радиан в секунду (рад/с).

Линейная скорость точки (см. рис. 6)

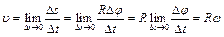
т.е. .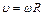

В векторном виде формулу для ли­нейной скорости можно написать как векторное произведение:

.

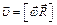При этом модуль векторного про­изведения, по определению, равен

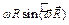, а направление совпадает с направлением поступательного движе­ния правого винта при его вращении от 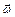к .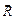

Если 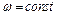, то вращение равно­мерное и его можно характеризовать периодом вращения Т — временем, за которое точка совершает один полный оборот, т. е. поворачивается на угол 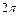. Так как промежутку времени 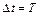со­ответствует 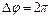, то 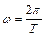, откуда .

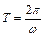Число полных оборотов, совершае­мых телом при равномерном его движе­нии по окружности в единицу времени, называется частотой вращения.

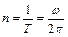, откуда .

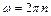Угловым ускорением называется Векторная Величина, определяемая пер­вой производной угловой скорости по времени: .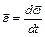

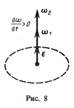
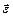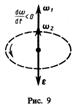
При вращении тела вокруг непод­вижной оси вектор углового ускорения направлен вдоль оси вращения в сторо­ну вектора элементарного приращения угловой скорости. При ускоренном движении вектор сонаправлен вектору 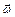(рис. 8), при замедленном – противонаправлен ему (рис. 9).

Тангенциальная составляющая ускорения .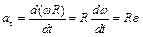

Нормальная составляющая ускорения .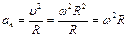

Таким образом, связь между линей­ными (длина пути 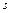, пройденного точ­кой по дуге окружности радиусом 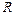, ли­нейная скорость 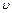, тангенциальное уско­рение 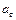, нормальное ускорение 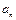) и угловыми величинами (угол поворота 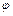, угловая скорость 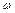, угловое ускорение 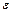) выражается следующими формулами: , , , .

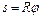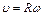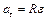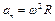В случае равномерного движения точки по окружности ( )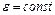

, ,

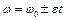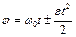где 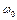– начальная угловая скорость.

Закон термодинамики. Тепловые машины и их КПД. Цикл Карно и его КПД. Абсолютная температура. Определение и свойства энтропии. Энтропия идеального газа. Энтропия как функция состояния.

Термодинамика – это раздел физики, изучающий соотношения и превращения теплоты и других форм энергии. В термодинамике имеют дело не с отдельными молекулами, а с макроскопическими телами, состоящими из огромного числа частиц. Эти тела называются термодинамическими системами. В термодинамике тепловые явления описываются макроскопическими величинами — давление, температура, объём, …, которые не применимы к отдельным молекулам и атомам.

Первый закон термодинамики: теплота, сообщаемая системе, расходуется на изменение ее внутренней энергии и на совершение ею работы против внешних сил, (ИЛИизменение внутренней энергии системы при переходе ее из одного состояния в другое равно сумме работы внешних сил и количества теплоты, переданного системе): .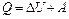

Это выражение в дифференциальной форме будет выглядеть так: 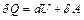, где 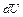– бесконечно малое изменение внутренней энергии системы, 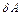– элементарная работа, 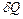– бесконечно малое количество теплоты. В этот выражении 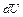является полным дифференциалом, а 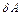и 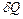таковыми не являются.

Второй закон термодинамики указывает направление возможных энергетических превращений и тем самым выражает необратимость процессов в природе. Он был установлен путем непосредственного обобщения опыт­ных фактов.

Есть несколько формулировок второго закона термодина­мики, которые, несмотря на внешнее различие, выражают в сущности одно и то же и поэтому равноценны. Немецкий уче­ный Р. Клаузиус сформулировал этот закон так:

невозможно перевести тепло от более холодной системы к более горячей при отсутствии одновременных изменений в обеих системах или окружающих телах.

Здесь констатируется опытный факт определенной направ­ленности теплопередачи: теплота сама собой переходит всегда от горячих тел к холодным. Правда, в холодильных установ­ках осуществляется теплопередача от холодного тела к более теплому, но эта передача связана с другими изменениями: ох­лаждение достигается за счет работы.

Другая формулировка принадлежит английскому ученому У. Кельвину:

невозможно осуществить такой периодический процесс, единственным результатом которого было бы получение ра­боты за счет теплоты, взятой от одного источника.

Здесь опять констатируются и уточняются опытные факты. Если, например, паровая машина совершает работу за счет теплоты, полученной от парового котла, то при этом совер­шаемая работа не является единственным результатом про­цесса, так как часть теплоты обязательно уходит в атмосферу вместе с отработанным паром. То же самое относится к двига­телям внутреннего сгорания и вообще ко всем тепловым дви­гателям. Иначе говоря, ни один тепловой двигатель не может иметь коэффициент полезного действия, равный единице. Под коэффициентом полезного действия 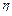теплового двигателя понимают отношение совершенной машиной работы А к количеству полученной для этой цели теплоты : .

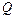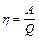Существуют тепловые двигатели и холодильные машины. Тепловые двигатели – это периодически действующие двигатели, совершающие работу за счет полученной из вне теплоты. Холодильные машины – это периодически действующие установки, в которых за счет работы внешних сил теплота переносится к телу с более высокой температурой. В тепловых двигателях используется прямой цикл (если за цикл совершается положительная работа, то он называется прямым циклом), а в холодильных машинах – обратный цикл (если за цикл совершается отрицательная работа, то он называется обратным циклом). Циклом (или круговым процессом) называют процесс, при котором система, пройдя через ряд состояний, возвращается в исходное.

В результате кругового процесса система возвращается в исходное состояние и, следовательно, полное изменение внутренней энергии газа равно нулю. Поэтому первое начало термодинамики: 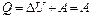(1), т.е. работа, совершаемая за цикл, равна количеству полученной из вне теплоты. Однако в результате кругового процесса система может теплоту как получать, так и отдавать, поэтому: 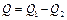, где 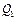– количество теплоты, полученной системой, – количество теплоты, отданное системой. Поэтому термодинамический коэффициент полезного действия для кругового процесса: 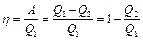(2)

Из формулировки второго начала термодинамики по Кельвину следует, что вечный двигатель второго рода — периодически действующий двигатель, совершающий работу за счет охлажде­ния одного источника теплоты, — не­возможен. Для иллюстрации этого по­ложения рассмотрим работу теплового двигателя (исторически второе начало термодинамики и возникло из анализа работы тепловых двигателей).

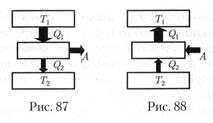Принцип действия теплового двига­теля приведен на рис. 87. От термоста­та (Термодинамическая система, которая мо­жет обмениваться теплотой с телами без изме­нения температуры.) с более высокой температурой 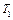на­зываемого нагревателем, за цикл отби­рается количество теплоты 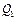, а термо­стату с более низкой температурой 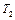, называемому холодильником, за цикл передается количество теплоты 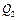при этом совершается работа .

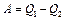Чтобы термический коэффициент полезного действия теплового двигате­ля был равен 1, необходимо вы­полнение условия 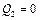, т.е. тепловой двигатель должен был бы иметь один источник теплоты. Однако, согласно Карно, для работы теплового двигате­ля необходимо не менее двух источни­ков теплоты с различными температу­рами, иначе это противоречило бы вто­рому началу термодинамики.

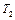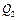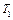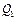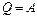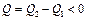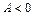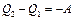Процесс, обратный происходящему в тепловом двигателе, используется в холодильной машине, принцип дей­ствия которой представлен на рис. 88. Системой за цикл от термостата с бо­лее низкой температурой отнимает­ся количество теплоты и отдается за цикл термостату с более высокой тем­пературой , количество теплоты . Для кругового процесса, согласно (1), , но, по условию, , поэтому и или 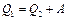, т.е. количество теплоты 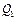отданное системой источнику теплоты при более высокой температуре 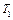, больше количества теплоты 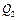, полу­ченного от источника теплоты при бо­лее низкой температуре 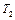, на величину работы, совершенной над системой. Следовательно, без совершения работы нельзя отбирать теплоту от менее на­гретого тела и отдавать ее более нагре­тому. Это утверждение есть не что иное, как второе начало термодинами­ки в формулировке Клаузиуса.

Однако второе начало термодинами­ки не следует представлять так, что оно совсем запрещает переход теплоты от менее нагретого тела к более нагрето­му. Ведь именно такой переход осуще­ствляется в холодильной машине. Но при этом надо помнить, что внешние силы совершают работу над системой, т. е. этот переход не является единственным результатом процесса.

Основываясь на втором начале термодинамики, Карно ввел теорему, носящую теперь его имя: Из всех периодически действующих тепловых машин, имеющих одинако­вые температуры нагревателей ( 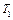) и холодильников ( 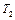), наибольшим КПД обладают обратимые машины; при этом КПД обратимых машин, работающих при одинаковых температурах нагрева­телей ( 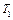) и холодильников ( 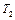), рав­ны друг другу и не зависят от природы рабочего тела (тела, совершающего кру­говой процесс и обменивающегося энергией с другими телами), а опреде­ляются только температурами нагрева­теля и холодильника.

Из всевозможных круговых процес­сов важное значение в термодинамике имеет цикл Карно — цикл, состоящий из четырех последовательных обрати­мых процессов: изотермического рас­ширения, адиабатного расширения, изотермического сжатия и адиабатно­го сжатия.

Прямой цикл Карно изображен на рис. 89, где изотермические расширение и сжатие заданы соответственно кривы­ми 1 — 2 и З — 4, а адиабатные расшире­ние и сжатие — кривыми 2 — З и 4 — 1. При изотермическом процессе 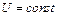, поэтому количество теплоты 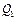, полученное газом от нагре­вателя, равно работе расширения 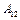, совершаемой газом при переходе из со­стояния 1 в состояние 2: 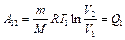. (3)

При адиабатном расширении 2 – 3 теплообмен теплообмен с окружающей средой отсутствует и работа расширения 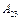со­вершается за счет изменения внутрен­ней энергии: 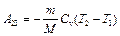. Количество теплоты 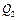отданное газом холодильнику при изотермическом сжатии, равно работе сжатия 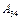: 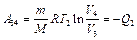. (4)

Работа адиабатического сжатия : .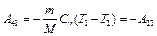

Работа, совершаемая в результате кругового процесса: 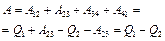, и, как можно показать, определяется площадью, заштрихованной на рис. 89.

Термодинамический КПД цикла Карно, согласно (2), .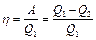

Применив уравнение 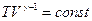для адиабат 2 – 3 и 4 – 1, получим: 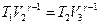, , 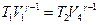откуда: 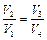. (5)

Подставляя (3) и (4) в формулу (2) и учитывая (5), получаем:

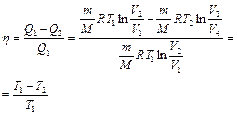(6)

т. е. для цикла Карно КПД действитель­но определяется только температурами нагревателя и холодильника (доказа­тельство теоремы Карно). Для повыше­ния КПД необходимо увеличивать раз­ность температур нагревателя и холо­дильника.

Обратный цикл Карно положен в основу действия тепловых насосов. В отличие от холодильных машин теп­ловые насосы должны как можно боль­ше тепловой энергии отдавать горяче­му телу, например системе отопления. Часть этой энергии отбирается от окру­жающей среды с более низкой темпера­турой, а часть получается за счет механической работы, производимой, на­пример, компрессором.

Теорема Карно послужила основа­нием для установления термодинами­ческой шкалы температур. Сравнив левую и правую части формулы (6), получим

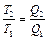(7) , т. е. для сравнения температур 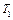и 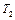двух тел необходимо осуществить цикл Карно, в котором одно тело использу­ется в качестве нагревателя, другое — как холодильник. Из равенства (7) видно, что отношение температур тел равно отношению отданного в этом цикле количества теплоты к получен­ному. Согласно теореме Карно, хими­ческий состав рабочего тела не влияет на результаты сравнения температур, поэтому такая термодинамическая шка­ла не связана со свойствами какого-то определенного термометрического тела. Отметим, что практически таким образом сравнивать температуры труд­но, так как реальные термодинамиче­ские процессы, как уже указывалось, являются необратимыми.

Понятие энтропии введено в 1865 г. Р. Клаузиусом. Для выяснения физи­ческого содержания этого понятия рас­сматривают отношение теплоты 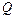, по­лученной телом в изотермическом про­цессе, к температуре 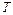теплоотдающего тела, называемое приведенным ко­личеством теплоты.

Приведенное количество теплоты, сообщаемое телу на бесконечно малом участке процесса, равно 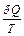. Строгий теоретический анализ показывает, что приведенное количество теплоты, сооб­щаемое телу в любом обратимом круго­вом процессе, равно .

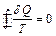Из равенства нулю интеграла, взятого по замкнутому контуру, следу­ет, что подынтегральное выражение 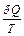есть полный дифференциал неко­торой функции, которая определяется только состоянием системы и не зави­сит от пути, каким система пришла в это состояние. Таким образом, 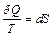. (8)

Функция состояния, дифференциалом которой является 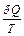, называется энтропией и обозначается .

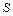Из формулы (8) следует, что для обратимых процессов изменение энтро­пии 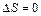. (9)

В термодинамике доказывается, что энтропия системы, совершающей нео­братимый цикл, возрастает: 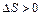. (10)

Выражения (9) и (10) относят­ся только к замкнутым системам, если же система обменивается теплотой с внешней средой, то ее энтропия может вести себя любым образом. Соотноше­ния (9) и (10) можно представить в виде неравенства Клаузиуса

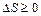, т.е. энтропия замкнутой системы мо­жет либо возрастать (в случае необра­тимых процессов), либо оставаться по­стоянной (в случае обратимых процес­сов).

Если система совершает равновес­ный переход из состояния 1 в состоя­ние 2, то, согласно (8), изменение эн­тропии 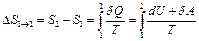(11), где подынтегральное выражение и пределы интегрирования определяются через величины, характеризующие исследуемый процесс. Энтропия определяет­ся с точностью до аддитивной посто­янной.

Значение постоянной, с которой определяется энтропия, не играет роли, так как физический смысл имеет не сама энтропия, а разность энтропии.

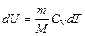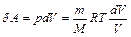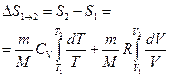Исходя из выражения (11), найдем изменение энтропии в процессах идеального газа. Так как , , то или 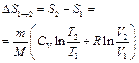(12) , т.е. изменение энтропии 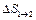идеального газа при переходе его из состоя­ния 1 в состояние 2 не зависит от вида процесса перехода .

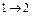Так как для адиабатного процесса 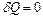, то 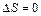и, следовательно, 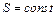, т. е. адиабатный обратимый процесс протекает при постоянной эн­тропии. Поэтому его часто называют изоэнтропийным процессом. Из фор­мулы (12) следует, что при изотермическом процессе ( 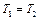): 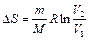; при изохорном процессе ( ): .

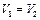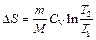Энтропия обладает свойством аддитивности: энтропия системы равна сумме энтропии тел, входящих в систему. Свойством аддитивности обладают также внутренняя энергия, масса, объем (температура и давление таким свойством не обладают).