Непрерывный канал передачи информации

Непрерывный канал передачи информации описывается одномерными и двумерными плотностями распределений вероятностей. Чтобы записать количество взаимной информации между входом и выходом канала связи, используем дискретное представление информации, а затем прейдем к непрерывным величинам.

Совместная вероятность появления символа 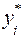на входе канала и символа 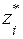на выходе канала равна

,

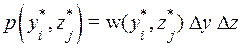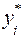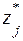где и -значения y и z, удовлетворяющие условиям 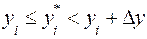, , 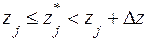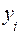и 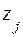- границы i-го и j-го интервалов квантования соответственно для y и z

Вероятность появления символа 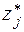на выходе канала при условии, что на вход подан символ 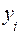, равна

.

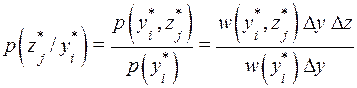Количество информации, содержащееся в символе 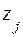, равно

.

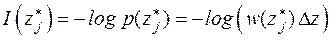Условное количество информации, содержащееся в элементе 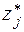, если на вход канала подаётся элемент ансамбля 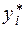, равно

.

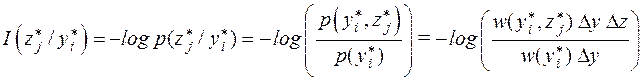Тогда количество информации, содержащееся в элементе 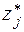относительно элемента 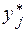, равно

.

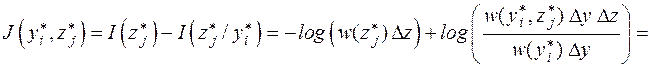
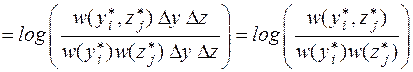Как видно из последнего выражения, интервалы квантования 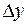и 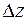не влияют на количество информации, содержащееся в элементе 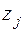относительно элемента .

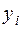Количество взаимной информации, содержащееся в ансамбле 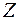относительно ансамбля 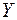, равно

.

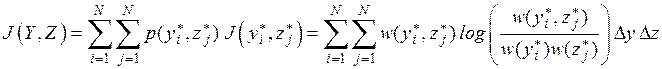Осуществляя в предыдущем выражении предельный переход 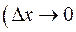, , 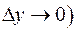получим интегральное представление количества взаимной информации, содержащееся в непрерывном ансамбле 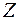относительно непрерывного ансамбля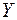

=

.

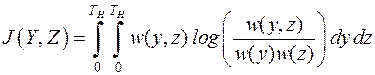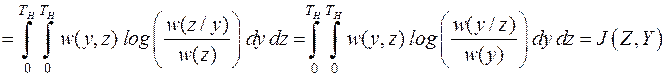Количество взаимной информации, содержащееся в ансамбле 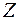относительно ансамбля 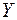, равно количеству взаимной информации, содержащееся в ансамбле 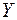относительно ансамбля .

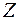Выразим количество взаимной информации 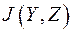через энтропию ассамблей Y и Z. Для этого используем предыдущую формулу

,

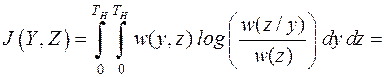
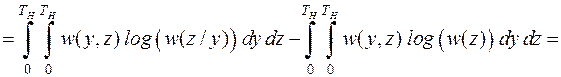
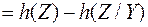где 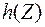- дифференциальная энтропия на один отсчёт процесса ,

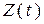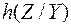- условная дифференциальная энтропия на один отсчёт процесса 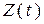при известном отсчёте .

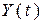Точно так же можно показать, взаимная информация равна

,

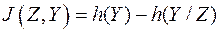
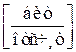где 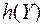- дифференциальная энтропия на один отсчёт процесса ,

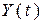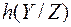- условная дифференциальная энтропия на один отсчёт процесса 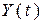при известном отсчёте 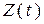называется ненадёжностью канала связи.

Рассмотрим 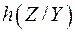- энтропию помехи в непрерывном канале связи. Сигналы на входе и выходе канала связи и помеха описываются линейной зависимостью 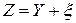, в которой каждая составляющая является непрерывной случайной величиной со своей плотностью распределения вероятности. Условная энтропия 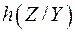имеет вид:

.

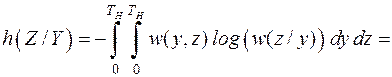
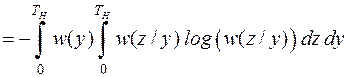Положим, плотность распределения вероятности шума известна и равна 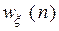. В условной плотности вероятности 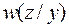величина y считается известной. Тогда случайная величина 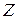при известной величине y зависит только от шума и имеет место 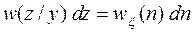, откуда получим

.

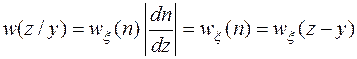Из этого выражения видно, что условная плотность 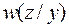зависит только от шума. В результате получим

,

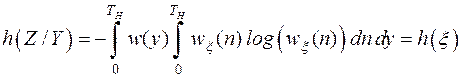
т.е. условная энтропия на один отсчёт 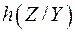равна энтропии шума 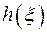на один отсчёт.

2.3.3 Эпсилон-энтропия (ε-энтропия)

Наличие помехи в канале связи ухудшает качество восстанавливаемого сигнала. Возникает вопрос, до какой степени можно допустить искажение сигнала помехой, чтобы можно было сказать, сигнал, поступивший в канал связи и вышедший из канала связи идентичны Критерии отождествления двух сигналов могут быть самыми различными. Необходимо ввести расстояние 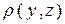между элементами ансамбле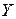й и 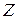. Мерой идентичности ансамбле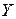й и 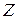наиболее часто берут математическое ожидание квадрата расстояния между элементами ансамбле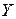й и :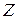

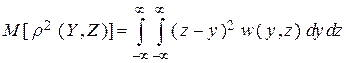
В качестве критерия «сходства» ансамбле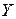й и 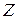примем выполнение неравенства

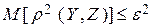(2.21)

где 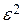- заранее заданная допустимая мера отклонения «сходства» ансамбле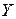й и .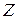

Заданную меру «сходства» 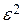необходимо обеспечить при минимальном количестве меры информации 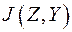. Ввиду того, что

,

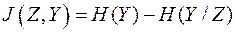a 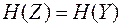при отсутствии шума, то необходимо минимизировать 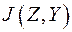по всем возможным распределениям плотности вероятности .

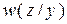Минимальное значение меры информации 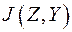при выполнении условия 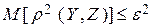называется эпсилон-энтропией (ε-энтропия) непрерывного ансамбля

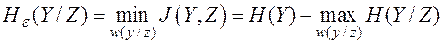.(2.22)

Понятие 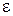-энтропия введено Колмогоровым А.Н. [Колмогоров А. Н. Теория информации и теория алгоритмов.— М.: Наука, 1987.-304 с.(стр.46)

Если на входе канала связи мощность сигнала ограничена величиной 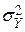, значения сигнала находятся в интервале 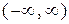, то энтропия 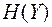не превышает энтропию нормального закона распределения вероятности. Энтропия нормального закона распределения вероятности равна 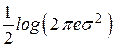. Условная энтропия 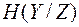зависит только от шума и принимает максимальное значение 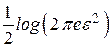при нормальном распределении шума мощностью, не превышающей 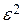. Учитывая значения безусловной и условной энтропий, получим

.

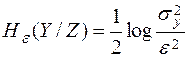
Положим, источник генерирует сообщения со скоростью [ ].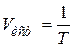

Тогда ε-призводительностьюисточника сообщений называется величина

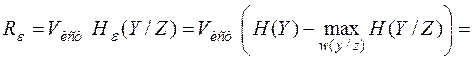
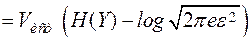
. (2.23)

Если учесть, что интервал дискретизации 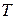есть величина обратная полосе частот, занимаемая сигналом, то, согласно теореме Котельникова, получим

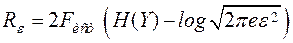
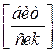, (2.24)

где 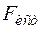- полоса частот, занимаемая сигналом источника, приходящаяся на один отсчёт.

Максимальная ε-призводительностьисточника сообщений будет тогда, когда значения сигнала 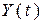распределены по нормальному закону с известной дисперсией ,

,

.

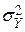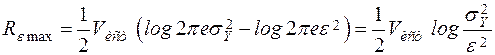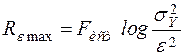Формулы (2.23) и (2.24) показывают, с какой скоростью можно генерировать информацию, чтобы восстановить сообщения с погрешностью, не превышающей 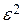.