Вероятность обнаружения частицы

По аналогии со светом вероятность обнаружения частицы в момент t в единичном интервале около точки x, или плотность вероятности, равна

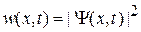. (1.14)

Вероятность обнаружения частицы в интервале dx

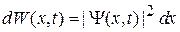. (1.15)

Вероятность найти частицу во всем пространстве равна единице и выполняется условие нормировки

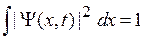. (1.16)

Квантование Бора–Зоммерфельда

В максимуме интерференции волна усиливается и увеличивается вероятность обнаружения частицы, пропорциональная квадрату модуля волны. Условие максимума интерференции для разности хода двух волн от точки их расхождения до точки наложения (1.3)

,

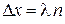где n – число длин волн, укладывающихся на протяжении 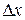, обеспечивает наибольшую вероятность обнаружения частицы. Точки максимума интерференции дают траекторию частицы. Учитывая (1.13)

,

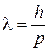получаем условие обнаружения частицы

.

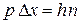Результат обобщаем на случай трехмерной замкнутой траектории с элементом 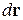, когда импульс изменяется вдоль траектории. Получаем условие квантование Бора–Зоммерфельда

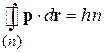, (1.17)

где

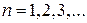– квантовое число, или номер траектории. Это число показывает сколько раз длина волны де Бройля укладывается на протяжении траектории;

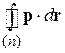– объем фазового пространства 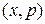одномерного движения, ограниченный траекторией частицы и занятый n состояниями.

Следовательно, квантовое состояние одномерного движения занимает в фазовом пространстве объем, равный h. На этом результате основана статистическая физика.

Формула (1.17) применима тольков квазиклассическом приближении, когда существует траектория частицы, т. е. длина волны гораздо меньше характерного размера траектории r. С учетом (1.13)

,

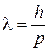и (1.17) получаем условие применимости (1.17)

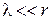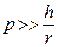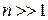, , . (1.18)

Полуклассическая теория неприменима для системы с характерным размером, сравнимым с длиной волны де Бройля, когда отсутствует понятие траектории частицы.

ПРИМЕР

В одномерной прямоугольной потенциальной яме шириной a с абсолютно непроницаемыми стенками находится частица массой m. Классическая физика не ограничивает энергию частицы в яме. Получим допустимые значения энергии и импульса частицы, используя квантование Бора–Зоммерфельда.

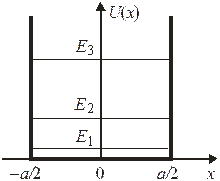
Частица с полной энергией 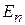внутри ямы при 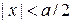имеет импульс

.

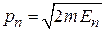Из условия квантования (1.17)

,

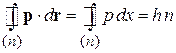где учтено, что импульс р направлен вдоль участка траектории 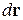, и эти вектора параллельны оси x. С учетом движения вправо и влево, находим:

,

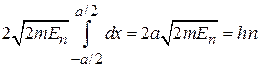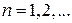
Получаем дискретный спектр энергии и модуля импульса

,

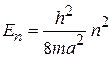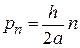. (П.1.3)

Чем уже яма и меньше масса частицы, тем выше уровень энергии и больше расстояние между соседними уровнями.

Длина волны де Бройля на уровне n

,

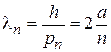тогда

.

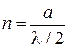Номер состояния равен числу полуволн, укладывающихся на ширине ямы.

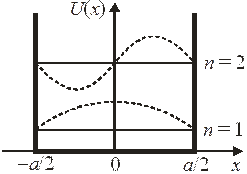
Для основного состояния 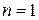с минимальной энергией из (П.1.3) получаем

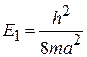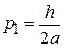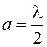, , . (П.1.4)

Энергия частицы в яме не может быть меньше этого значения.

Для электрона в потенциальной яме макроскопической ширины 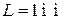находим

.

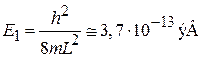Тепловая энергия kT такой величины достигается при температуре 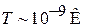. При нормальной температуре квантование энергии в яме несущественно. Для частицы в макроскопическом объеме квантование энергии поступательного движения несущественно при не слишком низкой температуре. В результате примена классическая физика.

Для микроразмера L = 1 нм получаем 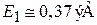, что превышает тепловую энергию 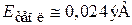при нормальной температуре. Следовательно, для частицы в микроскопическом объеме квантование энергии поступательного движения существенно при любой температуре. Классическая теория не применима для микро и наносистем.