Теория метода и вывод рабочей формулы

Лабораторная работа ФПО-10.

Изучение интерференции лазерного света в толстой стеклянной пластинке. Полосы равного наклона. Определение толщины плоскопараллельной стеклянной пластины по интерференционным кольцам. Определение длины волны лазерного света.

Цель и метод работы

1. Изучение интерференции красного лазерного света полупроводникового или гелий-неонового лазера.

2. Определение положения темных колец в интерференционной картине для различных значений расстояния L от пластины до плоскости наблюдения.

3. Проверка зависимости х_т = x_m(m,L).

4. Определение величины толщины стеклянной пластины, если известна длина излучения лазера, либо определение длины излучения лазера при заданной толщине пластины.

Основные теоретические положения

Интерференция света рассматривалась в лабораторной работе №4 «Интерференция. Бипризма Френеля». Мы продолжим изучение интерференционных явлений на примере интерференции света в толстой стеклянной пластинке при освещении ее расходящейся сферической монохроматической волной. В плоскости наблюдения происходит наложение волн отразившихся от передней и от задней поверхности пластинки. При наложении сферических волн в плоскости наблюдения возникает интерференционная картина в виде системы интерференционных колец - полос равного наклона (в отличие от колец Ньютона - колец равной толщины). Возможность возникновения интерференционной картины связано с большой когерентностью лазерного излучения. Интерференционная картина возникает, когда длина когерентности света больше разности хода интерферирующих волн.

Если плоскопараллельная стеклянная пластина освещена точечным источником S квазимонохроматического света, то в любую точку наблюдения Р, находящуюся с той же стороны, что и источник S, приходят две волны: одна - отразившаяся от передней поверхности пластины, и другая, отразившаяся от задней ее поверхности. Интерферируя, эти волны образуют не локализованную интерференционную картину. Из соображений симметрии понятно, что в плоскостях, параллельных пластине, интерференционные полосы имеют вид колец. Видность этих полос уменьшается при увеличении размеров источника в направлении перпендикулярном к плоскости пластины.

В случае точечного монохроматического источника света каждая точка пространства характеризуется вполне определенной разностью хода приходящих в нее отраженных волн. Поэтому для монохроматического когерентного источника света устойчивая интерференция должна наблюдаться в каждой точке пространства. Про соответствующие полосы интерференции говорят, что они не локализованы (или локализованы всюду).

Мы ограничились интерференцией только двух волн, пренебрегая при этом многократными переотражениями. Это приближение справедливо, когда коэффициент отражения невелик. Например, для стекла (п = 1,51) интенсивности волн, возникающих при однократном отражении от одной и другой плоскости почти одинаковы, а последующие переотражения уменьшают интенсивность в сто и более раз. Поэтому последующие отражения можно не принимать во внимание. Приведенные далее соотношения описывают интерференцию в толстой стеклянной пластине как двухлучевую интерференцию.

Теория метода и вывод рабочей формулы

В эксперименте изучается интерференция лазерного света. Как ясно из схемы опыта (рис.1), луч с помощью линзы Л собирается в фокусную точку S. Это - точечный источник монохроматического излучения. Свет от точки S пройдя через небольшое отверстие в экране, распространяется в виде сферической волны и падает на пластину П. Стеклянная пластина П расположена перпендикулярно к лучу лазера. Экран наблюдения Э находится в фокальной плоскости линзы Л, на расстоянии L от пластины. Плоскость экрана параллельна плоскости пластины П.

Защитный экран Э₂

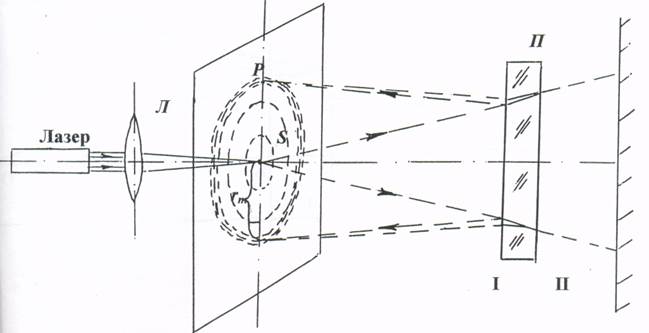
Экран наблюдения Э₁

Рис. 1

Итак, на экран падают две сферические волны, возникающие при отражении от передней и задней поверхности пластины. Разница между радиусами AR этих двух сферических волн в точке наблюдения Р определяется толщиной пластины h и коэффициентом преломления материала п. Интерференционная картина имеет вид концентрических темных и светлых колец (см.рис.2).

Рис. 2

Для описания картины интерференции определим радиусы колец в картине. Ход лучей при отражении от толстой стеклянной пластины показан на рис.3.

rm   S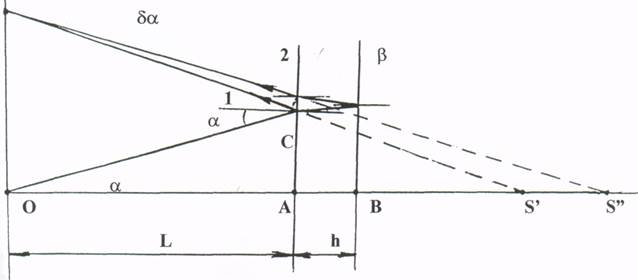

Рис. 3

Разность хода волн 1 и 2 (см.рис.З) приходящих к m-му кольцу (в точку r_m на рисунке) равна :

А = 2hnсоs b (1)

Можно полагать, что эти волны излучаются мнимыми точками 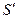и S" -изображениями источника S в передней и задней поверхностях пластины.

При условии D= тl кольцо порядка т оказывается темным, так как как к геометрической разности хода Dнеобходимо добавить еще 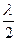и учесть, таким образом, изменение фазы волны 1 на p при отражении от передней поверхности пластины.

Полагаем, что L, велико: L » h, угол падения α -мал, δα,< < α .

Будем полагать для простоты, что центральной точке Отакже соответствует условие минимума, т.е. разность хода D₀ = 2hn = т_оl (т.е. точке Она экране наблюдения соответствует порядок интерференции т_о). Тогда m-му темному кольцу радиуса r_m отвечает порядок интерференции т_о — т и разность хода D = (т_о — т)l. Как видно из рис.3.

r_m = 2Ltga = 2La = 2Lnb (2 )

(b - угол преломления в пластинке, связанный с углом падения α законом преломления )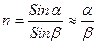

Мы получаем D₀ - D = 2hn (1-сosb) = тl или 2hnb ²= тl (так как 1 - сosb » 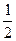b ²). Используя (2), находим b ² = 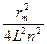. Окончательно, для

для радиуса m-ого темного кольца имеем:

r_m = 2L 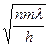(3)