Флуктуации аддитивных величин.

Величина 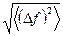называется средней квадратичной флуктуацией величины 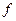. Эта величина как раз характеризует в среднем ширину интервала отклонения величины 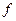от ее среднего значения.

Теперь получим одно полезное выражение для средней квадратичной флуктуации. Для этого в определении этой величины давайте раскроем квадрат разности. В результате получим

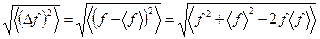. (13)

Далее воспользуемся тем, что среднее суммы равно сумме средних. Таким образом, имеем

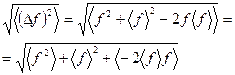. (14)

Теперь воспользуемся тем, что константу можно выносить за знак усреднения. Вынося в третьем слагаемом константу 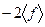, получаем

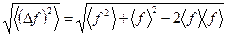. (15)

Сокращая одинаковые слагаемые, окончательно имеем

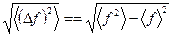. (16)

Таким образом, среднеквадратичная флуктуация определяется разностью среднего квадрата и квадрата среднего.

Отношение 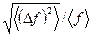называют относительной флуктуацией величины 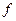. Чем она меньше, тем меньшую часть времени система будет проводить в микросостояниях, в которых отклонение величины 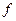от своего среднего значения будет составлять значительную часть последнего.

Покажем теперь, что относительная флуктуация быстро уменьшается с увеличением размеров тела (т.е. с увеличением в нем числа частиц). Для этого предварительно заметим, что большинство величин, представляющих физический интерес являются аддитивными . Это обстоятельство есть следствие того факта, что энергия взаимодействия подсистемы со своим окружением много меньше ее внутренней энергии, и состоит в том, что значение такой величины для всего тела есть сумма значений этой величины для отдельных его макроскопических частей.

Пусть 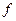есть такая аддитивная величина. Разобьем тело на большое число 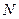примерно одинаковых макроскопических частей. Тогда в силу аддитивности среднее значение нашей величины для всей системы равно сумме средних значений этой величины для частей, на которые мы разбили нашу систему

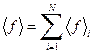. (17)

Если мы теперь будем увеличивать размер тела, сохранив размер частей, т.е. будем “прикреплять” к нашему телу дополнительные части, то у нас будет расти 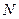. Из (17) ясно, что при увеличении размеров тела среднее 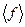системы будет расти примерно пропорционально .

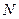Далее определим среднюю квадратичную флуктуацию. Имеем

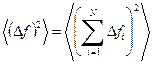. (18)

Отсюда в силу статистической независимости частей

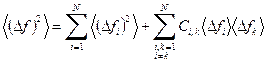. (19)

Поскольку 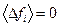для любой подсистемы, то вторая сумма равна нулю, и мы имеем

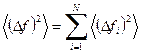. (20)

Из последней формулы видно, что с ростом 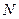среднее квадрата отклонения аддитивной величины, характеризующей все тело, увеличивается приблизительно пропорционально 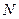, а средне квадратичная флуктуация увеличивается приблизительно пропорционально 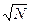. Следовательно, среднеквадратичная флуктуация с ростом 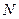будет уменьшаться обратно пропорционально 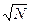, т.е.

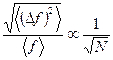. (44)

Когда мы увеличиваем размер тела, сохраняя размер частей, т.е. когда мы добавляем к телу дополнительные части, то число N этих частей, очевидно, будет увеличиваться приблизительно пропорционально числу частиц в теле. Таким образом, можно утверждать, что относительная флуктуация всякой аддитивной величины уменьшается обратно пропорционально квадратному корню из числа частиц в системе. Поскольку в макроскопических телах число частиц колоссально, то относительная флуктуация любой аддитивной величины (а именно такие величины в большинстве случаев представляют физический интерес) будет чрезвычайно мала. Поэтому саму величину можно с большой точностью считать постоянной во времени и равной своему среднему значению.

3. Общие свойства функции распределения. Зависимость функции распределения от макроскопического состояния окружающей среды. Внутренние и внешние термодинамические параметры. Теплообмен.

Функция распределения – это функция 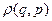, играющая роль плотности вероятности нахождения подсистемы в данной точке ее фазового пространства, зависит от всех координат и импульсов подсистемы.