Монотонно убывающая автокорреляционная функция

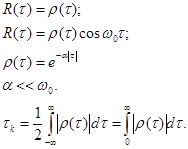
Геометрически время корреляции равно основанию прямоугольника высокой r(0)=1, имеющему ту же площадь, что и площадь заключённую между кривой r(t) и осью абсцисс (t>0, правая полуплоскость).

Величина 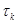даёт представление об интервале времени, когда имеет место коррелированность.

20.Эргодическое свойство стационарных процессов.

До сих пор характеристики случайного процесса были определены через статистические средние значения большого числа реализаций в ансамбле идентичных систем. Оказывается для большинства случайных процессов являющихся стационарными в узком смысле, указанные характеристики можно получить путём усреднения соответствующих величин для одной реализации за достаточно большой промежуток времени. Такая возможность оправдана для однородных во времени процессов, то есть одна реализация достаточно большой продолжительности может содержать все сведения о свойствах случайного процесса. Про такие процессы говорят, что они обладают эргодическим свойством.

Необходимым и достаточным условием эргодичности стационарного процесса является то, что его корреляционная функция в пределе при t®¥ равно 0:

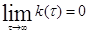-условие эргодичности.

Z (t)-функция стационарного случайного эргодичности процесса x(t).

Z(t) является стационарным и удовлетворяет условиям эргодичности, тогда

<z(t)>= ;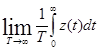

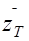-среднее значение одной реализации за Т.

*

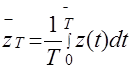Обе части усреднили статистический:

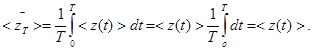
Дисперсия случайной величины 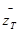стремится к нулю с ростом Т.

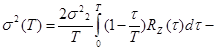показывает что вычисления s(t) необходимо знать корреляционную функцию среднего значения z. Однако есть два частных случая:

1) Т<<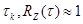

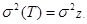
2) Т>> , .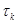

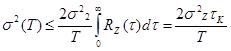Стационарный процесс z(t) удовлетворяет условию 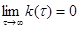. Таким образом с ростом Т случайная величина 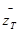стремится к не случайной величине:

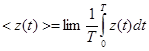-следствие эргодического свойства.

21.Экспериментальное определение математического ожидания, дисперсии и коэффициент корреляции.

Пусть Т – это время эргодического процесса 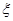(t). Т>> 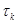, z(t)=x(t).

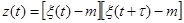, где t - фиксированоÞ

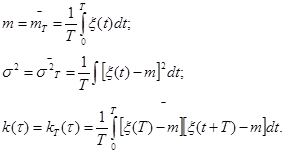
Дисперсия 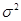равна квадрату эффективного значения переменной постоянного тока или напряжения, определяется прибором с квадратичной характеристикой.

Для определения автокорреляционной функции необходимо специальное счётное устройство, которое называется корелометром или коррелятором.

Основные элементы коррелятора:

1) линия задержки; 2) перемножитель; 3) интегратор и регистрирующий прибор.

Корреляторы бывают дискретные и непрерывные.

Часто интегрирование осуществляется с помощью RC-цепи, а не с помощью идеального интегратора, поэтому могут возникнуть методические ошибки, которые можно вычислить зная аналитическое выражение 4-мерного момента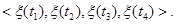

Корреляторы дискретного действия, определение корреляционной функции производится по формуле:

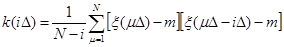, где = .

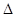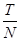Для надёжного определения корреляционной функции число точек должно быть достаточно велико, выбор величины 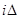производят в зависимости от крутизны функции. Вычисление к(t) производят с малых значений t, про которых функция корреляции мала. Общий вид кривой воспроизводится по точкам.

22.Спектральная плотность. Теорема Хинчина-Винера.

Введём понятие спектральной плотности S(w) стационарного процесса x(t) определив её как преобразование Фурье от автокорреляционной функции:

*

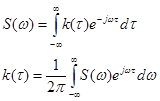при t=0 получили выражение для дисперсии: .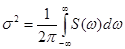

Из условия для корреляционной функции 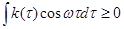следует, что спектральная плотность больше или равна нулю при всех значениях частот.

Если понимать под x(t) флуктуационный ток (напряжение), то величину 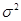можно рассматривать как среднюю мощность на сопротивление 1 Ом. Часть этой мощности S(w)dw/2p относится к составляющим спектром, заключённым между w и w+dw. Поэтому функция S(w) характеризует распределение мощности по спектру. Функцию S(w) называют энергетическим спектром или спектром мощности, т.к. она имеет размерность энергии.

Пара преобразований со * получено одновременно Хинчином и Винером называется формулой Хинчена-Винера. Данная пара обладает теми же свойствами что и преобразование Фурье. В частности, чем шире спектр S(w), тем уже корреляционная функция k(t).

Введём эквивалентную ширину спектра:

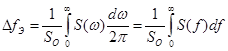, где 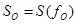, 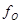- максимальная спектральная плотность.

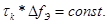
Иногда рассматривают нормализованную спектральную плотность S(w)= 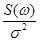. Разделив выражение со * на 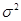, получим:

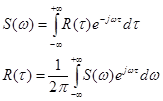
Используя свойство чётности автокорреляционной функции, формулу со * можно записать:

.

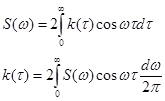Введём понятие физической спектральной плотности для частот f с учётом того, что :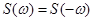

.

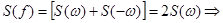
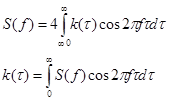В отличие от спектрального детерменисткого анализа спектральная плотность не несёт информации о фазах отдельных спектральных составляющих. Спектральную плотность можно определить следующим образом: рассмотрим ансамбль реализаций стационарной функции с нулевым средним значением Т причём каждая реализация имеет достаточно большую длительность Т. Введём формально спектральную функцию .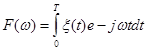

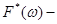комплексно сопряжённая функция с F(w), тогда

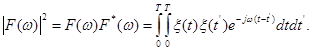
Статистически усредним левую правую часть:

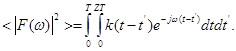
Введя новую переменную t=t- 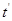после некоторых преобразований получим:

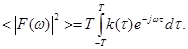
Поделив обе части на Т® 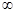и учитывая определение спектральной плотности приходим к формуле:

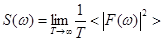-эту формулу можно рассматривать как определение спектральной плотности функции.

23.Экспериментальное определение спектральной плотности.

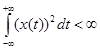-условие сходимости.

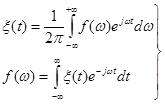
В реальных условиях с точным спектром функции не приходится иметь дело, так как экспериментально не удаётся получить точной гармоники, а можно выделить лишь сумму гармоник лежащих в конечной хотя и малой полосе частот.

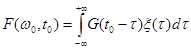(1).

Эта функция представляет собой установившийся случайный процесс на выходе фильтра с импульсной характеристикой G(t).

В дальнейшем предполагаем, что фильтр является узкополосным, 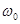-центральная частота.

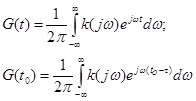
подставим в (1):

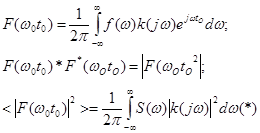
Обозначим максимальное значение модуля передаточной функции фильтра при центральной частоте 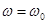через :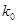

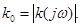
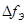-энергетическая полоса пропускания;

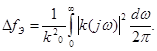
Предположим что модуль передаточной функции настолько узко сконцентрирован вокруг центральной частоты 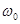, что в пределах полосы частот 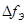спектральную плотность S(w) можно считать постоянной практически:

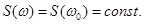
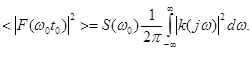
Реальные фильтры имеют действительную импульсную характеристику, поэтому передаточная функция k(jw) отличная от нуля не только при w>0, но и в симметричной области при w<0.

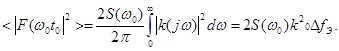
Отсюда для односторонней спектральной плотности получим окончательную формулу:

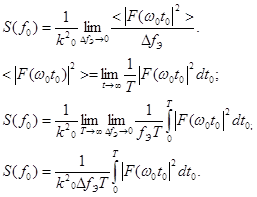
В соответствии с ней для экспериментального определения спектральной плотности стационарного эргодического случайного процесса нужно его пропустить через достаточно узкополосный фильтр, выходной сигнал возвести в квадрат, а потом усреднить за большой интервал времени.

Допустимая величина 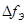определяется характером спектральной плотности, чем она быстрее меняется от частоты, тем меньше необходимо брать 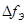. Уменьшение 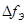увеличивает длительность и время корреляции процесса на выходе фильтра. С уменьшением 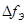нужно увеличивать время интегрировать Т.

24.Функция дискретизации.

Пусть по каналу передаётся f(t). Если передача прерывается с известным ритмом на известное время, то f(t)® 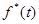, которая представляет собой результат дискретизации f(t).

Дискретизацию можно рассматривать как прерыватель (в пределе).

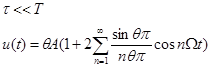
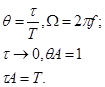
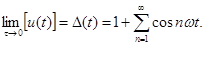
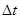-функция дискретизации.

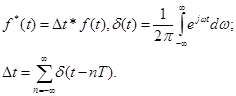
Частотный спектр представляет собой бесконечную последовательность, с линиями дискретизации с частотой w и амплитудой равной .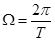

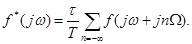
25.Теорема Котельникова во временной области.

Переход решетчатой функции от непрерывной возможен только с ограничениями. Причина ограничений состоит в том, что нужно сохранить возможность восстановления исходной функции f(t), здесь необходимо учитывать ряд факторов:

1) характер изменения сигнала;

2) скорость изменения регистрации сигнал и т.д.

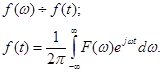
Наложим частотное ограничение. 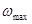-наивысшая частота сигнала f(t).

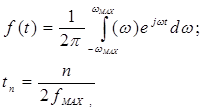
где n-текущее значение отсчётов, 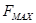- максимальная частота.

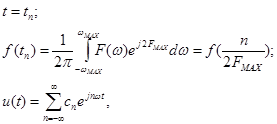
где 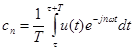коэффициент разложения в ряд Фурье.

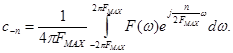
Сравним 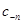и :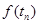

.

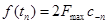Отсюда видно что функция f(t) полностью определяется своим спектром F(w) может быть представлено своим разложением в ряд Фурье, то отсюда следует, что f(t) определяется через свои значения взятые в точках 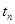с частотой 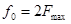. Из сказанного выводится теорема Котельникова:

Если функция f(t) не содержит частот больших 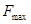, то она полностью определяется дискретным множеством своих значениях взятых с частотой 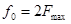, где 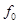-частота дискретизации.

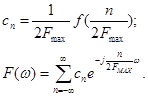
Используем обратное преобразование Фурье:

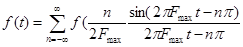-выражение в аналитической форме f(t), то есть ряд Котельникова.

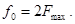
На практике: .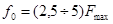

Такой выбор является следствием компромисса между стремлением поднять частоту дискретизации и целью получить сигнал, который может быть более точно воспроизведён в исходном виде и условиями экономии ширины полосы при передаче информации.

26.Теорема Котельникова в частотной области.

f(t) ;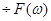

F(w)= ,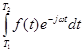

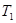и 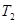-пределы вне которых функция f(t) равна нулю.

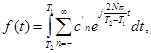где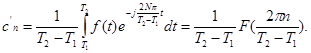

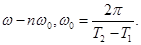
Отсюда мы можем вывести теорему Котельникова:

Если f(t) определена только на интервале 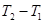, то её спектр F(w) полностью определяется дискретным множеством своих значений, взятых в равноотстоящих точках, разделённых интервалом .

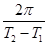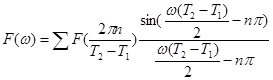-ряд Котельникова в частотной области.