Теорема о разности монотонно убывающей и монотонно возрастающей последовательностях

Теорема о гранях.

Если Х, У не пустые множества вещественных чисел таких, что каждый х?Х, каждый у?У, имеет место х≤у, то существует supХ и infУ, причем такие, что для каждого х и у имеет место: х≤supХ≤infY≤у.

Док-во.

Так как Х ограничено сверху любым у, то существует supХ; У ограничено снизу любым х, то существует infУ: х≤supХ, infY≤у, так как х≤у, то есть каждый у является верхней гранью Х, это наименьшая из верхних граней для каждого у ? У, то есть supХ-нижняя грань У. точная нижняя грань У infХ-это наибольшая из нижних граней, то есть supХ≤infY, тогда: х≤supХ≤infY≤у.

Теоремы о пределе последовательности.

а называется пределом последовательности Xn, если для каждого E>0 найдется такое число, что для всех n>N выполняется |Xn-a|<E, limXn=a (n→∞).

Последовательность, в которой существует предел, называется сходящейся.

Понятие E.

Согласно определению предела, число а является пределом последовательности, если: для каждого n>Ne, |Xn-a|<E, -E<Xn-a<E, a-E<Xn>a+E, данный интервал называется Е окрестности точки а и обозначается Ve(a).

Число а называется пределом последовательности Xn, если для каждой Е окрестности найдется номер, начиная с которого все элементы последовательности принадлежат окрестности.

Теорема.

Если последовательность чисел Хn, a a>p (a<q), то все последовательности будут больше.

Док-во.

LimXn=a, существует Ne такое, что для каждого n>Ne имеет место |Xn-a|<E; a-E<Xn<<a+E; a>p, a-E>p, p<a-E<Xn, a<q, a+E<q, Xn,a+E<q.

Теорема о единственности предела.

Числовая последовательность может иметь только один предел.

Док-во.

Пусть последовательность Xn имеет два предела a и b (a<b).

limXn=a, limXn=b, a<r<b; так как limXn=a, то существует N1, начиная с которого Xn<r, для каждого n>N1: существует N2, Xn> r, для каждого n>N2; N=max(N1,N2); Xn>r и Xn<r, что быть не может.

Теорема об ограниченности последовательности.

Если последовательность имеет предел, то она ограничена.

Док-во.

limXn=a; для каждого n>Ne имеет место |Xn-a|<E; |Xn|=|Xn-a+a|≤|Xn-a|+|a|<E=|a|; E=1, |xn|<1+|a|, для каждого n>Ne=1; max(X1,X2,X3....Xn,1+|a|)=M; Xn≤M для каждого n.

Теорема о трех пределах.

Xn, Yn, Zn; Xn≤Yn≤Zn, для каждого n>N0; limXn=limZn=a, тогда limYn=a.

Док-во.

Так как существуют Xn, Zn, следовательно, Xn?Ve(a), для каждого n>N1, Zn?Ve(a), для каждого n>N2; N=max(N0,N1,N2); для каждого n>N имеет место Xn?Ve(a), Zn?Ve(a), следовательно, limYn=a.

Теорема о сходимости монотонной последовательности.

Если последовательность Xn является возрастающей и ограниченной сверху, то она имеет неограниченный предел limXn=supXn. Если последовательность является убывающей и ограниченной снизу, то существует предел limXn=infXn.

Док-во.

supXn=a; 1. для каждого n?N имеет место Xn≤a; 2. для каждого E>0 существует Ne такое, что Xne>a-E; для каждого n>Ne, a-E<XNe<Xn<a; a-E<Xn<a+E; Xn?Ve(a).

infXn=b; для каждого n?N имеет место Xn>b 2. для каждого E>0 существует Ne такое, что Xne<b+E; для каждого n>Ne, b-E<b≤Xn<Xne<b+E; b-E<Xn<b+E; -E<Xn-b<E; |Xn-b|<E, значит, что предел Хn=b.

Число е.

Рассмотрим последовательность {x_n} = 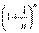. Если последовательность {x_n} монотонная и ограниченная, то она имеет конечный предел. По формуле бинома Ньютона: 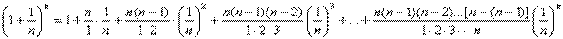или, что то же самое 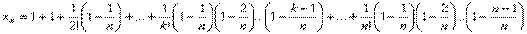. Покажем, что последовательность {x_n} – возрастающая. Действительно, запишем выражение x_n+1 и сравним его с выражением x_n: 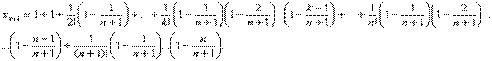_. Каждое слагаемое в выражении x_n+1 больше соответствующего значения x_n, и, кроме того, у x_n+1 добавляется еще одно положительное слагаемое. Таким образом, последовательность {x_n} возрастающая. Докажем теперь, что при любом n ее члены не превосходят трех: x_n < 3.

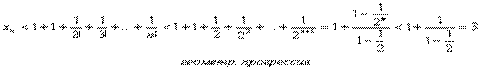.Итак, последовательность 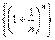- монотонно возрастающая и ограниченная сверху, т.е. имеет конечный предел. Этот предел принято обозначать буквой е.

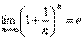.Из неравенства 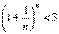следует, что е £ 3. Отбрасывая в равенстве для {x_n} все члены, начиная с четвертого, имеем: 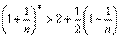переходя к пределу, получаем 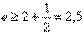. Таким образом, число е заключено между числами 2,5 и 3. Если взять большее количество членов ряда, то можно получить более точную оценку значения числа е.Можно показать, что число е иррациональное и его значение равно 2,71828…

Теорема о разности монотонно убывающей и монотонно возрастающей последовательностях.

Пусть дана монотонно возрастающая последовательность Xn и монотонно убывающая последовательность Yn. Xn<Yn для каждого n. Если их разность стремится к нулю, то они имеют общий конечный предел. Yn-Xn→0, limXn=limYn=c.

Док-во.

Для каждого n, Yn<Y1; Xn<Yn для каждого n; Xn<Y1-ограниченно сверху, следовательно, имеет предел (limXnc); Yn>Xn>X1-ограниченно снизу, следовательно, имеет предел (limYn=c’), по условию теоремы limXn=limYn, следовательно, lim(Yn-Xn)=c’-c=0.