Газов в потоке

Смешение в потоке имеет место в случае объединения потоков различных веществ с различными параметрами в общий поток. Уравнение смешения двух потоков различных газов (жидкостей) при отсутствии их теплообмена с окружающей средой [1,2] имеет вид:

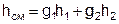, (1)

где h_см, h₁, h₂ – удельные энтальпии смеси газов и ее компонентов,

g₁, g₂ – массовые доли компонентов смеси.

При смешении потоков одного и того же газа с различными температурами, подчиняющегося уравнению состояния идеального газа Рv=RT, температура смеси может быть определена по формуле

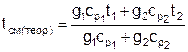, (2)

где g₁, g₂ – массовые доли смешивающихся потоков газа, представляют собой отношение расходов смешивающихся потоков к суммарному расходу смеси

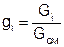, (3)

с_р1, с_р2 – массовые изобарные теплоемкости холодного и нагретого воздуха, определяются по уравнению изобарных теплоемкостей идеальных газов как постоянные величины (в работе воздух рассматривается как двухатомный идеальный газ с m=28,96 кг/кмоль).

Смешение является типичным необратимым процессом и, как всякий необратимый процесс, сопровождается увеличением энтропии системы.

В экспериментальной установке смешиваются два потока воздуха при неизменном атмосферном давлении (рис.1). При таком смешении, если не учитывать теплообмена с окружающей средой, возрастание энтропии системы Ds_см обусловлено необратимым теплообменом между нагретым и холодным воздухом.

Величину Ds_см можно рассчитать по формуле:

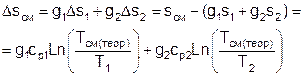, (4)

где s₁, s₂, s_см – энтропии потоков воздуха до смешения и после;

Ds₁, Ds₂ – изменение энтропии каждого из смешивающихся потоков в изобарном процессе смешения.

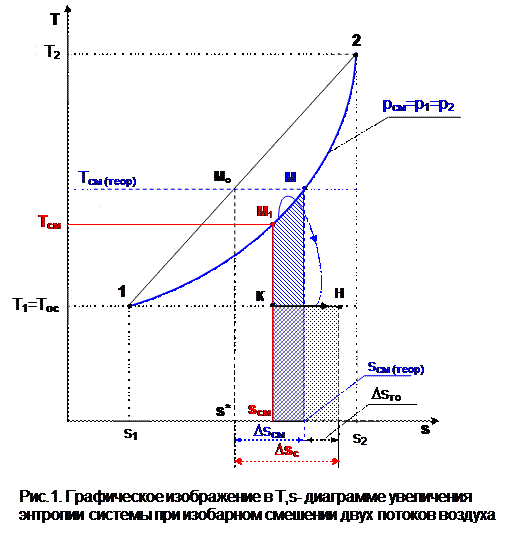
Графически Ds_см – возрастание энтропии системы на 1 кг смеси в диаграмме T,s выражается отрезком М-М_о (рис.1). Здесь кривая 12 соответствует изобаре смешивающихся потоков (все потоки имеют одинаковые давления как и в нашем опыте). Точка М_о, находящаяся на пересечении прямой 12 с изотермой T_{см(теор)}, имеет значение энтропии, соответствующее величине s*=g₁s₁+g₂s₂. Поскольку отрезки прямых Т₂-Т₁ и s₂-s₁ на осях координат по законам геометрии делятся координатами точки М_о в одинаковой пропорции. Пропорциональность этого деления определяется соотношением массовых долей потоков в соответствии с уравнением (2). Так как изобарные теплоемкости всех потоков одинаковы, получим расчетное выражение для температуры смеси в виде

.

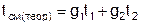При наличии теплообмена с окружающей средой смесь охлаждается от T_{см(теор)} до T_см (процесс М-М₁), отдавая теплоту окружающей среде с температурой Т_ос=Т₁ (процесс К-Н) рис.1. Конечное состояние смеси соответствует точке М₁ .

Увеличение энтропии системы за счет необратимости процесса теплообмена газа с окружающей средой Ds_то определяется как сумма изменений энтропий газа Ds_г и окружающей среды Ds_ос

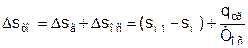, (5)

где 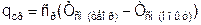– теплота, которую получает окружающая среда при Т_ос=const (площадь под изотермой окружающей среды К-Н) от 1 кг смеси газов (площадь под изобарой М - М₁).

Расчетное выражение (5) увеличения энтропии системы за счет необратимости теплообмена газа с окружающей средой будет иметь вид

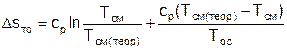, (6)

Полное возрастание энтропии системы Ds_с в расчете на 1 кг смеси определяется как сумма возрастания энтропии за счет процесса смешения Ds_см и необратимого теплообмена Ds_то

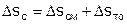. (7)

В диаграмме T,s (рис.1) полному увеличению энтропии системы соответствует сумма отрезков М_оМ и МН по оси абсцисс.