Теоретическое обоснование
ЛАБОРАТОРНАЯ РАБОТА № 11
ИЗУЧЕНИЕ ДИФРАКЦИИ ФРАУНГОФЕРА ПРИ ПОМОЩИ ГАЗОВОГО ЛАЗЕРА
Цель работы: a) наблюдение дифракции на различных объектах;
б) исследование дифракции на одномерной и двумерной решетках.
Приборы и принадлежности: газовый лазер, набор дифракционных объектов, экран, фотоэлемент, микроамперметр.
ТЕОРЕТИЧЕСКОЕ ОБОСНОВАНИЕ
К волновым свойствам света относится и явление дифракции. Дифракционная картина есть результат интерференционного перераспределения энергии по различным направлениям, наблюдаемое в виде чередующихся максимумов и минимумов освещенности.
Дифракционная картина, полученная с помощью круглых отверстий, обладает центральной симметрией и имеет вид чередующихся светлых и темных колец.  Дифракционная картина, полученная с помощью щели, представляет собой чередующиеся максимумы и минимумы. Условия максимумов дифракции от щели удовлетворяют условию
Дифракционная картина, полученная с помощью щели, представляет собой чередующиеся максимумы и минимумы. Условия максимумов дифракции от щели удовлетворяют условию
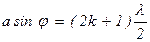 (11.1)
(11.1)
где a – ширина щели, 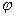 – угол дифракции, к = 1,2, 3… .
– угол дифракции, к = 1,2, 3… .
Дифракционная решетка, представляющая собой совокупность щелей, дает более сложную картину. Она является результатом дифракции от одной и интерференции от многих щелей. Дифракционная картина имеет N–2 дополнительных максимумов и N–1 минимумов, расположенных между главными максимумами. Условие главного максимума имеет вид
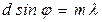 , (11.2)
, (11.2)
где d – постоянная решетки, 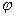 – угол дифракции,
– угол дифракции, 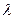 – длина волны,
– длина волны,
m = 0,1,2,3… .
Интенсивность главных максимумов ослабевает по мере увеличения угла дифракции (рис. 11.1).


Рис. 11.1.
Если две одномерные решетки наложить друг на друга так, чтобы щели были взаимно перпендикулярны, то образуется двумерная решетка. Применяя теорию одномерной решетки, можно записать условия главных максимумов для взаимно перпендикулярных направлений:
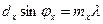 и
и 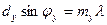 ,
,
где 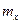 и
и 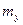 – порядки дифракционных максимумов; dx и dy – периоды решеток;
– порядки дифракционных максимумов; dx и dy – периоды решеток; 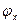 и
и 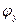 – соответствующие углы дифракции.
– соответствующие углы дифракции.
