Свободные затухающие колебания
Реально любое свободное колебание системы является затухающим. Пусть на колеблющееся тело действует сила сопротивления среды, пропорциональна скорости движения тела
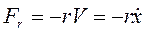 ,
,
где r-коэффициент сопротивления среды.
Тогда второй закон Ньютона можно записать как
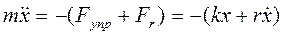
Разделим обе части равенства на m и обозначим 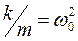 ,
, 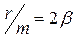 . Тогда дифференциальное уравнение свободных затухающих колебаний будет иметь вид:
. Тогда дифференциальное уравнение свободных затухающих колебаний будет иметь вид:
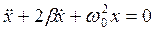 , (1.14)
, (1.14)
где х - колеблющаяся величина; β - коэффициент затухания; ω0 - собственная циклическая частота колебаний. Решение уравнения (1.14) будем искать в виде:
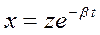 (1.15)
(1.15)
Найдя 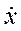 и
и 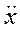 , подставим в (1.8) и получим:
, подставим в (1.8) и получим:
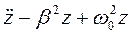 или
или 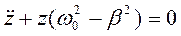
Обозначая 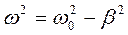 , получим:
, получим: 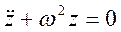 - уравнение гармонических колебаний типа (1.6)
- уравнение гармонических колебаний типа (1.6)
Решением его будет:
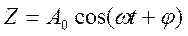 (1.16)
(1.16)
Период
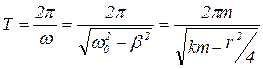
Подставляя (1.16) в уравнение (1.15), получим решение уравнения (1.14):
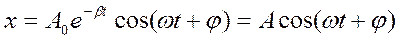 , (1.17)
, (1.17)
где
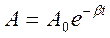
- закон изменения амплитуды со временем t для затухающих свободных колебаний. Скорость затухания определяется коэффициентом затухания:
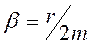
Отношение двух амплитуд, отличающихся по времени на величину Т, называется декрементом затухания:
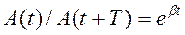
Часто используется логарифмический декремент затухания Q
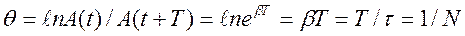 ,
,
где τ - время релаксации (время, в течение которого амплитуда колебаний уменьшается в е раз), N - число колебаний за время τ.
Логарифмический декремент Q величина постоянная для данной системы. Радиотехнические системы характеризуются также добротностью:
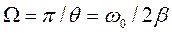
При затухающих колебаниях энергия системы расходуется на преодоление сопротивления среды. Если восполнять эту убыль энергии, то колебания станут незатухающими. Пополнение энергии может осуществляться за счет периодических толчков извне в такт с собственной частотой системы, тогда достигается механический резонанс. Особый технический интерес представляют устройства, имеющие возможность самой колеблющейся системе управлять этим процессом (анкерный механизм часов, генератор и др.). Такие системы называются автоколебательными.
