Движение заряженной частицы в однородном магнитном поле

Как известно, на частицу, движущуюся в магнитном поле действует сила Лоренца 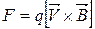Поэтому заряженная частица, влетающая в магнитное поле, отклоняется от своего первоначального направления движения (изменяет траекторию), если только это направление не совпадает с направлением поля. В последнем случае магнитное поле вообще не действует на движущуюся частицу.

Рассмотрим случай, когда частица влетает в однородное поле, созданное в вакууме, имея направление, перпендикулярное полю.

Пусть частица влетает в магнитное поле с индукцией B (рисунок 1). Линии магнитной индукции, изображенные точками, направлены перпендикулярно плоскости рисунка.

Так как скорость перпендикулярна силе Лоренца, то изменяется только направление скорость движения частицы, при этом значение модуля скорости не меняется. Отсюда следует, что траектория частицы является окружностью, на которой частицу удерживает лоренцова сила, играющая роль центростремительной силы. Радиус окружности определим, приравнивая лоренцову и центростремительную силы:

qυB=mυ²/r, (1)

откуда

r=mυ/qB. (2)

Таким образом, радиус окружности, по которой движется частица, пропорционален скорости частицы и обратно пропорционален магнитной индукции поля.

Период обращения частицы равен отношению длины окружности к скорости частицы:

T=2πr/υ. (3)

Откуда

T=2πm/qB. (4)

Следовательно, период вращения частицы в магнитном поле не зависит от ее скорости.

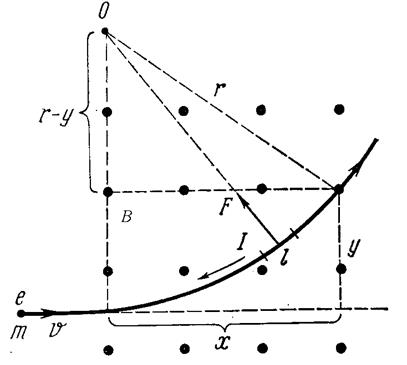Рисунок 1. Движение заряженной частицы в магнитном поле

Если заряженная частица влетает в магнитное поле под углом α, то дальнейшее движение частицы представит собой геометрическую сумму двух одновременных движений: вращения по окружности со скоростью υsinα в плоскости, перпендикулярной линиям напряженности, и перемещения вдоль поля со скоростью υcosα (рисунок 2).

Очевидно, что результирующая траектория частицы окажется винтовой линией с шагом спирали:

h=T^.υ_z. (5)

C помощью рассмотренных закономерностей движения заряженных частиц в магнитном поле можно экспериментально определить удельный заряд частицы:

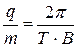(6)

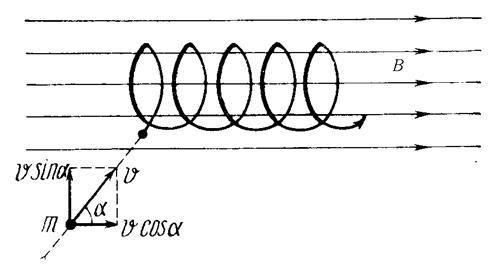Рисунок 2. Движение заряженной частицы под углом к магнитному полю

КОМПЬЮТЕРНЫЙ ЭКСПЕРИМЕНТ

Компьютерный эксперимент дает возможность, изменяя характеристики движения заряда и индукции магнитного поля, определить радиус винтовой или круговой траектории заряда и определять время движения. Измерив период движения заряда, определяют искомый удельный заряд частицы, которая движется, и шаг винта.

ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ

1. Компьютер

2. Программа «Открытая физика 1.1» ООО «Физикон»