Методика изучения кинематических понятий (способы задания

положения точки, перемещение и путь)

Кинематикой начинается изучение раздела «Механика» в курсе физики средней школы, в этой теме изучается основные виды движений тел без учета причин, определяющих характерные особенности этих движений. Кинематика занимает особое место среди других тем школьного курса физики.

Это связано, во-первых, с тем, что в этой теме изучается большинство физических понятий, составляющих основание классической механики как физической теории: материальная точка, абсолютно твердое тело, координата, радиус-вектор, перемещение, скорость, ускорение. С другой стороны эти понятия являются сквозными для всего курса физики – они используются для описания характера движений различных объектов при изучении последующих разделов.

При изучении кинематики конкретизируется и становится понятной суть основной задачи механики: не просто определить положение тела в пространстве в любой момент времени, а, в зависимости от выбранного способа задания положения материальной точки, определить её координату или радиус-вектор в любой момент времени.

Именно в кинематике вводится понятие «система отсчета», что позволяет выяснить абсолютный или относительный характер изучаемых физических величин и начать раскрывать идею относительности, пронизывающую весь курс современной школьной физики.

Все это определяет исключительную важность изучаемых в теме физических явлений и понятий, и необходимость прочного и осознанного их понимания учащимися.

Таким образом, в кинематике изучается механическое движение как физическое явление (и его конкретные проявления) и его основные характеристики.

В самом начале изучения раздела «Механика» вводится понятие механического движения, которое определяется как изменение положения тела или частей тела в пространстве относительно других тел с течением времени и формулируется основная (прямая) задача механики (определить положение тела в любой момент времени). В связи с этим возникает вопрос о необходимости введения физических понятий, характеризующих положение и характер изменения этого положения материальной точки с течением времени. Основными понятиями кинематики в этом случае являются координата, радиус-вектор, путь, перемещение, скорость, ускорение, траектория. В таком случае, описать механическое движение – значит уметь описать характер изменения кинематических величин, то есть уметь записать уравнения движения тела (материальной точки).

В школьном курсе физике рассматривается два способа задания положения точки в пространстве и соответствующие им способы описания механического движения. Первый способ – координатный, при котором положение 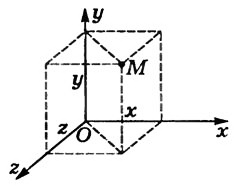материальной точки в пространстве задается посредством координат. В этом случае перемещение вводится как вектор, соединяющий начальное и конечное положения материальной точки, при этом рассматриваются проекции перемещения на координатные оси, величины которых находятся как разность конечной и начальной координаты на соответствующей оси. Зная проекции перемещения на координатные оси, можно определить модуль самого перемещения. Как способ описания движения этот способ называется координатно-векторным.При таком способе описания механического движения кинематические уравнения движения представляют собой зависимость координат от времени х = х (t); у = у (t); z=z(t).

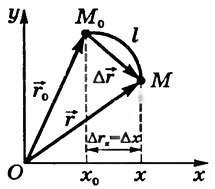Второй способ – векторный, состоит в задании радиус-вектора материальной точки как функции от времени и соответствующее кине матическое уравнение материальной точки имеет вид 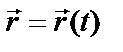. В этом случае перемещение также определяется как вектор, соединяющий начальное и конечное положение точи, но при этом перемещение задается как изменение радиус-вектора материальной точки.

Не смотря на сложность, описание движения с помощью радиус-вектора позволяет раскрыть векторный характер перемещения, скорости и ускорения, к тому же этот способ описания движения более компактен. Векторный характер этих величин был усвоен достаточно хорошо до изучения динамики, где знание векторного характера этих величин необходимо для понимания основных законов движения. Векторная запись уравнений движения в сочетании с соответствующими рисунками (схематическим изображением механических процессов) помогает раскрыть физическую сущность вопросов динамики.

При этом выражения законов механики в векторной форме являются самыми общими и не зависят от выбора системы отсчета. Именно поэтому в старших классах больше внимания необходимо уделять работе с векторными величинами, а вследствие этого выбирается координатно-векторный метод описания движения.

При изучении способов описания механического движения вводится понятие траектории как линии, которую описывает материальная точка при своем движении в пространстве. Это позволяет классифицировать механическое движение по виду траектории - прямолинейное и криволинейное. При этом необходимо рассмотреть различные виды траекторий материальной точки (по окружности, по прямой, по параболе и т.д.), вспомнить из курса математики уравнения соответствующих линий, и на основании этого ввести понятие уравнения траектории материальной точки как функции y(x).

Введение таких кинематических характеристик механического движения как скорость и ускорение делает возможным классифицировать все виды движения по характеру движения (равномерное, неравномерное, равноускоренное).

Рассмотрение видов движения обычно проводится на основе координатно-векторного метода. А для этого необходимо введение понятий «система отсчета», «координаты точки», «перемещение», «траектория». К введению этих понятий учащиеся, в определенной степени, подготовлены на уроках математики. Они умеют определять координаты точки на плоскости и, следовательно, знакомы с понятием системы координат. Отталкиваясь от этих знаний, следует перейти к рассмотрению механического движения материальной точки на плоскости. Анализируя конкретные движения, необходимо раскрыть понятия координаты, вектора перемещения и пути, пройденного телом вдоль траектории.

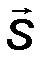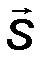l

y1

y2

sy

y

x1

x2

sx

x

Обычно предлагается следующая последовательность рассуждений. Начертив на доске систему координат отмечаем первоначальные координаты мела (х₁, у₁); затем, переместив мел произвольным образом, отмечают другое положение, а следовательно и новые координаты (х₂, у₂). После этого проводим вектор перемещения, отмечаем путь, пройденный точкой вдоль траектории и уточняем, что для определения нового положения тела достаточно указать вектор перемещения. Затем вводится понятие проекций вектора перемещения на координатные оси (на чертеже показываются s_xи s_y) и выясняется, что вектор перемещения однозначно определяется его проекциями.

Доступнее всего для учащихся определение проекции вектора перемещения через разность соответствующих координат s_x= x₂– x_1, s_y= y₂– y₁. При этом важно отметить, что если, например, x₂больше x₁, то проекция вектора перемещения положительна x₂– x₁ >0, если наоборот, то отрицательна.

После этого необходимо записать формулы для нахождения конечных координат точки x₂= x₁ + s_x , y₂= y₁+s_y. Эти формулы будут необходимы при изучении кинематических уравнений конкретных движений.

Практика показывает, что учащиеся нередко путают понятия «путь» и «перемещение», поэтому в методической литературе рекомендуется для конкретизации и разграничения этих понятий предложить учащимся заполнить следующую сравнительную таблицу:

Пройденный путь	Перемещение
1.Путь, пройденный точкой, равен длине отрезка траектории, которая описывается при движении точки из одного положения в другое за данный промежуток времени	1. Направленный отрезок прямой, соединяющий начальное и конечное положение точки при её движении называется перемещением.
2. Пройденный путь — скалярная величина.	2. Перемещение — векторная величина.
3. l = v × t	3.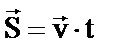
4. Пройденный путь всегда величина положительная	4. Проекция вектора перемещения может быть положительна, отрицательна и равна нулю
5. Между двумя точками путь может быть различным.	5. Перемещение между двумя точками только одно.

Заполнение таблицы должно сопровождаться достаточным числом иллюстраций.

Вопрос о видах движения тесно связан с уравнениями движения. Учащиеся должны уяснить, что уравнения движения в кинематике позволяют решить основную задачу механики: определить положение материальной точки в пространстве в любой момент времени, если известны начальные условия и ускорение.

Впервые школьники обращаются к уравнению движения при рассмотрении простейшей модели - равномерного прямолинейного движения, после введения понятия скорости равномерного прямолинейного движения: 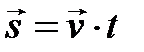- векторная форма или s_x = v_x × t – алгебраическая форма. От уравнения перемещения, записанного через проекции векторов на ось, переходим к уравнению координаты:

х = х₀ + v_x t

Позже, при изучении равноускоренного прямолинейного движения, учащиеся знакомятся с уравнением перемещения для данного типа движения 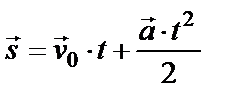и записывают его в проекциях на соответствующие оси

.

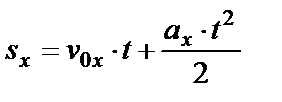Тогда кинематическое уравнение прямолинейного равноускоренного движения будет иметь вид:

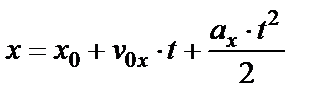
Следует довести до сознания учащихся, что достаточно знать только это уравнение и уравнение скорости, чтобы решить любую кинематическую задачу. Про все остальные уравнения, используемые в кинематике, говорится, что они являются производными от данного основного уравнения, их легко получить из него (желательно показать на примере).

Иногда используется и иной подход к описанию прямолинейного равноускоренного движения (т. е. не вводить понятия проекции вектора перемещения на ось). Для решения уравнений в этом случае вводят «правило знаков»: знак перед ускорением (и скоростью) определяется направлением вектора ускорения (и скорости) относительно выбранной оси (по направлению оси - плюс, против - минус). Однако он легко применим к достаточно простым ситуациям и не обладает такой степенью общности, как первый, заданием проекций.

Изучение кинематики с применением координатно-векторного метода позволяет приблизить трактовку основных понятий и законов механики к той, которая принята в науке, усилить меж­предметные связи физики и математики, осуществить общий под­ход к изучению законов движения и повысить уровень обобщения знаний.

Методика изучения кинематических понятий (скорость, ускорение, уравнения движения)

Способ введения понятий скорости и ускорения зависит от способа введения понятий координат и перемещения материальной точки. При повторении курса основной школы в старших классах необходимо показать, что понятие мгновенной скорости имеет смысл для любого движения, в том числе и равномерного. Этот методический прием исключает возможность образования у школьников неправильного представления о том, что существует несколько понятий скорости.

В старших классах понятие скорости вводят как векторную величину для прямолинейного и криволинейного движений, при этом векторный характер скорости непосредственно вытекает из введения перемещения как векторной величины.

Изучение понятия скорости в несколько этапов.

На первом этапе вводится понятие скорости равномерного движения. При повторении равномерного прямолинейного движения выделить основной его признак: материальная точка в любые равные промежутки времени совершает одинаковые (равные) перемещения. Но равномерные движения разных тел отличаются друг от друга, значит необходимо ввести характеристику движения скорость - величину, которая определяется отношением вектора перемещения ко времени, в течение которого это перемещение произошло. Введение скорости обязательно должно сопровождаться экспериментом.

Далее вводится понятие средней скорости неравномерного движения как скалярной величины. О средней скорости как о векторе можно говорить тогда, когда определяют ее через отношение вектора перемещения к промежутку времени, за который это перемещение совершено. Этот методический подход используют при определении мгновенной скорости.

Учащиеся нередко пытаются определить среднюю скорость как среднеарифметическое начальной и конечной скоростей. Это справедливо только в случае равноускоренного движения. В окружающей нас жизни о средней скорости говорят именно как о величине, равной отношению пути, пройденного телом при движении, к промежутку времени, за который этот путь пройден. Именно это понимание средней скорости и следует выработать у учащихся. Целесообразно решить задачи типа:

1) Первую треть пути тело прошло со скоростью 80 км/ч, остальной путь — со скоростью 20 км/ч. Определите среднюю скорость. 2) Три четверти всего времени движения скорость тела составляла 48 км/ч, остальное время — 96 км/ч. Определите среднюю скорость.

Очень полезно для усвоения понятия скорости и понимания практического выхода этой характеристики ознакомить учащихся с различными значениями скоростей движения тел в окружающей нас жизни, технике, военном деле, используя для этой цели таблицы, предложенные в учебнике. Целесообразна здесь же и работа со справочником. Работая с таблицами, следует добиваться от старшеклассников понимания физического смысла понятия скорости.

Следующим звеном в цепочке формирования основных кинематических характеристик является рассмотрение мгновенной скорости. Трудность введения этого понятия связана с необходимостью введения предельного перехода, еще неизвестного учащимся 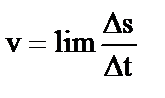при Δt стремящемся к нулю.

По существу, при введении этого понятия в школе используют понятие не математического, а физического предельного перехода: вместо бесконечно малой величины рассматривают очень малый, но конечный промежуток времени - физически малый промежуток времени — такой промежуток, который способен зафиксировать физический прибор.

Понятие мгновенной скорости вводится путем постановки проблемы: с помощью средней скорости нельзя решить основную задачу механики для неравномерного движения.

К примеру можно проанализировать следующую задачу: тело двигалось равномерно в течение промежутка времени t₁ = 20 с со скоростью v₁ = 20 м/с и в течение времени t₂ = 20 с со скоростью v₂ = 30 м/c. Предложить учащимся определить положение тела для любого момента времени.

Для этого им, согласно уже выработанного общего подхода, нужно найти среднюю скорость

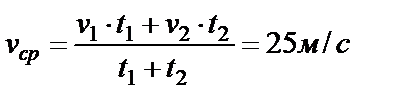
Если теперь определить положение тела к моменту времени t = 10 с, то получим v_ср × t= 250 м, но с другой стороны время t входит в промежуток t₁ = 20 с, где тело двигалось со скоростью v₁ = 20 м/с, Þ S = v₁×t = 200 м.

Это приводит к введению особой характеристики неравномерного движения как скорость в данный момент времени в данной точке траектории, такую скорость и называют мгновенной: мгновенная скорость равна отношению достаточно малого перемещения на участке траектории к промежутку времени, за который это перемещение произошло.

Введение понятия мгновенной скорости обязательно сопровождают экспериментом: это может быть опыт с электронным секундомером и датчиками либо опыт со стробоскопом, где делают стробоскопические снимки одного и того же неравномерного движения с различной частотой вспышек. Аналогично вводят понятие мгновенной скорости и в криволинейном движении.

Методика введения понятия ускорения та же, что и при введении понятия мгновенной скорости. Сначала вводят среднее ускорение за малый промежуток времени, а затем понятие мгновенного ускорения. Однако необходимо предварительно напомнить учащимся о вычитании векторов, чтобы они умели находить век тор изменения скорости.

При введении понятия ускорения выбирают такое неравномерное движение, при котором скорость за любые равные промежутки времени меняется одинаково. Подобно тому, как равномерном прямолинейном движении скорость характеризует быстроту изменения перемещения со временем, так и при равноускоренном прямолинейном движении ускорение характеризует быстроту изменения скорости со временем.

Особое внимание, что знание ускорения позволяет найти мгновенную скорость равноускоренного движения (формула)

Для уяснения понятия ускорения равноускоренного прямолинейного движения целесообразно рассмотреть вопросы типа:

«Ускорение движущегося тела равно 0,2 м/с Что это означает?):

И конечно, полезна работа с таблицей ускорений.

Методика изучения основных понятий динамики (сила и масса)

Понятие массы – одно из наиболее сложных и фундаменталь­ных в науке. Это понятие используют как для объектов макроми­ра (вещественных и полевых), так и для объектов микромира (частиц вещества и частиц поля).

Масса – физическая величина, одна из основных характеристик материи, определяющая инертные и гравитационные свойства. Понятие массы было введено И.Ньютоном в определении импульса тела. Определенная таким образом масса характеризует свойства тела, является мерой его инертности и называется инертной. В теории гравитации Ньютона масса выступает как источник поля тяготения и является мерой гравитационных свойств, поэтому называется гравитационной. В школьном курсе физики изучаются оба типа масс, но понятие инертной массы вводится, а гравитационной нет.

Методика формирования понятия массы при рассмотрении механики в старшей школе базируется на той пропедевтике, которая имела место во вводном курсе 7 класса, а также создает тот фундамент, на котором строится рассмотрение этого понятия во всех последующих разделах систематического курса физики. Можно выделить такие этапы формирования понятия массы.

Исходя из преемственности вводного и систематического курса физики необходимо повторить все основные положения по введению этого понятия во вводном курсе физики.

Затем на основе опытов вводится понятие инертности тел, как свойства тела, заключающееся в том, что для изменения скорости тела необходимо некоторое время и рассматривается способ сравнения инертных свойств двух тел – если при взаимодействии тел у одного из них скорость меняется на меньшую величину, то данное тело более инертно.

Учащиеся уже по опытам, уже зная понятие массы могут заметить, что мерой инертности можно считать именно массу. Таким образом выясняется, что физической величиной, характеризующей инертные свойства тел, является его масса.

Далее проводится опыт на центробежной машине с телами неравной массы, в котором можно измерить ускорение тел и на основании этого сравнить их массы.

m2

m1

n

m₂/m₁ = 2

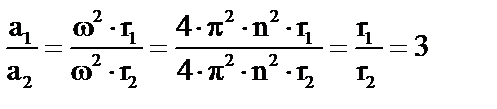
отсюда

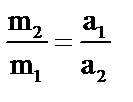
На основании этого опыта учащихся подводят к выводу о том, что для определения массы тела необходимо заставить его провзаимодействовать с неким эталоном, масса которого известна и принята за единицу. При этом раскрывается свойство инертности: нельзя изменить скорость тела мгновенно (для изменения скорости тела необходимо время для различных тел разное, при наличии одинаковых сил — для тел с большей массой — большее, для тел с меньшей массой — меньшее). Дается определение массы: масса тела — физическая величина, характеризующая его инертность. Она определяется отношением ускорения эталона к ускорению тела при их взаимодействии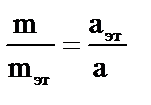

Но так как масса эталона принимается за единицу, то .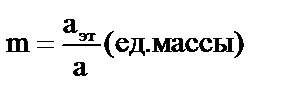

Здесь же необходимо обсудить вопросы об аддитивности массы, единицах измерения массы, двух основных способах измерения массы: на рычажных весах и по взаимодействию тел. Также необходимо рассмотреть вопрос о том, когда нельзя воспользоваться рычажными весами при определении массы (определение массы планет, звезд, микрочастиц), в этом случае применяется второй способ.

Сила в механике рассматривается как мера механического действия на данное материальное тело других тел. Это действие вызывает изменение скоростей точек тела или его деформацию и может иметь место как при непосредственном контакте, так и посредством создаваемых телами полей. Именно эти существенные признаки понятия силы и должны быть сформированы в курсе физики средней школы.

Формирование понятия силы также начинается в 7 классе, где устанавливается, что изменение вектора скорости возможно только при его взаимодействии с другим телом. На основе этого положения и вводится представление о силе (тяжести, упругости, весе, силе трения и силе взаимодействия молекул), затем рассматриваются способ измерения силы и единицы измерения силы.

В 10 классе эти положения повторяются. Определение понятия силы дается как количественная характеристика действия одного тела на другое. Ставятся эксперименты для определения силы, в основе которого лежит положение: сила упругости не зависит от свойств тела, на которое она действует.

Используя это свойство можно действовать на тела различной массы поочередно пружиной с фиксированной длиной, т.е. с силой одинаковой величины.

На известном опыте устанавливается, что для всякого ускоряемого тела при действии одинаковой силы произведение массы тела на его ускорение остается постоянным

m₁×a₁ = m₂×a₂ Þ m×a = сonst

F = m×a

Далее отмечают, что данная формула выражает второй закон Ньютона, после чего дают его словесную формулировку:

Сила, действующая на тело независимо от ее природы, равна произведению массы тела на сообщаемое этой силой ускорение.

Далее вводится понятие о «действии» и «противодействии» в механике при изучении 3 закона Ньютона. Дается следующая формулировка:

Тела действуют друг на друга силами одной и той же природы, равными по модулю и противоположными по направлению — F₁ = - F₂.

При изучении этого закона необходимы экспериментальные доказательства, что действия тел носят взаимный характер. Закон поясняется на основе одного из следующих экспериментов: с двумя динамометрами, эксперимент на закон Архимеда, опыт с подвижными тележками и вентилятором.

Важно очень четко обозначить для учащихся, что в третьем законе рассматриваются в равной степени оба тела, в отличии от второго закона, который относится к одному телу. Термин действие и противодействие – условны и взаимозаменяемы. При взаимодействии двух тел действие 1-го тела на второе можно назвать действием (F12), а 2-го на 1-е противодействием (F21) и наоборот. Важно довести до понимания учащихся, что эти силы приложены к разным телам и что их нельзя складывать, и не следует путать с уравновешенными силами. Уравновешенные силы приложены к одному телу, силы действия и противодействия — к разным, точки их приложения нельзя совмещать.