Многослойные диэлектрические покрытия
Поверхности высокоотражающих лазерных зеркал или делителей пучка обычно изготавливают из многослойных диэлектрических покрытий, нанесенных на оптическую поверхность материала подложки. Применение многослойных диэлектриков для лазерных оптических компонентов связано с тем, что слои делаются из прозрачных материалов и поэтому могут выдерживать высокую интенсивность лазерных пучков.
Рассмотрим оптическую подложку, например стекло, покрытую рядом слоёв с попеременно высоким nH и низким nL показателями преломления по сравнению с показателем преломления nS подложки. (например, TiO2 и SiO2, соответственно). Если толщина слоев 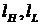 такова, что
такова, что 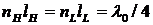 , где λ0 – длина падающей волны в вакууме, то электрические поля от всех отражений на границах слоев будут складываться в фазе. Рассмотрим, например, две границы раздела слоя с высоким показателем преломления (см. рис.). Коэффициент отражения для электрического поля при переходе от среды с низким показателем к высокому
, где λ0 – длина падающей волны в вакууме, то электрические поля от всех отражений на границах слоев будут складываться в фазе. Рассмотрим, например, две границы раздела слоя с высоким показателем преломления (см. рис.). Коэффициент отражения для электрического поля при переходе от среды с низким показателем к высокому
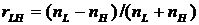
является величиной отрицательной. Это означает, что при отражении электрическое поле претерпевает скачок фазы на π. При переходе от среды с высоким nк среде с низкимn 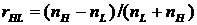 сдвига фазы отраженной волны не происходит. Коэффициент пропускания равен
сдвига фазы отраженной волны не происходит. Коэффициент пропускания равен
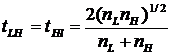 .
.
Если оптическая толщина слоя равна λ0/4, то оба отраженных пучка (см. рис.) сложатся в одной и той же фазе. Этот результат справедлив и для всех многократных отражений (см. случай интерферометра Фабри-Перо).
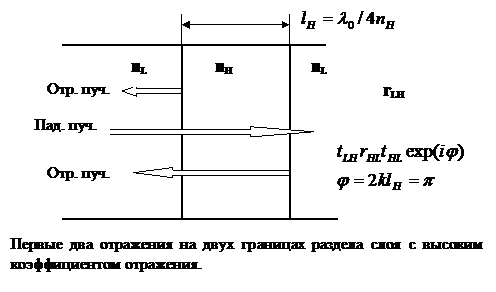
Следовательно, при большом количестве четвертьволновых слоев с попеременным nH nL полная отражательная способность может достигать больших значений. Если многослойное покрытие начинается и заканчивается слоями с высоким показателем преломления, так что число слоев J нечетно, то результирующий коэффициент отражения по мощности запишется в виде:
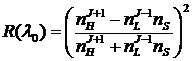
Пример: nS≈1,54 (стекло ВК-7), nH≈2,28 (TiO2, λ≈1 мкм), nL=1,45 (SiO2, λ≈1 мкм), J=15. В этом случае получим R=0,998. Хотя на отдельной границе раздела R=0,049.
Минимальное значение коэффициента отражения достигается, когда 
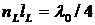 , при этом
, при этом
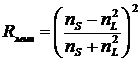
Устойчивость резонаторов
Условие устойчивости сферического резонатора можно получить с помощью геометрической оптики. Рассмотрим луч, выходящий из точки P0, принадлежащей некоторой плоскости β внутри резонатора. После отражения на зеркалах 2 и 1 этот луч пересечет плоскость β в точке P1. Если r0 и r1 – координаты точек P0 и P1 относительно оси резонатора, а r01 и r11 – углы, которые эти лучи образуют с осью резонатора, тогда в соответствии с формулой **) можно написать следующее соотношение:
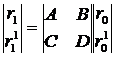 ,
,
где ABCD-матрица – это матрица преобразования лучей, соответствующая полному проходу резонатора. Луч, выходящий из точки P1(r1, r11) после двух отражений, пересечет плоскость β в точке P2(r2, r21), координаты которой определяются выражением
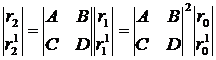
Таким образом, после n полных проходов луча через резонатор координаты точки Pn(rn, rn1) запишутся в виде:
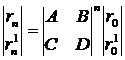
При условии 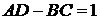 и A+D ≠ 2
и A+D ≠ 2
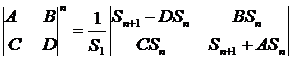 , (3.9)
, (3.9)
где 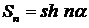 , α определяется соотношением
, α определяется соотношением

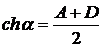 .
.
При этом возможны два случая. Если
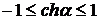 , (3.10)
, (3.10)
то гиперболический косинус переходит в тригонометрический и анализ (3.9) показывает, что в этом случае при прохождении луча через систему он фокусируется. Такая система называется устойчивой. Если условие (3.10) не выполняется, то луч при прохождении системы все более удаляется от оси. Такая система называется неустойчивой.
Чтобы найти условие устойчивости сферического резонатора, мы должны определить соответствующую ему ABCD-матрицу. Если плоскость β расположить непосредственно перед зеркалом 1, то результирующая матрица будет равна произведению следующих четырех матриц. Первая из них описывает распространение луча от зеркала 1 до зеркала 2, вторая – отражение от зеркала 2, третья - распространение луча от зеркала 2 до зеркала 1, четвертая - отражение от зеркала 1.

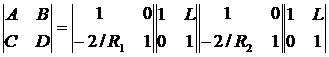
Перемножение матриц дает
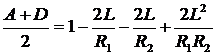 ,
,
Это соотношение преобразуется к виду
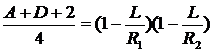
С учетом (3.10), условие устойчивости резонатора запишется так:
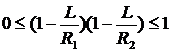 . (3.11)
. (3.11)
Рассмотрим различные виды открытых резонаторов и исследуем их на устойчивость.
1.Если оба зеркала резонатора плоские (R1 =R2= ∞), то система устойчива в точке.
2.Если одно зеркало плоское (R1= ∞ или R2= ∞), а другое сферическое вогнутое, то условие устойчивости будет иметь вид:
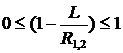 ,
,
т.е. система устойчива в области значений L/R1,2<1. Оптимальный режим соответствует середине области L=R1,2/2.
3.Если оба зеркала сферические вогнутые, то система устойчива, если
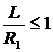 и
и 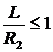 ,
,
т.е. центры обоих зеркал лежат вне резонатора. Система устойчива и при
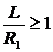
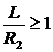 ,
,
т.е. когда центры лежат внутри резонатора, но при выполнении дополнительного условия
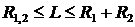 .
.
Система неустойчива, если
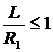 , но
, но 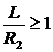 ,
,
или
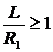 , но
, но 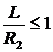
4.Если в резонаторе одно зеркало (R1) вогнутое, а другое (R2) – выпуклое, то условие 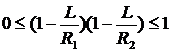 в этом случае будет иметь вид:
в этом случае будет иметь вид:
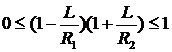 .
.
Для устойчивой работы системы необходимо, чтобы
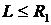 и
и 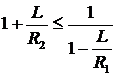 ,
,
или 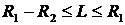 .
.
Рассматриваемая система будет неустойчива, если
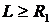 ,
,
а также если 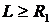 , при условии
, при условии 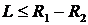 .
.
5. Если оба зеркала выпуклые, то система неустойчива при любых значениях R1, R2 и L.
Условие устойчивости (3.11) удобно представить графически в плоскости g1, g2, где 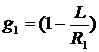 ,
, 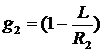 , см. рис.
, см. рис.

На этом рисунке устойчивым резонаторам соответствуют заштрихованные области. Особенно интересный класс сферических резонаторов соответствует точкам прямой линии АС, образующей с осями g1 и g2 угол 450. Эта прямая отвечает симметричным резонаторам (с зеркалами одинаковой кривизны). В частном случае укажем на концентрический (А), конфокальный (В) и плоский (С) резонаторы. Эти резонаторы лежат на границе, разделяющей области устойчивости и неустойчивости. Концентрический резонатор имеет следующие недостатки: 1) очень малый размер пятна в центре резонатора, что может приводить к нежелательным эффектам в лазерах большой мощности, и 2) высокую чувствительность к несоосности зеркал. Поэтому концентрические резонаторы применяются очень редко. В конфокальном резонаторе размер пятна также слишком мал, чтобы можно было эффективно использовать все поперечное сечение лазерной среды. Поэтому конфокальные резонаторы применяются также редко. Высокую эффективность использования поперечного сечения можно получить в плоскопараллельных резонаторах. Однако эти резонаторы также чувствительны к несоосности зеркал. По упомянутым выше причинам, наиболее широко применяемые резонаторы образованы либо двумя вогнутыми зеркалами с большими радиусами кривизны (превышающими длину резонатора в 2-10 раз), либо плоским и вогнутым зеркалом с большим радиусом кривизны. Эти резонаторы дают несколько больший размер пятна, чем конфокальный резонатор, и обладают умеренной устойчивостью к несоосности зеркал. Таким резонаторам на диаграмме соответствует область устойчивости вблизи точки С.
