Тема №2. Электрические цепи однофазного синусоидального тока
2.1. Получение синусоидальной ЭДС, основные соотношения.
Электрические цепи, в которых величины и направления ЭДС, напряжения и тока периодически изменяются во времени по синусоидальному закону, называют цепями синусоидального тока или цепями переменного тока.
В генераторах электростанций возникающая в их обмотках ЭДС изменяется по синусоидальному закону. ЭДС в линейных цепях, где содержатся активные сопротивления, индуктивности и емкости, возбуждает ток, изменяющийся по закону синуса. Возбуждающиеся при этом ЭДС самоиндукции в катушках и напряжения на конденсаторах также изменяются по закону синуса, так как производная синусоидальной функции есть функция синусоидальная
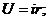
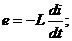
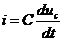 .
.
Любая другая периодическая функция имеет производную, отличную от исходной.
Необходимость использования синусоидального тока обусловлена тем, что коэффициент полезного действия генераторов, двигателей, трансформаторов и линий электропередач получается большим по сравнению с несинусоидальным током. Кроме того, расчет цепей, где ЭДС напряжение и ток изменяются по закону синуса, значительно проще.
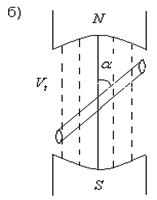
Рассмотрим получение ЭДС и основные соотношения, характерные для синусоидальной ЭДС. Для этого используем модель – проводник, вращающийся в равномерном магнитном поле c угловой скоростью 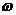 за время
за время 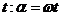 .
.
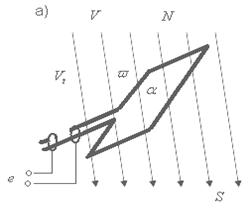
Проводники рамки, перемещаясь в магнитном поле, пересекают его, и в них на основании закона электромагнитной индукции возникает ЭДС (рис.2.1.а). Величина ЭДС пропорциональна магнитной индукции В, длине проводника 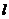 и скорости перемещения проводника относительно поля Vt, или окружной скорости V.
и скорости перемещения проводника относительно поля Vt, или окружной скорости V.

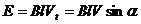 .
.
Наибольшее значение ЭДС в проводнике, возникает при 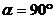
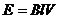 ,
,
мгновенное значение ЭДС, возникающей в проводнике рамки в любой момент времени, равно
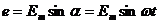 ,
,
где 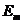 – максимальное или амплитудное значение ЭДС.
– максимальное или амплитудное значение ЭДС.
|
За один оборот рамки происходит полный цикл изменения ЭДС.
Если при t = 0 значение ЭДС не равно нулю, то 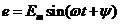 , где
, где 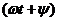
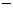 аргумент синуса или фаза, характеризующая значение ЭДС в данный момент времени;
аргумент синуса или фаза, характеризующая значение ЭДС в данный момент времени; 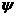
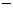 начальная фаза, определяющая значение ЭДС при t=0.
начальная фаза, определяющая значение ЭДС при t=0.
Время, в течение которого совершается один цикл периодического процесса, называется периодом Т, а число периодов в секунду − частотой f, f = 1/T.
Единицей измерения f является 1/c, или Герц (Гц), 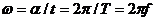 − рад/сек.
− рад/сек.
Выбор частоты промышленных установок в РФ и странах Европы 50Гц обусловлен технико-экономическими соображениями. При меньших частотах габариты, вес и стоимость трансформаторов и машин выше, заметнее пульсации источников света. При увеличении частоты в электрических машинах увеличиваются потери энергии, повышается падение напряжения в проводах.
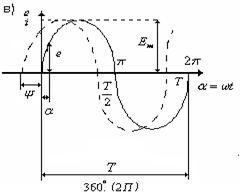
Волновой график зависимости ЭДС от времени изображен на рис.2.1.в) сплошной линией для 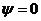 , пунктирной – для
, пунктирной – для 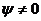 .
.
Синусоидальный ток изменяется во времени по синусоидальному закону: 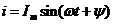 .
.
Т.о., любая синусоидально изменяющаяся функция определяется тремя величинами: амплитудой, угловой скоростью 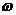 , начальной фазой
, начальной фазой 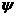 .
.
2.2. Представление синусоидальной функции в комплексной форме.
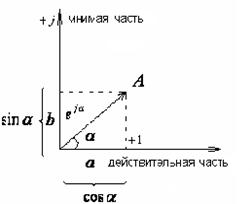
На рис. 2.2. дана комплексная плоскость, на которой можно изобразить комплексные числа.
Комплексное число А имеет действительную (вещественную) часть, которую откладывают по оси абсцисс комплексной плоскости, и мнимую, которую откладывают по оси ординат.
|
Рис.2.2.
На оси действительных значений ставим +1, а на оси мнимых значений +j (j = 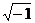 ). Геометрическое изображение числа А – (а+jb).
). Геометрическое изображение числа А – (а+jb).
| |
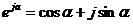 .
. Комплексное число  изображают на комплексной плоскости вектором 0А, численно равным 1 и составляющим угол
изображают на комплексной плоскости вектором 0А, численно равным 1 и составляющим угол 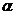 с осью вещественных значений (осью +1). Угол
с осью вещественных значений (осью +1). Угол 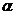 отсчитывают против часовой стрелки от оси +1. Модуль функции находим, используя теорему Пифагора
отсчитывают против часовой стрелки от оси +1. Модуль функции находим, используя теорему Пифагора 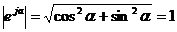 .
.
Проекция множителя вращения вектора  на оси +1 равна
на оси +1 равна 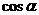 , а на оси +j равна
, а на оси +j равна 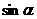 . Умножив обе части формулы Эйлера на амплитудное значение тока
. Умножив обе части формулы Эйлера на амплитудное значение тока 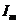 , получим
, получим 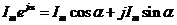 .
.
2.3. Векторные диаграммы.
В электротехнике векторами изображаются ЭДС, напряжения и токи, изменяющиеся по закону синуса.
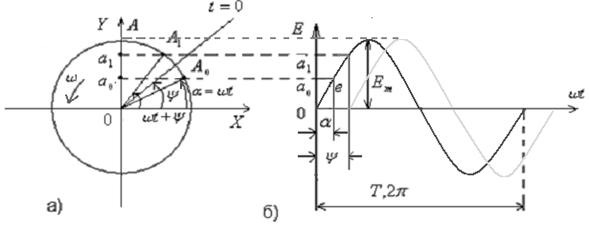
Рис.2.3.
Радиус - вектор 0А (рис.2.3.а) представляющий собой амплитудное значение Еm, вращается с постоянной угловой скоростью 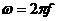 против часовой стрелки. Проекция вектора 0А на вертикальную ось Y равна
против часовой стрелки. Проекция вектора 0А на вертикальную ось Y равна 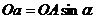 .
.
Выразив 0А через амплитудное значение ЭДС Em и 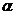 через
через 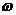 t, получим выражение мгновенного значения ЭДС, изменяющейся по закону синуса
t, получим выражение мгновенного значения ЭДС, изменяющейся по закону синуса
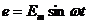
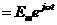 ,
,
комплекс тока при 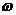 t = 0 запишется как I = Im sin
t = 0 запишется как I = Im sin 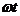 = Im
= Im 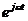
На графике мгновенных значений ЭДС (рис.2.3.б) за начало отсчета выбран момент времени, когда радиус-вектор совпадает с горизонтальной осью Х.
Если в момент t = 0 радиус вектор ОА на рис.2.3.а) расположен под углом 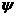 к оси Х
к оси Х 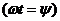 , то проекция Оа’ и, следовательно, e равны
, то проекция Оа’ и, следовательно, e равны
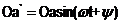 ,
, 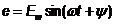 .
.
Аналогичным образом можно представить в виде вектора, вращающегося против часовой стрелки с постоянной угловой скоростью. Мгновенные значения тока и напряжения 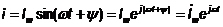 ,
, 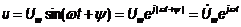
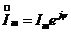 , где I m, Um – комплекс амплитуды.
, где I m, Um – комплекс амплитуды.
Если сложить два тока i1 и i2 с одинаковой частотой, сумма их даст вектор тока с такой же частотой 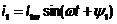 ;
; 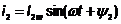 ;
; 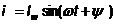 .
.
Для нахождения амплитуды Im и начальной фазы 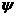 тока на комплексной плоскости (рис. 2.4.а) ток
тока на комплексной плоскости (рис. 2.4.а) ток 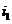 обозначим вектором
обозначим вектором 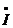 1m= I1m
1m= I1m 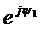 , а ток
, а ток 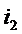
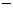 вектором
вектором 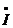 2m= I2m
2m= I2m 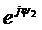 .
.
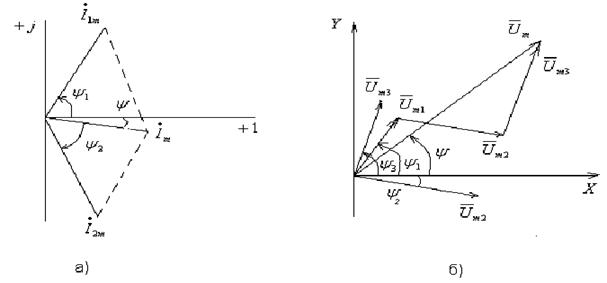
Рис. 2.4.
Геометрическая сумма векторов 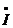 1m и
1m и 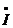 2m дает комплексную амплитуду суммарного тока
2m дает комплексную амплитуду суммарного тока 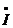 m= Im.
m= Im.
Амплитуда тока 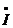 m определяется длинной суммарного вектора, а начальная фаза
m определяется длинной суммарного вектора, а начальная фаза 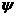
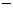 углом, образованным этим вектором и осью +1. При построении векторных диаграмм исходный вектор (рис.2.4.б) располагают на плоскости произвольно (под углом
углом, образованным этим вектором и осью +1. При построении векторных диаграмм исходный вектор (рис.2.4.б) располагают на плоскости произвольно (под углом 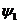 ), остальные векторы
), остальные векторы 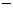 под соответствующими углами (
под соответствующими углами ( 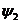 и
и 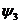 ). Величина и направление векторов сохраняются при последующем построении до получения суммарного вектора
). Величина и направление векторов сохраняются при последующем построении до получения суммарного вектора 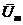 под углом
под углом 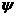 .
.
Если бы векторы I1m, I2m, Im, изображенные на рис. 2.4. стали вращаться вокруг начала координат с одинаковой угловой скоростью 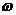 , то взаимное расположение векторов по отношению друг с другом осталось бы без изменений.
, то взаимное расположение векторов по отношению друг с другом осталось бы без изменений.
Обычно векторные диаграммы строят не для амплитудных, а для действующих значений, отличающиеся только масштабами, так как 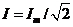 .
.
Итак, векторной диаграммой называют совокупность векторов на комплексной плоскости, изображающих синусоидально изменяющиеся функции времени с одинаковой частотой и построенных с соблюдением правильной ориентации их относительно друг друга по фазе, или более компактное определение 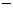 это совокупность нескольких векторов. При построении векторных диаграмм один из нескольких векторов (рис.2.4.б) располагают на плоскости произвольно, остальные векторы под соответствующими углами к исходному.
это совокупность нескольких векторов. При построении векторных диаграмм один из нескольких векторов (рис.2.4.б) располагают на плоскости произвольно, остальные векторы под соответствующими углами к исходному.
2.4. Среднее и действующее значение синусоидально изменяющейся
величины
Под средним значением синусоидально изменяющееся величины понимают среднее арифметическое значение ее за полпериода (т.к. среднее значение за период равно 0). Среднее значение тока может быть найдено из равенства количества тепла Q, выделяющегося за полупериод при переменном и постоянном токе (соответственно, Q1 и Q2). Q1= 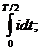 Q2=Iср
Q2=Iср 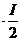 .
.
Приравняв Q1 и Q2, получим 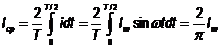 , то есть среднее значение синусоидального тока составляет
, то есть среднее значение синусоидального тока составляет  = 0,637 от амплитудного. Аналогично,
= 0,637 от амплитудного. Аналогично, 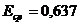 ,
, 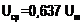 .
.
Количество тепла, выделенное за период синусоидальным током, равно
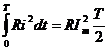 .
.
Количество тепла, выделенное за то же время постоянным током, равно RI2постТ.
Приравняв количество тепла, выделенного переменным и постоянным током за период, получим 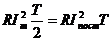 , или
, или 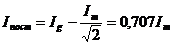 .
.
Т.о., действующее значение синусоидального тока I численно равно значению такого постоянного тока, который за время, равное периоду синусоидального тока, выделяет такое же количество теплоты, что и синусоидальный ток. Когда говорят о величинах напряжения, ЭДС, тока в цепях переменного тока имеют в виду их действующее значение. Действующему значению тока пропорциональна сила, действующая на подвижную рамку измерительного прибора. Шкалы измерительных приборов переменного тока и напряжения градуируются в действующих значениях. Например, если прибор показывает 10 А, то это значит, что амплитуда тока 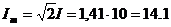 А.
А.
Отношение действующего значения к среднему значению какой-либо периодически изменяющейся величины называется коэффициентом формы кривой. Для синусоидального тока 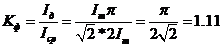 .
.
2.5. Синусоидальный ток в активном сопротивлении.
Сопротивление переменному току, в котором выделяется энергия в виде тепла, называется активным. Сопротивления, в которых энергия запасается в электрическом или магнитном полях, называют реактивными. Реактивными сопротивлениями обладают индуктивности и емкости. Рассмотрим цепь, содержащую только активное сопротивление.
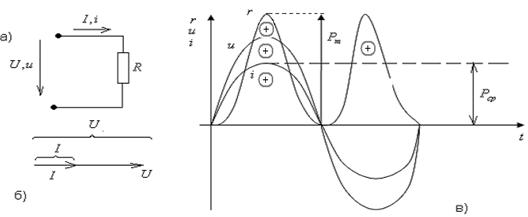 Рис. 2.5.
Рис. 2.5.
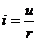 .
.
Выразив мгновенное значение напряжения через амплитудное, получим 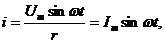 откуда
откуда 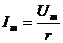 .
.
Разделив левую и правую части на 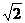 , получим закон Ома для цепи с активным сопротивлением, выраженный действующими значения напряжения и тока
, получим закон Ома для цепи с активным сопротивлением, выраженный действующими значения напряжения и тока 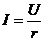 .
.
В активном сопротивлении ток и напряжение совпадают по фазе. Векторная диаграмма цепи изображена на рис. 2.5.б), а осциллограммы, напряжения и мощности 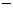 на рис. 2.5.в).
на рис. 2.5.в).
Мгновенная мощность в цепи с активным сопротивлением равна произведению мгновенных значений тока и напряжения
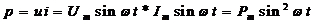 .
.
Мгновенная мощность изменяется от 0 до 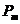 , оставаясь все время положительной. Это означает, что в цепи с активным сопротивлением мощность P все время поступает из сети к потребителю r.
, оставаясь все время положительной. Это означает, что в цепи с активным сопротивлением мощность P все время поступает из сети к потребителю r.
Среднее значение мощности за период
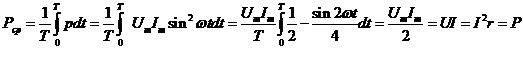
Средняя мощность Рср преобразуется в активном сопротивлении в тепло, называется активной, и измеряется ваттметром в Вт.
2.6. Электрическая цепь с индуктивностью
Обмотки электрических машин, трансформаторов, магнитных усилителей, электромагнитов, реле, контакторов, индукторов электрических нагревательных устройств, печей переменного тока и др. обладают значительной индуктивностью. Параметрами катушек являются активное сопротивление R и индуктивность L. Изменяющийся во времени ток наводит в этих катушках ЭДС самоиндукции, которая затягивает нарастание тока и его спад.
Рассмотрим катушку, в которой сопротивление мало и им можно пренебречь.
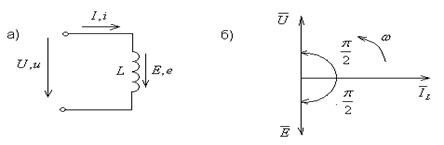
Рис. 2.6.
Если ток в цепи изменяется по синусоидальному закону, то ЭДС самоиндукции
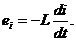
Уравнение, составленное по 2- ому закону Кирхгофа, для цепи? изображенной на рис. 2.6.а), имеет вид
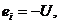 тогда
тогда 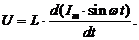
Продифференцировав полученное выражение, получим
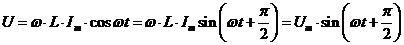 .
.
Таким образом, в цепи с индуктивностью, напряжение на индуктивности изменяется по синусоидальному закону, и опережает по фазе ток на 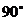 .
.
Напряжение и ток в цепи с индуктивностью связаны соотношениями
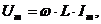
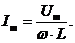
Разделив левую и правую части на 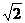 , получим закон Ома для цепи переменного тока с индуктивностью
, получим закон Ома для цепи переменного тока с индуктивностью 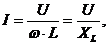 где
где 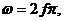
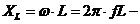 индуктивное сопротивление, Ом.
индуктивное сопротивление, Ом.
Уравнение цепи для действующих значений 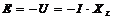 .
.
Т.о., ЭДС самоиндукции может быть определена через ток и индуктивное сопротивление.
Мгновенная мощность в цепи с индуктивностью равна 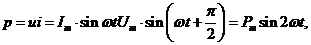
откуда следует, что мгновенная мощность при чисто индуктивной нагрузке изменяется по закону синуса с частотой, в 2 раза большей частоты тока. Амплитудное значение мощности 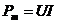 .
.
Осциллограмма рис. 2.7. показывает, что среднее значение мощности за период (активная мощность) равно нулю 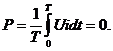
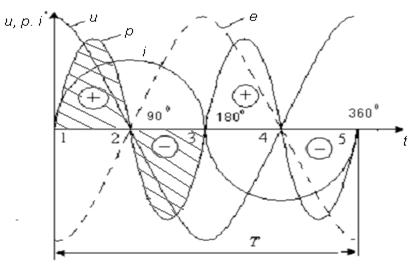
Рис. 2.7.
В интервале от t = 0 (точка 1) до t = 1/4 (точка 2), когда ток в цепи возрастает от 0 до 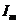 , электрическая энергия из сети поступает в индуктивность, где преобразуется и накапливается в виде магнитного поля. Эта энергия обозначена заштрихованной площадью p и отмечена знаком «+».
, электрическая энергия из сети поступает в индуктивность, где преобразуется и накапливается в виде магнитного поля. Эта энергия обозначена заштрихованной площадью p и отмечена знаком «+».
В интервале времени между точками 2 и 3 ток в цепи убывает. Энергия магнитного поля преобразуется в электрическую и возвращается в сеть. Эта мощность на временном графике р отмечена знаком «-». В точке 3 ток и энергия магнитного поля равна 0.
Из временного графика на рис. 2.7. видно, что площади, определяющие запасенную и отданную энергию, равны. Следовательно, энергия, накопленная в магнитном поле индуктивностью L в первую четверть периода, полностью возвращается в сеть во вторую четверть периода.
В следующую четверть периода в интервале времени между точками 3 и 4 изменяется направление тока и магнитного потока. Происходящий процесс, аналогичен процессу в первой четверти периода.
Т.о., в цепи с индуктивностью происходит непрерывный периодический процесс обмена энергией между источником энергии и индуктивностью, причем потерь энергии при этом не возникает.
2.7. Цепь, содержащая сопротивление- r и индуктивность- L
Катушка любого электротехнического устройства обладает активным сопротивлением R и индуктивностью L. При анализе таких цепей катушку обычно изображают в виде двух идеальных элементов r и L, соединенных последовательно (рис. 2.8.а).
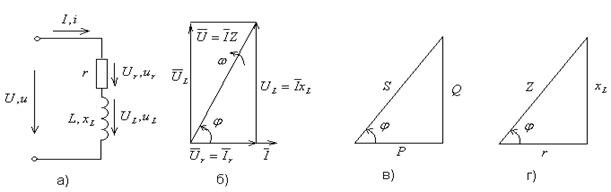
Рис. 2.8.
Уравнение напряжений, составленное по второму закону Кирхгофа для rL-цепи, имеет вид: u = ur + uL ,или в тригонометрической форме: u = Im r 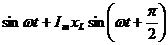 , где ur = Im r
, где ur = Im r 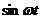
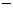 напряжение на активном сопротивлении, совпадающее по фазе с током;
напряжение на активном сопротивлении, совпадающее по фазе с током;
uL = 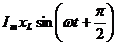
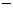 напряжение на индуктивном сопротивлении, опережающее по фазе ток на 90°.
напряжение на индуктивном сопротивлении, опережающее по фазе ток на 90°.
На векторной диаграмме (рис. 2.9.б) вектор 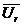 , совпадает с вектором тока, а вектор
, совпадает с вектором тока, а вектор 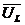 опережает вектор тока на 90°. Из треугольника напряжений следует, что вектор напряжения сети равен геометрической сумме векторов
опережает вектор тока на 90°. Из треугольника напряжений следует, что вектор напряжения сети равен геометрической сумме векторов 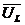 и
и 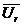 .
. 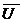 =
= 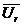 +
+ 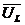 ,
,
а его величина 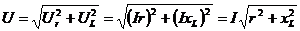 ,
,
откуда 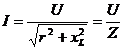 ,
, 
где 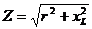
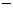 полное сопротивление цепи, Ом.
полное сопротивление цепи, Ом.

а) б)
Рис. 2. 9.
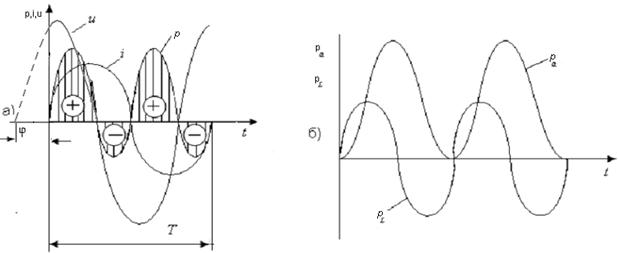
Из векторной диаграммы следует, что напряжение rL- цепи опережает по фазе ток на угол 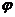 ; мгновенное значение напряжения
; мгновенное значение напряжения 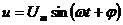 ,
,
угол 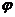 определяют из отношения
определяют из отношения 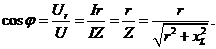
Следовательно, угол 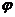 зависит только от параметров цепи r и
зависит только от параметров цепи r и 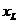 . Умножив стороны треугольника на ток, получим треугольник мощностей (рис.2.9.в), а разделив стороны треугольника напряжений на ток, получим треугольник сопротивления (рис.2.9.г). Стороны треугольника сопротивлений представляют собой отрезки, а не векторы, так как сопротивления есть постоянные, не изменяющиеся по закону синуса величины. Пользуясь треугольником сопротивлений, без расчета и построения векторной диаграммы легко определить
. Умножив стороны треугольника на ток, получим треугольник мощностей (рис.2.9.в), а разделив стороны треугольника напряжений на ток, получим треугольник сопротивления (рис.2.9.г). Стороны треугольника сопротивлений представляют собой отрезки, а не векторы, так как сопротивления есть постоянные, не изменяющиеся по закону синуса величины. Пользуясь треугольником сопротивлений, без расчета и построения векторной диаграммы легко определить 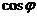 .
.
Мгновенная мощность в r L - цепи с равна произведению мгновенных значений напряжения и тока 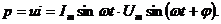
Средняя мощность за период
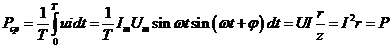 .
.
Выразив произведение синусов через разность косинусов, после интегрирования получим
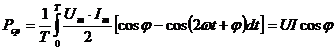 .
.
Полученное выражение показывает, что средняя мощность в rL - цепи есть активная мощность, которая выделяется в активном сопротивлении r в виде тепла. График мгновенных значений напряжения и мощности изображен на рис. 2.9.а). Мгновенную мощность удобно представлять в виде суммы мгновенных значений активной 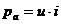 и реактивной (индуктивной)
и реактивной (индуктивной) 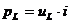 мощностей
мощностей 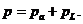
Временные диаграммы 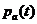 ,
, 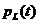 изображены на рис. 2.9.б).
изображены на рис. 2.9.б).
Т.о., энергетические процессы в rL- цепи можно рассматривать как совокупность процессов, происходящих в цепях только с активным сопротивлением r и только с индуктивностью L.
Из временного графика (рис. 2.7.) 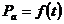 видно, что активная мощность непрерывно поступает из сети, она выделяется в активном сопротивлении в виде тепла
видно, что активная мощность непрерывно поступает из сети, она выделяется в активном сопротивлении в виде тепла 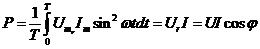 .
.
Мгновенная мощность 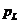 , обусловленная индуктивностью, непрерывно циркулирует между сетью и катушкой. Её среднее значение за период равно нулю.
, обусловленная индуктивностью, непрерывно циркулирует между сетью и катушкой. Её среднее значение за период равно нулю. 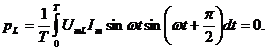
2.8. Цепь, содержащая емкость -С.
В радиоэлектронных устройствах емкость является элементом колебательных контуров, фильтров, элементом связи между контурами и т. д. В силовых установках конденсаторы используют для улучшения коэффициента мощности. В электрических установках емкости образуются между проводами, проводами и землей и другими элементами токоведущих конструкций. При большой протяженности проводов емкость может оказаться значительной и при расчете цепей даже с низкой, например, промышленной частотой, ее необходимо учитывать. В высокочастотных цепях небольшие емкости оказывают существенное влияние на режим работы цепи и их надо учитывать.
Ток в цепи с емкостью С рис. 2.10.а) представляет собой движение зарядов к ее обкладкам 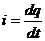 .
.
Выразив заряд q через емкость С и напряжение на емкости 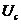 :
: 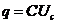 , получим
, получим 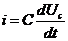 , напряжение на емкости изменяется по закону синуса
, напряжение на емкости изменяется по закону синуса 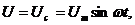 тогда ток в цепи
тогда ток в цепи 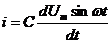 .
.
Взяв производную, получим мгновенное значение тока в цепи с емкостью 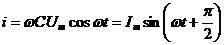 , то есть ток в цепи с емкостью и напряжение на емкости изменяются по закону синуса, но напряжение отстает по фазе от тока на угол 90 о.
, то есть ток в цепи с емкостью и напряжение на емкости изменяются по закону синуса, но напряжение отстает по фазе от тока на угол 90 о.
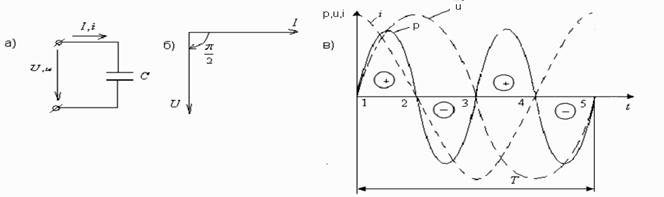
Рис. 2.10.
Векторная диаграмма цепи с емкостью приведена на рис. 2.10.б), а график мгновенных значений тока и напряжения на рис. 2.10.в). Напряжение и ток в цепи с емкостью связаны соотношением
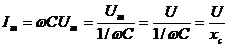 .
.
Напряжение на емкости в цепи переменного тока может быть выражено через произведение тока на емкостное сопротивление 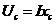 .
.
Мгновенная мощность в цепи с емкостью равна произведению мгновенных значений напряжении и тока
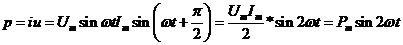 .
.
Из полученного выражения вытекает, что мгновенная мощность изменяется по закону синуса с частотой в два раза большей частоты тока.
Среднее значение мощности за период (активная мощность), равно нулю 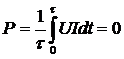 .
.
На временных графиках рис. 2.10.в) в первую четверть периода в интервале между точками 1 и 2, происходит заряд конденсатора: электрическая энергия из сети поступает к конденсатору, преобразуясь и накапливаясь в нем в виде энергии электрического поля. Накопленная энергия равна площади, ограниченной кривой p(t) (отмечена знаком «+») и составляет
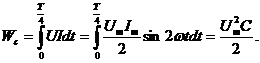
В следующую четверть между точками 2 и 3 происходит разряд конденсатора, энергия электрического поля возвращается в сеть. Энергия, возвращенная в сеть, равна площади ограниченной кривой p(t) (отмеченная знаком «-»).
Из графиков рис. 2.10.в) видно, что площади, определяющие запасенную и отданную энергии, равны. Следовательно, энергия, накопленная в электрическом поле емкости в первую четверть периода, полностью возвращается в сеть во вторую четверть периода.
Таким образом, в цепи с емкостью, также как и в цепи с индуктивностью, происходит непрерывный периодический процесс обмена энергией между сетью и конденсатором, причем потерь энергии при этом не возникает.
2.9. Цепь, содержащая сопротивление- r и емкость-С.
rС-цепь представим как участок, обладающий емкостным сопротивлением 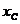 . В этом случае уравнение напряжений цепи имеет вид
. В этом случае уравнение напряжений цепи имеет вид 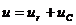 .
. 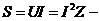 полная (кажущаяся) мощность цепи, ВА,
полная (кажущаяся) мощность цепи, ВА, 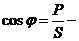 коэффициент мощности цепи.
коэффициент мощности цепи.
Косинус угла сдвига фаз между током и напряжением можно выразить также через сопротивления 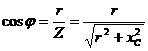 .
.
Мгновенная мощность цепи 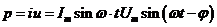 .
.
Средняя мощность за период 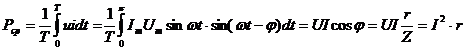 .
.
Мгновенное напряжение на активном сопротивлении совпадает по фазе с током 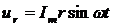
Мгновенное напряжение на емкости отстает по фазе от тока на угол 900
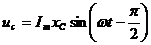 .
.
Мгновенное напряжение, приложенное к цепи
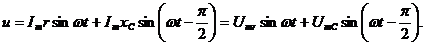
На диаграмме треугольника напряжений вектор 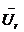 совпадает с вектором тока, вектор
совпадает с вектором тока, вектор  отстает от вектора тока на угол
отстает от вектора тока на угол 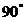 ; вектор напряжения, приложенного к цепи, равен геометрической сумме векторов
; вектор напряжения, приложенного к цепи, равен геометрической сумме векторов 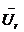 и
и 
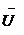 =
= 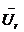 +
+  , а его величина
, а его величина 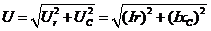 , откуда
, откуда 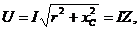 или
или 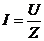 .
.
Полученное выражение представляет закон Ома rС- цепи.
Таким образом, средняя мощность в цепи, содержащей r и С, такая же, как и в r L- цепи и представляет собой активную мощностью, которая выделяется в активном сопротивлении r в виде тепла. Это иллюстрирует график мгновенной мощности цепи с r, С (рис. 2.11.в). Стороны треугольника мощностей (рис. 2. 11.б), представляют
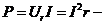 активная мощность цепи, Вт;
активная мощность цепи, Вт;
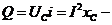 реактивная (емкостная) мощность цепи, ВАр;
реактивная (емкостная) мощность цепи, ВАр;
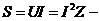 полная (кажущаяся) мощность цепи, ВА;
полная (кажущаяся) мощность цепи, ВА;
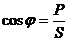 − коэффициент мощности цепи.
− коэффициент мощности цепи.
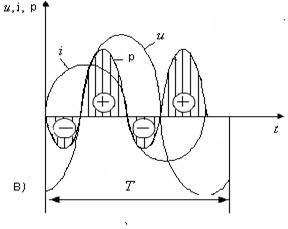
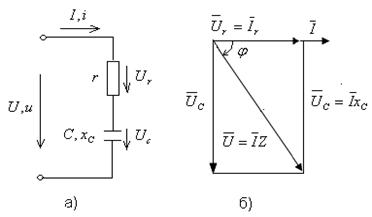
Рис. 2.11.
Измерения активной, реактивной, полной мощностей и 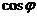 , а также параметров r, С можно произвести с помощью ваттметра, амперметра и вольтметра.
, а также параметров r, С можно произвести с помощью ваттметра, амперметра и вольтметра.
2.10. Построение диаграммы при параллельном соединении потребителей
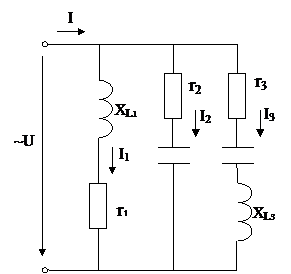
Рассмотрим графоаналитический метод расчета цепи с параллельным соединением потребителей (рис. 2.12.а).
В параллельной цепи напряжения на каждой ветви одинаковы, общий ток равен векторной сумме токов ветвей
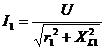 ;
; 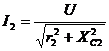 ;
; 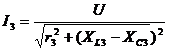 .
.
Угол сдвига φ между током в каждой ветви и напряжением определяются с помощью сos φ
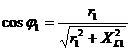 ;
; 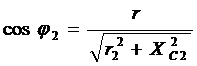 ;
; 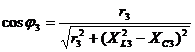 .
.
|
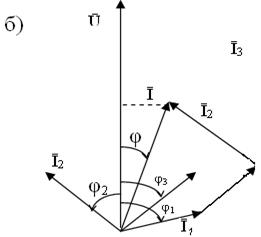
Рис. 2.12.
Общий ток в цепи, как следует из первого закона Кирхгоффа, равен геометрической сумме токов 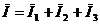 .
.
Значение общего тока определяют графически из векторной диаграммы (рис 2.12.б).
Для анализа разветвленных цепей переменного тока также можно использовать проводимости, с помощью которых разветвлённую цепь можно преобразовать в простейшую цепь и аналитически рассчитать токи и напряжения всех ее участках.
При этом необходимо учитывать, что в цепях переменного тока в отличие от цепей постоянного тока, существует три проводимости – полная, активная и реактивная, причем только полная проводимость является величиной обратной полному сопротивлению последовательного участка цепи.
2.11. Резонанс напряжений
Явления резонанса широко используются в электронных устройствах. Резонанс наступает при равенстве собственной частоты колебаний системы и частоты колебаний возмущающей силы, действующей на систему. Резонанс может возникнуть в цепях переменного тока, где одновременно есть индуктивность и емкость. Собственная частота для идеального контура LC без потерь, когда r = 0
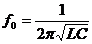 .
.
В общем случае резонансная частота контура 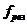 не равна
не равна 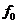 .
.
При резонансе в электрической цепи ток и напряжение совпадают по фазе, и эквивалентная схема представляет собой активное сопротивление (рис.2.13.а). Такое состояние цепи имеет место при равенстве резонансной частоты контура частоте напряжения, подведенного к контуру, малые напряжения, приложенные к цепи, могут вызывать 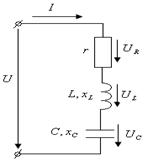 значительные токи и напряжения на отдельных ее участках.
значительные токи и напряжения на отдельных ее участках.
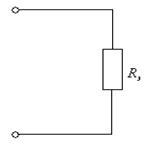

а) б)
Рис. 2.13.
Резонанс напряжений возникает в цепи, где r, L, C соединены последовательно, рассмотрим резонанс напряжений на примере цепи рис. 2.13.б).
Вектор напряжения на активном сопротивлении 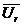 совпадает с вектором тока. Вектор напряжения на индуктивности
совпадает с вектором тока. Вектор напряжения на индуктивности 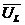 опережает вектор тока на
опережает вектор тока на 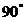 . Поэтому между векторами напряжений на индуктивности и емкости образуется угол
. Поэтому между векторами напряжений на индуктивности и емкости образуется угол 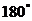 (рис.2.14.а).
(рис.2.14.а).
Если 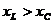 , то и
, то и 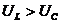 , и векторная диаграмма будет иметь вид, изображенный на рис. 2.14.б).
, и векторная диаграмма будет иметь вид, изображенный на рис. 2.14.б).
Если 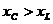 , то векторная диаграмма будет иметь вид, изображенный на рис. 2.14.в).
, то векторная диаграмма будет иметь вид, изображенный на рис. 2.14.в).
При построении диаграмм на рис. 2.14.б) в активное сопротивление катушки неучитывалось, принималось r = 0, 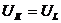 . При резонансе ток контура и напряжение сети совпадают по фазе, угол
. При резонансе ток контура и напряжение сети совпадают по фазе, угол 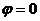 , полное сопротивление цепи равно ее активному сопротивлению r
, полное сопротивление цепи равно ее активному сопротивлению r 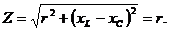
При 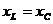 реактивное сопротивление цепи равно нулю, и согласно рис.2.14.а)
реактивное сопротивление цепи равно нулю, и согласно рис.2.14.а) 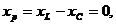 а Z = r.
а Z = r.
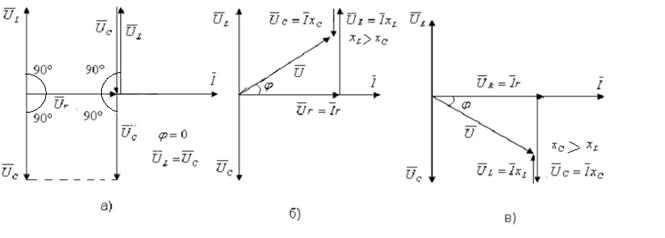
Рис. 2.14.
Выразив 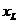 и
и 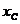 через L, C,
через L, C, 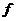 , получим
, получим 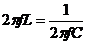 , или
, или 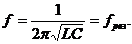
Т.о., частота напряжения, подведенного к контуру, равна резонансной частоте, а 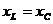 есть условие резонанса напряжений в цепи при последовательном соединении R, L, C.
есть условие резонанса напряжений в цепи при последовательном соединении R, L, C.
Из выражения закона Ома для последовательной цепи вытекает, что ток в цепи при резонансе равен напряжению, деленному на активное сопротивление r = U/r. При резонансе напряжение на индуктивности равно напряжению на емкости 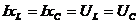 .
.
При больших значениях 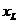 и
и 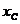 относительно r эти напряжения могут во много раз превышать напряжения сети.
относительно r эти напряжения могут во много раз превышать напряжения сети.
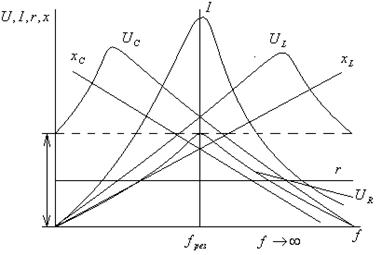 Рис. 2.15.
Рис. 2.15.
При резонансе реактивная энергия циркулирует внутри контура от индуктивности к емкости и обратно, обмена реактивной энергии между источником и цепью не происходит. Ток в проводниках, соединяющих источник с цепью, обусловлен только активной мощностью.
Для анализа цепей часто используют метод частотных характеристик.
На рис. 2.15. изображены графики зависимости Ux, Uс, UL, I, r, Xc, XL от частоты при неизменном напряжении сети.
При f=0: X1 = 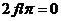 ; Xc=
; Xc= 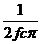 =
= 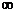 , I=0; Ur=Ir=0; UL=I XL=0; U0= U;
, I=0; Ur=Ir=0; UL=I XL=0; U0= U;
При f = fрез: XL = Xc; I =
