Циркуляция вектора магнитной индукции ,магнитное поле соленоида.

Возьмем контур l (рис. 2.8), охватывающий прямой ток I, и вычислим для него циркуляцию вектора магнитной индукции 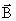, т.е. .

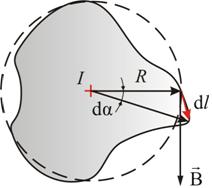
Рис. 2.8

Вначале рассмотрим случай, когда контур лежит в плоскости перпендикулярно потоку (ток I направлен за чертеж). В каждой точке контура вектор направлен по касательной к окружности, проходящей через эту точку (линии прямого тока – окружности).

Воспользуемся свойствами скалярного произведения векторов.

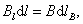где 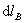– проекция dl на вектор 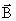, но 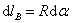, где R – расстояние от прямой тока I до dl.

.

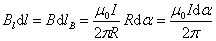Отсюда

,

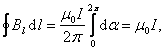(2.6.1)

это теорема о циркуляции вектора 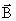: циркуляция вектора магнитной индукции равна току, охваченному контуром, умноженному на магнитную постоянную.

Иначе обстоит дело, если ток не охватывается контуром (рис. 2.9).

При обходе радиальная прямая поворачивается сначала в одном направлении (1–2), а потом в другом (2–1). Поэтому 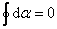, и следовательно

,

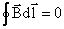(2.6.2)

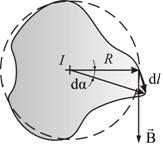
Рис. 2.9

Итак, 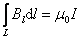, где I – ток, охваченный контуром L.

Эта формула справедлива и для тока произвольной формы, и для контура произвольной формы.

Если контур охватывает несколько токов, то

,

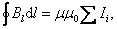(2.6.3)

т.е.циркуляция вектора 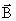равна алгебраической сумме токов, охваченных контуром произвольной формы.

Теорема о циркуляции вектора индукции магнитного поля 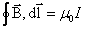позволяет легко рассчитать величину В от бесконечного проводника с током (рис. 2.10): .

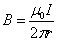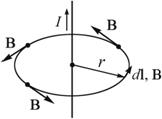
Рис. 2.10

Итак, циркуляция вектора магнитной индукции 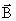отлична от нуля, если контур охватывает ток (сравните с циркуляцией вектора : ).

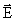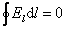Такие поля, называются вихревыми или соленоидальными.

Магнитному полю нельзя приписывать потенциал, как электрическому полю. Этот потенциал не был бы однозначным: после каждого обхода по контуру он получал бы приращение .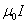

Линии напряженности электрического поля начинаются и заканчиваются на зарядах. А магнитных зарядов в природе нет. Опыт показывает, что линии 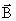всегда замкнуты (см. рис. 1.2. и 1.7). Поэтому теорема Гаусса для вектора магнитной индукции 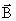записывается так:

.

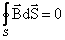Применим теорему о циркуляции вектора 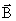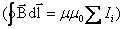для вычисления простейшего магнитного поля – бесконечно длинного соленоида, представляющего собой тонкий провод, намотанный плотно виток к витку на цилиндрический каркас (рис. 2.11).

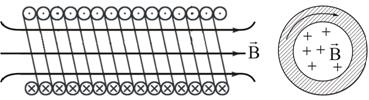
Рис. 2.11

Соленоид можно представить в виде системы одинаковых круговых токов с общей прямой осью.

Бесконечно длинный соленоид симметричен любой, перпендикулярной к его оси плоскости. Взятые попарно (рис. 2.12), симметричные относительно такой плоскости витки создают поле, в котором вектор перпендикулярен плоскости витка, т.е. линии магнитной индукции имеют направление параллельное оси соленоида внутри и вне его.

Рис. 2.12

Из параллельности вектора оси соленоида вытекает, что поле как внутри, так и вне соленоида должно быть однородным.

Возьмём воображаемый прямоугольный контур 1–2–3–4–1 и разместим его в соленоиде, как показано на рисунке 2.13.

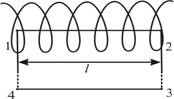
Рис. 2.13

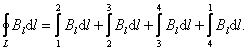
Второй и четвёртый интегралы равны нулю, т.к. вектор перпендикулярен направлению обхода, т.е .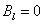

Возьмём участок 3–4 – на большом расстоянии от соленоида, где поле стремится к нулю; и пренебрежём третьим интегралом, тогда

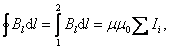
где 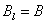– магнитная индукция на участке 1–2 – внутри соленоида, 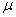– магнитная проницаемость вещества.

Если отрезок 1–2 внутри соленоида, контур охватывает ток:

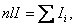
где n – число витков на единицу длины, I – ток в соленоиде (в проводнике).

Тогда магнитная индукция внутри соленоида:

,

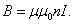(2.7.1)

Вне соленоида:

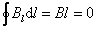и 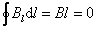, т.е. .

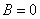Бесконечно длинный соленоид аналогичен плоскому конденсатору – и тут, и там поле однородно и сосредоточено внутри.

Произведение nI – называется число ампер витков на метр.

У конца полубесконечного соленоида, на его оси магнитная индукция равна:

,

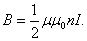(2.7.2)

Практически, если длина соленоида много больше, чем его диаметр, формула (2.7.1) справедлива для точек вблизи середины, формула (2.7.2) для точек около конца.

Если же катушка короткая, что обычно и бывает на практике, то магнитная индукция в любой точке А, лежащей на оси соленоида, направлена вдоль оси (по правилу буравчика) и численно равна алгебраической сумме индукций магнитных полей создаваемых в точке А всеми витками. В этом случае имеем:

· В точке, лежащей на середине оси соленоида магнитное поле будет максимальным:

,

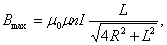(2.7.3)

где L – длина соленоида, R – радиус витков.

· В произвольной точке конечного соленоида (рис. 2.14) магнитную индукцию можно найти по формуле

,

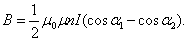(2.7.4)

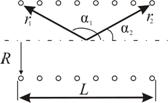
Рис. 2.14

На рисунке 2.15 изображены силовые линии магнитного поля : а) металлического стержня; б) соленоида; в) железные опилки, рассыпанные на листе бумаги, помещенной над магнитом, стремятся вытянуться вдоль силовых линий; г) магнитные полюсы соленоида.

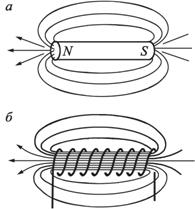
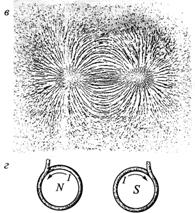
Рис. 2.15