Волны в упругой среде. Поперечные и продольные волны. Уравнение волны и основные характеристики.
Упругими волнами – это процесс распространения колебанийв упругой среде.
Упругие волны бывают продольные и поперечные. В продольных волнах частицы среды колеблются в направлении распространения волны, в поперечных — в плоскостях, перпендикулярных направлению распространения волны.
Продольные волны могут возбуждаться в средах, в которых возникают упругие силы при деформации сжатия и растяжения, т. е. твердых, жидких и газообразных телах. Поперечные волны могут возбуждаться в среде, в которой возникают упругие силы при деформации сдвига, т. е. в твердых телах; в жидкостях и газах возникают только продольные волны, а в твердых телах — как продольные, так и поперечные.
Уравнение волны и основные характеристики
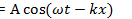 – уравнение волны
– уравнение волны
волна распространяется вдоль ось Ох.
k-волновое число, оно показывает сколько раз укладывается х в нем.
 - длина волны
- длина волны
Длина волны – это минимальное расстояние между точками, которые колеблются в одинаковой фазе.
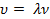
 - скорость распространения волны
- скорость распространения волны
 - частота колебаний
- частота колебаний
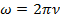
 - циклическая частота
- циклическая частота
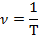
Т – период колебания
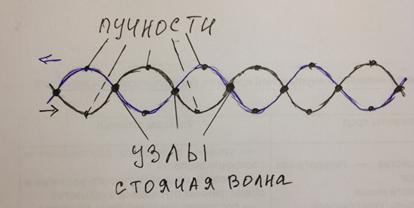
Стоячие волны. Амплитуда стоячей волны. Узлы и пучности. Длина стоячей волны.
Стоячее волны — это волны, образующиеся при наложении двух бегущих волн, распространяющихся навстречу друг другу с одинаковыми частотами и амплитудами, а в случае поперечных волн и одинаковой поляризацией.
Амплитуда стоячей волны:
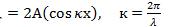 - волновое число.
- волновое число.
Каждая точка совершает гармоническое колебание с периодом Т. Амплитуда Аст для каждой точки вполне определена. Но при переходе от одной точки волны к другой она изменяется в зависимости от расстояния х. Если придавать х значения, равные 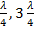 и т.д., то при подстановке в уравнение получим
и т.д., то при подстановке в уравнение получим 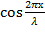 . Следовательно, указанные точки волны остаются в покое, т.к. амплитуды их колебаний равны нулю. Эти точки называются узлами стоячей волны. Точки, в которых колебания происходят с максимальной амплитудой, называются пучностями. Расстояние между соседними узлами (или пучностями) называются длиной стоячей волны и равно
. Следовательно, указанные точки волны остаются в покое, т.к. амплитуды их колебаний равны нулю. Эти точки называются узлами стоячей волны. Точки, в которых колебания происходят с максимальной амплитудой, называются пучностями. Расстояние между соседними узлами (или пучностями) называются длиной стоячей волны и равно
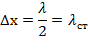
где λ - длина бегущей волны.
Статические и термодинамические методы исследования вещества. Состояние, процесс, термодинамические параметры. Термодинамическое решение. Модель идеального газа. Газовые законы. Основное уравнение молекулярно-кинетической теории.
Законы поведения огромного числа молекул, являясь статистическими закономерностями, изучаются с помощью статистического метода. Этот метод основан на том, что свойства макроскопической системы в конечном счете определяются свойствами частиц системы, особенностями их движения и усредненными значениями динамических характеристик этих частиц. Термодинамика не рассматривает микропроцессы, которые лежат в основе этих превращений. Этим термодинамический метод отличается от статистического. Термодинамика базируется на двух началах — фундаментальных законах, установленных в результате обобщения опытных данных.
Переход из одного термодинамического состояния в другое называется термодинамическим процессом. Равновесным состоянием - состоянием термодинамического равновесия - называется такое состояния термодинамической системы, в котором отсутствуют всякие потоки (энергии, вещества, импульса и т. д.), а макроскопические параметры системы являются установившимися и не изменяются во времени. Если какая-либо термодинамическая система находится в термодинамическом равновесии с двумя другими системами, то и эти две системы находятся в термодинамическом равновесии друг с другом.
Модель идеального газа
- Число молекул в газе велико: N>> 1, среднее расстояние между отдельными молекулами много больше их размеров (l>>a).
- Молекулы газа совершают неупорядоченное, хаотическое движение.
- Движение отдельных молекул подчиняется законам механики, молекулы рассматриваются как материальные точки, совершающие только поступательное движение. Величина потенциальной энергии взаимодействия мала по сравнению со средней кинетической энергией.
- Все соударения молекул друг с другом и со стенками сосуда, в котором находится газ, являются абсолютно упругими При ударе о стенку компонента импульса молекулы, перпендикулярная стенке, меняет знак. Выполняются законы сохранения импульса и энергии для молекул газа.
Произведение давления идеального газа на его объем пропорционально плотности числа молекул в газе и средней кинетической энергии поступательного движения отдельной молекулы,т.е.
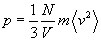
Изотермический процесс. Процесс изменения состояния системы макроскопических тел (термодинамической системы) при постоянной температуре . 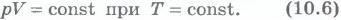
Изобарный процесс. Процесс изменения состояния термодинамической системы при постоянном давлении 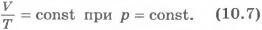
Изохорный процесс. Процесс изменения состояния термодинамической системы при постоянном объеме. 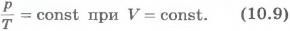
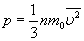 -основное уравнение мкт.
-основное уравнение мкт.
Обозначив среднее значение кинетической энергии поступательного движения молекул идеального газа 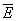 :
: 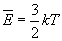 , получим
, получим 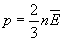 .
.
