Модель идеального газа. Изозаконы.

В МКТ пользуются моделью идеального газа, согласно которой:

1) собственный объём молекул газа пренебрежимо мал по сравнению с объёмом сосуда.

2) между молекулами газа отсутствуют силы взаимодействия.

3) столкновения молекул газа между собой и стенками сосуда абсолютно упругие.

Модель идеального газа можно использовать при изучении реальных газов, т.к. они в условиях, близких к нормальным (кислород, гелий), а также при низких давлениях и высоких температурах близки по своим свойствам к идеальному газу(иг).

Опытным путём, ещё до появления МКТ, был установлен целый ряд законов, описывающих поведение иг’ов:

1) Закон Бойля-Мариотта (изотерма): для данной массы газа при постоянной температуре произведение давления газа на его объём есть величина постоянная:

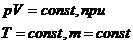
изотерма – кривая (гипербола), изображающая зависимость между величинами P и V , характеризующими св-ва вещ-ва, при постоянной Т.

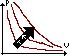
2) Закон Гей-Люссака(изобара):

1. объём данной массы газа при постоянном давлении изменяется линейно с температурой:

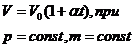
2. (Шарля) давление данной массы газа при постоянном объёме изменяется линейно с температурой.

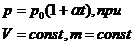
В этих уравнениях t – температура по шкале Цельсия, р₀ и V₀ – давление о объём при 0^оС, коэффициент .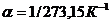

Изобарный – процесс, протекающий при постоянном давлении.

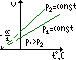
изохорный – процесс, протекающий при постоянном объёме.

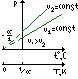
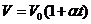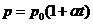Вводя в формулы и термодинамическую температуру, получим:

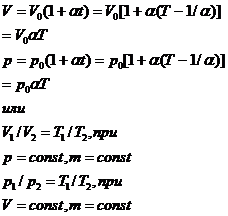
Основное уравнение МКТ.

Для вывода основного уравнения МКТ рассмотрим одноатомный идеальный газ. Предположим, что молекулы газа движутся хаотически, число взаимных столкновений между молекулами газа пренебрежимо мало, по сравнению с числом удара о стенки сосуда.

Выделим на стенке сосуда элементарную площадку 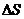, и вычислим давление, оказываемое на эту площадку. При каждом соударении молекула, движущаяся перпендикулярно площадке передаёт ей импульс: 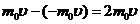. За время 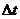площадки достигнут, только те молекулы, которые находятся в объёме цилиндра с основанием 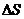и высотой 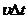. Число этих молекул равно 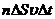(n-концентрация).

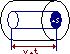
Необходимо учесть, что реально молекулы движутся к площадке под разными углами, и имеют различные скорости, причём скорость молекул при каждом соударении меняется. Для упрощения расчётов хаотическое движение молекул заменяют движением вдоль 3-х взаимно перпендикулярных направлений, так что в любой момент движения вдоль каждого из них движется 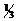молекул, причём половина молекул ( 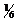) движется вдоль данного направления в одну сторону, половина в другую. Тогда число ударов молекул, движущихся в заданном направлении, о площадку 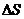будет 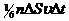. При столкновении с площадкой эти молекулы предадут ей импульс

,

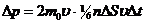
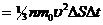тогда давление газа на стенку равно:

Средняя квадратичная скорость:

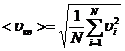
хар-ет всю совокупность молекул газа.

С учётом этой формулы:

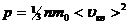
Это и есть основное уравнение МКТ.

Учтя, что 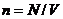получим:

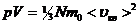,или

,

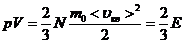где Е – суммарная кинетическая энергия поступательного движения всех молекул.

Т.к. 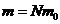, то:

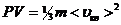
Для одного моля газа m=M ( M – молярная масса):

,

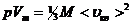где V_m- молярный объём. По уравнению Менделеева – Клапейрона pV_m=RT, т.о.:

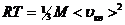, откуда:

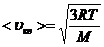
т.к. 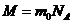, то

,

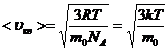где 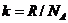- постоянная Больцмана.

Средняя кинетическая энергия поступательного движения одной молекулы иг:

.
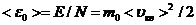
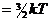