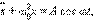Логарифмический декремент затухания

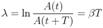
Добро́тность — характеристика колебательной системы, определяющая полосу резонанса и показывающая, во сколько раз запасы энергии в системе больше, чем потери энергии за один период колебаний.

Добротность обратно пропорциональна скорости затухания собственных колебаний в системе. То есть, чем выше добротность колебательной системы, тем меньше потери энергии за каждый период и тем медленнее затухают колебания.

Общая формула для добротности любой колебательной системы:

,

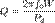где: 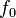— резонансная частота колебаний 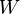— энергия, запасённая в колебательной системе

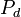— рассеиваемая мощность.

Например, в электрической резонансной цепи энергия рассеивается из-за конечного сопротивления цепи, в кварцевом кристалле затухание колебаний обусловлено внутренним трением в кристалле, в объемных электромагнитных резонаторах теряется в стенках резонатора, в его материале и в элементах связи, в оптических резонаторах — на зеркалах.

Для Колебательного контура в RLC цепях:

,

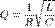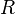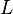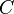где , и — сопротивление, индуктивность и ёмкость резонансной цепи, соответственно.

25. Вынужденные колебания — колебания, происходящие под воздействием внешних сил, меняющихся во времени.

Автоколебания отличаются от вынужденных колебаний тем, что последние вызваны периодическим внешним воздействием и происходят с частотой этого воздействия, в то время как возникновение автоколебаний и их частота определяются внутренними свойствами самой автоколебательной системы.

Наиболее простой и содержательный пример вынужденных колебаний можно получить из рассмотрения гармонического осциллятора и вынуждающей силы, которая изменяется по закону: .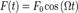

Колебания, совершающиеся под воздействием внешней периодической силы, называются вынужденными. Внешняя сила совершает положительную работу и обеспечивает приток энергии к колебательной системе. Она не дает колебаниям затухать, несмотря на действие сил трения.

Если свободные колебания происходят на частоте ω0, которая определяется параметрами системы, то установившиеся вынужденные колебания всегда происходят на частоте ω внешней силы.

В начальный момент в колебательной системе возбуждаются оба процесса – вынужденные колебания на частоте ω и свободные колебания на собственной частоте ω0.

Но свободные колебания затухают из-за неизбежного наличия сил трения. Поэтому через некоторое время в колебательной системе остаются только стационарные колебания на частоте ω внешней вынуждающей силы. Внешняя

сила 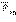приложена к свободному концу пружины. Она заставляет свободный (левый на рис. 2.5.1) конец пружины перемещаться по закону

y = ym cos ωt.

где ym – амплитуда колебаний, ω – круговая частота. Такой закон перемещения можно обеспечить с помощью шатунного механизма, не показанного на рис. 2.5.1.

Уравнению, выражающему второй закон Ньютона для тела на пружине при наличии внешнего периодического воздействия, можно придать строгую математическую форму, если учесть связь между ускорением тела и его

координатой: 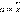Тогда уравнение вынужденных колебаний запишется в виде

(**)

где 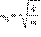– собственная круговая частота свободных колебаний, ω – циклическая частота вынуждающей силы. В случае вынужденных колебаний груза на пружине (рис. 2.5.1) величина A определяется выражением:

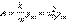Зависимость амплитуды xm вынужденных колебаний от частоты ω вынуждающей силы называется резонансной характеристикой или резонансной кривой

Наиболее известная большинству людей механическая резонансная система — это обычные качели. Если вы будете подталкивать качели в соответствии с их резонансной частотой, размах движения будет увеличиваться, в противном случае движения будут затухать. Резонансную частоту такого маятника с достаточной точностью в диапазоне малых смещений от равновесного состояния, можно найти по формуле: 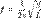,где g это ускорение свободного падения (9,8 м/с² для поверхности Земли), а L — длина от точки подвешивания маятника до центра его масс.

частота главного резонанса зависит от свойств струны и выражается следующим отношением:

,

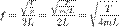где T — сила натяжения, ρ — масса единицы длины струны, а m — полная масса струны.Увеличение натяжения струны и уменьшение её массы (толщины) и длины увеличивает её резонансную частоту

26. Волна - это возмущение, распространяющееся с конечной скоростью в пространстве и несущее с собой энергию. Суть волнового движения состоит в переносе энергии без переноса вещества. По взаимоположению вектора возмущения и вектора скорости волны, волны подразделяются на продольные (направление вектора возмущения совпадает с направлением вектора скорости) и поперечные (вектор возмущения перпендикулярен вектору скорости).Уравнение плоской незатухающей бегущей волны. Бегущими называются волны которые переносят в пространстве энергию.S=So Sin(Wot-kt) – уравнение плоской бегущей волны

Уравнение плоской волны, распространяющейся вдоль положительного направления оси х

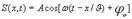
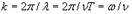
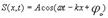
(S(x, t) — смещение точек среды с координатой х в момент времени /; А — амплитуда волны; ω— циклическая (круговая) частота; k — волновое число; λ—длина волны; v — фазовая скорость; Т— период колебаний; φ0 — начальная фаза колебаний)Упру́гие во́лны (звуковые волны) — волны, распространяющиеся в жидких, твёрдых и газообразных средах за счёт действия упругих сил.Энергия упругой волны. Найдем полную механическую энергию (5.8.2) для выделенного нами элемента упругой среды, в которой распространяются упругая продольная волна:

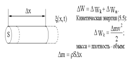Потенциальная энергия упругого деформированного стержня: 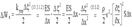.Полная энергия выделенного элемента объемом SΔx будет равна 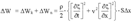Плотность энергии упругой волны

.

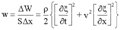Вектор плотности потока энергии (вектор Умова)

Характеризуется переносом энергии в волнах , совпадает по направлению с направлением скорости распространения волн и равен произведению обьемной плотности энергии на вектор скорости распространения волны.Вектор Умова можно определить черезвектороное произведение двух векторов:

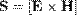,где E и H — векторы напряжённости электрического и магнитного полей соответствен

27. Сложение (Интерференция) волн — взаимное увеличение или уменьшениерезультирующей амплитуды двух или нескольких когерентных волн, одновременно распространяющихся в пространстве.^[1] Сопровождается чередованием максимумов и минимумов (пучностей) интенсивности в пространстве. Результат интерференции (интерференционная кар

Стоя́чая волна́ — колебания в распределённых колебательных системах с характерным расположением чередующихся максимумов (пучностей) и минимумов (узлов) амплитуды. Практически такая волна возникает приотражениях от преград и неоднородностей в результате наложения отражённой волны на падающую. При этом крайне важное значение имеет частота, фаза и коэффициент затухания волны в месте отражения.

Примерами стоячей волны могут служить колебания струны, колебания воздуха в органной трубе^[1]; в природе —волны Шумана.

Чисто стоячая волна, строго говоря, может существовать только при отсутствии потерь в среде^[2] и полном отражении волн от границы. Обычно, кроме стоячих волн, в среде присутствуют и бегущие волны, подводящие энергию к местам её поглощения или излучения.

Для демонстрации стоячих волн в газе используют трубу Рубенса.тина) зависит от разности фаз накладывающихся волн

28. Термодинамическая система — это любая область пространства, ограниченная действительными или воображаемыми границами, выбранными для анализа её внутренних термодинамических параметров.

Пространство, смежное с границей системы, называется внешней средой. У всех термодинамических систем есть среда, с которой может происходить обмен энергии и вещества.Границы термодинамической системы могут быть неподвижными или

подвижными.Системы могут быть большими или маленькими, в зависимости от границ.Система может существовать в вакууме или может содержать несколько фаз одного или более веществ. Термодинамические системы могут содержать сухой воздух и водяной пар (два вещества) или воду и водяной пар (две стадии одного и того же вещества). Однородная система состоит из одного вещества, одной его фазы или однородной смеси нескольких компонентов.Системы бывают изолированными (замкнутыми) или открытыми. В изолированной системе не происходит никаких обменных процессов с внешней средой. В открытой системе и энергия и вещество могут переходить из системы в среду и обратно.Состояние термодинамической системы определяется физическими свойствами вещества. Температура, давление, объем, внутренняя энергия, энтальпия и энтропия — это термодинамические величины, определяющие те или иные интегральные параметры системы. Данные параметры строго определяются лишь для систем, находящихся в состоянии термодинамического равновесия.Различают экстенсивные параметры состояния,пропорциональные массе термодинамической системы, и интенсивные параметры состояния, не зависящие от массы системы. К экстенсивным параметрам состояния. относятся: объём, Внутренняя энергия, Энтропия, Энтальпия, изохорно-изотермический потенциал Гиббсова энергия), изобарно-изометрический потенциал (Гельмгольцева энергия); к интенсивным параметрам состояния— давление, температура, концентрация, магнитная индукция и др. параметры состояния взаимосвязаны, так что равновесное состояние системы можно однозначно определить, установив значения ограниченного числа параметров состояния.В молекулярно-кинетической теории поль зуются идеализированной моделью идеаль ного газа, согласно которой:1) собственный объем молекул газа пренебрежимо мал по сравнению с объемом сосуда;2) между молекулами газа отсутству ют силы взаимодействия;

3) столкновения молекул газа между собой и со стенками сосуда абсолютно упругие.Модель идеального газа можно ис пользовать при изучении реальных газов, так как они в условиях, близких к нормальным (например, кислород гелий),

29. Закон равномерного распределения энергии по степеням свободы молекул. Основное уравнение молекулярно-кинетической теории газов.Число степеней свободы – это число независимых величин с помощью которых может быть задано положение системы. (1 атом =3 ст., 2 атома =5ст. 3 атома=6ст.)Закон Больцмана о равномерном распределении энергии по степеням свободы молекул: для статической системы, находящейся в состоянии термодинамического равновесия, на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная КТ/2 , а на каждую колебательную – КТ

средняя энергия приходящаяся на одну степень свободы:

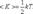У одноатомной молекулы i = 3, тогда для одноатомных молекул:

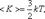для двухатомных молекул: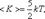

Таким образом, на среднюю кинетическую энергию молекулы, имеющей i-степеней свободы, приходится: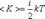

Молекулярно-кинетическая теория (сокращённо МКТ) — теория, рассматривающая строение вещества с точки зрения трёх основных приближенно верных положений:

1) все тела состоят из частиц, размером которых можно пренебречь: атомов, молекул и ионов;

2) частицы находятся в непрерывном хаотическом движении (тепловом);

3) частицы взаимодействуют друг с другом путём абсолютно упругих столкновений.Основное уравнение молекулярно-кинетической теории идеального газа:Уравнение, связывающее макроскопическую величину – давление с микроскопическими величинами, характеризующими молекулы.

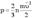p – давление газа, n - концентрация молекул, m₀ - масса молекулы.

30. Уравнение состояния идеального газа (иногда уравнение Клапейрона или уравнение Менделеева — Клапейрона) — формула, устанавливающая зависимость между давлением, молярным объёмом и абсолютной температурой идеального газа. Уравнение имеет вид:

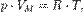
где

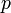— давление,

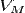— молярный объём,

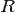— универсальная газовая постоянная

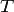— абсолютная температура,К.

31.Барометрическая формула — зависимость давления или плотности газа от высоты в поле тяжести.Для идеального газа, имеющего постоянную температуру 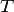и находящегося в однородном поле тяжести (во всех точках его объёма ускорение свободного падения 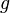одинаково), барометрическая формула имеет следующий вид:

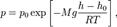
Распределением Больцмана

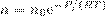(5)
Выражение (5) называется распределением Больцмана для внешнего потенциального поля. Из него видно, что при постоянной температуре плотность газа больше там, где меньше потенциальная энергия его молекул.

Закон распределения молекул идеального газа по скоростям, теоретически полученный Максвеллом в 1860 г. определяет, какое число dN молекул однородного (p = const) одноатомного идеального газа из общего числа N его молекул в единице объёма имеет при данной температуре Т скорости, заключенные в интервале от v до v + dv.

Для вывода функции распределения молекул по скоростям f(v) равной отношению числа молекул dN, скорости которых лежат в интервале v ÷ v + dv к общему числу молекул N и величине интервала dv

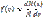
32.Средний путь, проходимый молекулой за единицу времени, численно равен 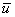. Поэтому средняя длина свободного пробега равна 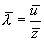. Для определения 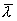вычислим сначала среднее число соударений 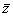выбранной молекулы с другими молекулами за единицу времени. Будем считать, что молекула после соударения продолжает двигаться по прямой со средней скоростью движения .

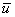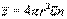
Это число 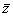и определяет среднее число соударений за единицу времени.

33.Явления (процессы), возникающие в газах при отклонении их от равновесия, называются явлениями переноса

Процесс установления внутри фаз равновесного распределения концентрации газовых молекул (а также молекул жидких и твёрдых тел) называется диффузией.

Процесс направленного переноса внутренней энергии (выравнивание температуры) называется теплопроводностью.

Процесс направленного переноса количества движения (связано с возникновением сил трения между слоями) называется внутренним трением.(Вязкостью)

34.Термодинамические процессы

Любое состояние равновесия рабочего тела можно охарактеризовать его параметрами. Если в результате взаимодействия с окружающей средой хотя бы один из параметров изменяется, то происходит термодинамический процесс. Ранее было дано определение равновесного процесса, т.е. такого идеального процесса, когда в любой момент времени система находится в равновесии с окружающей средой.

Работа 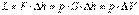, Дж.

Теплота

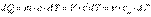
Виды теплоемкостей

Удельная теплоёмкость