Затухающие колебания материальной точки. Декремент затухания.
Все реальные колебательные системы являются диссипативными. Энергия механических колебаний такой системы постепенно расходуется на работу против сил трения, поэтому свободные колебания всегда затухают - их амплитуда постепенно уменьшается. Во многих случаях, когда отсутствует сухое трение, в первом приближении можно считать, что при небольших скоростях движения силы, вызывающие затухание механических колебаниях, пропорциональны скорости. Эти силы, независимо от их происхождения, называют силами сопротивления.
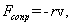 |
где r - коэффициент сопротивления, v - скорость движения. Запишем второй закон Ньютона для затухающих колебаний тела вдоль оси ОХ 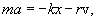
или 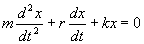 Перепишем это уравнение в следующем виде:
Перепишем это уравнение в следующем виде: 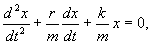
и обозначим: 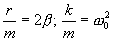
где 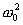 представляет ту частоту, с которой совершались бы свободные колебания системы при отсутствии сопротивления среды, т.е. при r = 0. Эту частоту называют собственной частотой колебания системы; β - коэффициент затухания. Тогда
представляет ту частоту, с которой совершались бы свободные колебания системы при отсутствии сопротивления среды, т.е. при r = 0. Эту частоту называют собственной частотой колебания системы; β - коэффициент затухания. Тогда
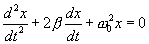 | (7.19) |
Будем искать решение уравнения (7.19) в виде
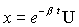
где U - некоторая функция от t.
Продифференцируем два раза это выражение по времени t и, подставив значения первой и второй производных в уравнение (7.19), получим 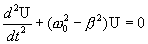
Решение этого, уравнения существенным образом зависит от знака коэффициента, стоящего при U. Рассмотрим случай, когда этот коэффициент положительный. Введем обозначение 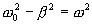 тогда С вещественным ω решением этого уравнения, как мы знаем, является функция
тогда С вещественным ω решением этого уравнения, как мы знаем, является функция 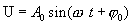
Таким образом, в случае малого сопротивления среды 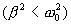 , решением уравнения (7.19) будет функция
, решением уравнения (7.19) будет функция
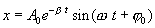 | (7.20) |
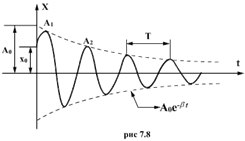
График этой функции показан на рис. 7.8. Пунктирными линиями показаны пределы, в которых находится смещение колеблющейся точки. Величину 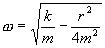 называют собственной циклической частотой колебаний диссипативной системы. Затухающие колебания представляют собой непериодические колебания, т.к, в них никогда не повторяются, например, максимальные значения смещения, скорости и ускорения. Величину
называют собственной циклической частотой колебаний диссипативной системы. Затухающие колебания представляют собой непериодические колебания, т.к, в них никогда не повторяются, например, максимальные значения смещения, скорости и ускорения. Величину 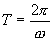 обычно называют периодом затухающих колебаний, правильнее - условным периодом затухающих колебаний,
обычно называют периодом затухающих колебаний, правильнее - условным периодом затухающих колебаний,
Натуральный логарифм отношения амплитуд смещений, следующих друг за другом через промежуток времени, равный периоду Т, называют логарифмическим декрементом затухания.
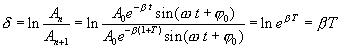
Обозначим через τ промежуток времени, за который амплитуда колебаний уменьшается в е раз. Тогда
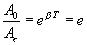
откуда
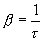
Следовательно, коэффициент затухания есть физическая величина, обратная промежутку времени τ, в течение которого амплитуда убывает в е раз. Величина τ называется временем релаксации.
Пусть N - число колебаний, после которых амплитуда уменьшается в е раз, Тогда
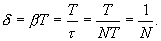
Следовательно, логарифмический декремент затухания δ есть физическая величина, обратная числу колебаний N, по истечению которого амплитуда убывает в е раз
