Уравнения Максвелла в интегральной и дифференцальной форме, их физический смысл
Уравне́ния Ма́ксвелла — система дифференциальных уравнений, описывающих электромагнитное поле и его связь с электрическими зарядами и токами в вакууме и сплошных средах. Вместе с выражением для силы Лоренца образуют полную систему уравнений классической электродинамики. Уравнения, сформулированные Джеймсом Клерком Максвеллом на основе накопленных к середине XIX века экспериментальных результатов, сыграли ключевую роль в развитии представлений теоретической физики и оказали сильное, зачастую решающее, влияние не только на все области физики, непосредственно связанные с электромагнетизмом, но и на многие возникшие впоследствии фундаментальные теории, предмет которых не сводился к электромагнетизму (одним из ярчайших примеров здесь может служить специальная теория относительности).
Уравнения Максвелла
!!!! Величины H, l, j, В, D – ВЕКТОРНЫЕ !!!!
Уравнения Максвелла в интегральной форме
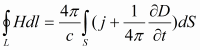
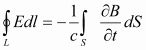
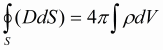
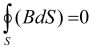
Уравнения Максвелла в дифференциальной форме
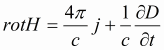
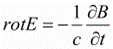
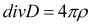
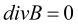
Н-напряжённость магнитного поля (в единицах СИ — А/м);
j- плотность электрического тока (плотность тока проводимости) (в единицах СИ — А/м²); в простейшем случае — случае тока, порождаемого одним типом носителей заряда, она выражается просто как , где — (средняя) скорость движения этих носителей в окрестности данной точки, — плотность заряда этого типа носителей (она в общем случае не совпадает с ); в общем случае это выражение надо усреднить по разным типам носителей;
B-магнитная индукция (в единицах СИ — Тл = Вб/м² = кг•с−2•А−1);
D- электрическая индукция (в единицах СИ — Кл/м²);
Уравнения Максвелла показывают, что источниками эл.поля могут быть либо эл.заряды, либо магнитные поля, меняющиеся во времени. Магнитные же поля могут возбуждаться либо движущими эл.зарядами(эл.токами), либо переменными электрическими полями.
Полная система уравнений Максвелла, особенно в дифференциальной форме (она справедлива для малой окрестности любой точки пространства) при задании начальных и граничных условий позволяет решать любые задачи классической макроскопической электродинамики. Она играет в электромагнетизме такую же роль, как законы Ньютона в механике.
Следствием теории Максвелла является существование электромагнитного поля в виде электромагнитных волн (ЭМВ). ЭМВ – распространяющееся в пространстве электромагнитное поле. В основе образования ЭМВ лежат взаимные превращения электрического и магнитного полей: переменное магнитное поле порождает в окружающем пространстве переменное электрическое поле и это изменяющееся электрическое поле также создаёт в окружающем пространстве переменное магнитное поле и т.д. Процесс образования переменных электрического и магнитного полей охватывает всё новые и новые области пространства – в пространстве распространяется ЭМВ
