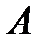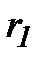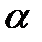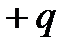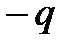Теорема Гаусса для вектора D
Принцип суперпозиции.
Напряжённость поля системы зарядов равна векторной сумме напряжённостей полей, которые создавал бы каждый из зарядов системы в отдельности. 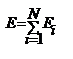
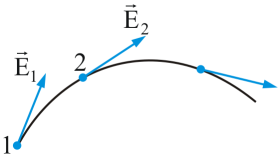 Для того чтобы описать электрическое поле, нужно задать вектор напряженности в каждой точке поля. Это можно сделать аналитически или графически. Для этого пользуютсясиловыми линиями – это линии, касательная к которым в любой точке поля совпадает с направлением вектора напряженности
Для того чтобы описать электрическое поле, нужно задать вектор напряженности в каждой точке поля. Это можно сделать аналитически или графически. Для этого пользуютсясиловыми линиями – это линии, касательная к которым в любой точке поля совпадает с направлением вектора напряженности  . Силовой линии приписывают определенное направление – от положительного заряда к отрицательному, или в бесконечность.
. Силовой линии приписывают определенное направление – от положительного заряда к отрицательному, или в бесконечность.
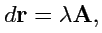 Чтобы получить уравнение векторных линий, будем рассматривать сами линии как кривую некоторой вектор-функцииr(t) скалярного аргумента. Тогда вектор dr будет направлен по касательной к векторной линии в точке с радиус-вектором r. Следовательно, он будет пропорционален вектору поля в этой точке:
Чтобы получить уравнение векторных линий, будем рассматривать сами линии как кривую некоторой вектор-функцииr(t) скалярного аргумента. Тогда вектор dr будет направлен по касательной к векторной линии в точке с радиус-вектором r. Следовательно, он будет пропорционален вектору поля в этой точке:
где 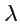 - некоторый коэффициент пропорциональности.В системе координат
- некоторый коэффициент пропорциональности.В системе координат
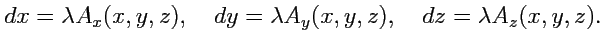 |
Исключив 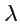 , получим систему
, получим систему 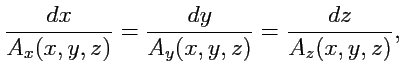
которая называется системой дифференциалных уравнений силовых линий.
3.Напряж. электростат. полей точечного заряда и произвольно заряженного тела. Однор. поле.
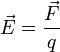 Напряжённость электри́ческого по́ля — векторная физическая величина, характеризующая электрическое поле в данной точке и численно равная отношению силы
Напряжённость электри́ческого по́ля — векторная физическая величина, характеризующая электрическое поле в данной точке и численно равная отношению силы 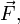 действующей на неподвижный пробный заряд, помещенный в данную точку поля, к величине этого заряда
действующей на неподвижный пробный заряд, помещенный в данную точку поля, к величине этого заряда 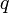 :
:
Напряжённость электрического поля точечного зарядаДля точечного заряда в электростатике верен закона Кулона
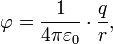 или
или 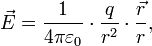
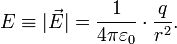
Получить этот результат проще всего исходя из теоремы Гаусса, учитывая сферическую симметрию: выбрать поверхность S в виде сферы с центром в точечном заряде, учесть, что направление 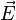 будет очевидно радиальным, а модуль этого вектора одинаков везде на выбранной сфере (так что E можно вынести за знак интеграла), и тогда, учитывая формулу для площади сферы радиуса r:
будет очевидно радиальным, а модуль этого вектора одинаков везде на выбранной сфере (так что E можно вынести за знак интеграла), и тогда, учитывая формулу для площади сферы радиуса r: 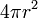 , имеем:
, имеем:
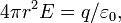 откуда сразу получаем ответ для E.
откуда сразу получаем ответ для E.
Ответ для 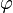 получается тогда интегрированием E:
получается тогда интегрированием E: 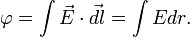
НЭП произвольного распределения зарядовПо принципу суперпозиции для напряженности поля совокупности дискретных источников имеем:
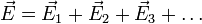 где каждое
где каждое 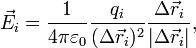
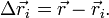
Подставив, получаем:
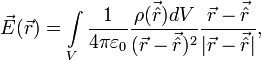
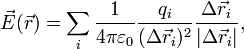
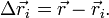 Для непрерывного распределения аналогично:
Для непрерывного распределения аналогично:
где V - область пространства, где расположены заряды (ненулевая плотность заряда), или всё пространство, 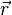 - радиус-вектор точки, для которой считаем
- радиус-вектор точки, для которой считаем 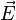 ,
, 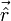 - радиус-вектор источника, пробегающий все точки области V при интегрировании, dV - элемент объема.
- радиус-вектор источника, пробегающий все точки области V при интегрировании, dV - элемент объема.
Электрическое поле, в котором напряженность одинакова по модулю и направлению в любой точке пространства, называется однородным электрическим полем.
Приблизительно однородным является электрическое поле между двумя разноименно заряженными плоскими металлическими пластинами. Линии напряженности в однородном электрическом поле параллельны друг другу
При равномерном распределении электрического заряда q по поверхности площади S поверхностная плотность заряда  постоянна и равна
постоянна и равна 
4.Потенц. электростат. поля. Эквипотенц. поверхн. Ур-е эквип. поверхн.
Электростатическим полем называется электрическое поле неподвижных в выбранной системе отсчета зарядов. Основными характеристиками электростатического поля являются напряженность и потенциал.Потенциал в какой либо точке эл.стат. поля есть физическая величина, определяемая потенциальной энергией положительного заряда, помещённого в эту точку. 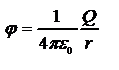
Разность потенциалов двух точек равна работе при перемещении единичного положительного заряда из точки 1 в точку 2. 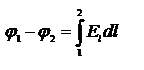
За нулевой потенциал часто удобно принимать потенциал бесконечно удаленной точки пространства.Потенциал – энергетическая характеристика электростатического поля. Если нулевой уровень потенциальной энергии системы зарядов условно выбрать на бесконечности, то выражение представляет собой работу внешней силы по перемещению единичного положительного заряда из бесконечности в рассматриваемую точку В: 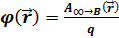 ;
;
Поверхность, во всех точках которой потенциал электрического поля имеет одинаковые значения, называется эквипотенциальной поверхностью.
Между двумя любыми точками на эквипотзенциальной поверхности разность потенциалов равна нулю, поэтому работа сил электрического поля при любом перемещении заряда по эквипотенциальной поверхности равна нулю. Это означает, что вектор силы Fэ в любой точке траектории движения заряда по эквипотенциальной поверхности перпендикулярен вектору скорости. Следовательно, линии напряженности электростатического поля перпендикулярны эквипотенциальной поверхности.
Если потенциал задан как функция координат (x, y, z), то уравнение эквипотенциальной поверхности имеет вид:
φ(x, y, z) = const
Эквипотенциальными поверхностями поля точечного электрического заряда являются сферы, в центре которых расположен заряд. Эквипотенциальные поверхности однородного электрического поля представляют собой плоскости, перпендикулярные линиям напряженности.
5.Связь между напряж.и потенциалом. Потенциалы полей точечного заряда и произв. заряж. тела. Потенц. однородного поля.
Найдем взаимосвязь между напряженностью электростатического поля, являющейся его силовой характеристикой, и потенциалом — энергетической характеристикой поля.
Работа по перемещению единичного точечного положительного заряда из одной точки в другую вдоль оси х при условии, что точки расположены бесконечно близко друг к равна А=Exdxq0. Та же работа равна A=(j1-j2)q0=-dj Приравняв оба выражения, можем записать
Ex=-дj/дx. Анлогично Ey=-дj/дy, Ez=-дj/z. Следовательно Е= Exi+ Eyj+ Ezk, где i, j, k — единичные векторы координатных осей х, у, z. Тогда 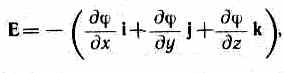
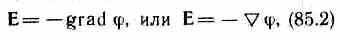 т. е. напряженность Е поля равна градиенту потенциала со знаком минус. Знак минус определяется тем, что вектор напряженности Е поля направлен в сторону убывания потенциала.
т. е. напряженность Е поля равна градиенту потенциала со знаком минус. Знак минус определяется тем, что вектор напряженности Е поля направлен в сторону убывания потенциала.
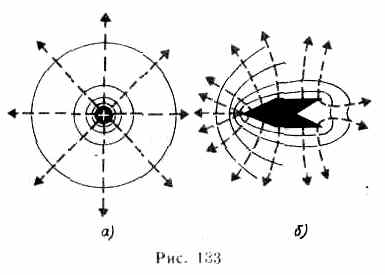 Для графического изображения распределения потенциала электростатического поля, как и в случае ноля тяготения, пользуются эквипотенциальными поверхностями — поверхностями, во всех точках которых потенциал j имеет одно и то же значение.
Для графического изображения распределения потенциала электростатического поля, как и в случае ноля тяготения, пользуются эквипотенциальными поверхностями — поверхностями, во всех точках которых потенциал j имеет одно и то же значение.
Если поле создается точечным зарядом, то его потенциал, согласно, j=(1/4pe0)Q/r. Таким образом, эквипотенциальные поверхности в данном случае — концентрические сферы.
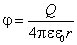 С другой стороны, линии напряженности в случае точечного заряда — радиальные прямые. Следовательно, линии напряженности в случае точечного заряда перпендикулярны эквипотенциальным поверхностям.
С другой стороны, линии напряженности в случае точечного заряда — радиальные прямые. Следовательно, линии напряженности в случае точечного заряда перпендикулярны эквипотенциальным поверхностям.
Потенциал поля точечного заряда Q в однородной изотропной среде с диэлектрической проницаемостью e :
Потенциал однородного поля:
φ = Wп / q = -Exx + C
Значение потенциала в данной точке зависит от выбора нулевого уровня для отсчёта потенциала. Этот уровень выбирают произвольно.
6. работа сил элктростат. поля по переносу точечного заряда. Циркуляция и ротор электростат. Поля
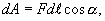 Элементарная работа, совершаемая силой F при перемещении точечного электрического зарядаqпр из одной точки электростатического поля в другую на отрезке пути dl , по определению равна
Элементарная работа, совершаемая силой F при перемещении точечного электрического зарядаqпр из одной точки электростатического поля в другую на отрезке пути dl , по определению равна
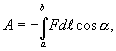 где
где 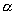 - угол между вектором силы F и направлением движения dl. Если работа совершается внешними силами, то dA=0. Интегрируя последнее выражение, получим, что работа против сил поля при перемещении пробного заряда qпр из точки “а” в точку “b” будет равна…
- угол между вектором силы F и направлением движения dl. Если работа совершается внешними силами, то dA=0. Интегрируя последнее выражение, получим, что работа против сил поля при перемещении пробного заряда qпр из точки “а” в точку “b” будет равна…
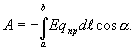 где
где 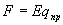 - кулоновская сила, действующая на пробный заряд qпр в каждой точке поля с напряженностью Е. Тогда работа…
- кулоновская сила, действующая на пробный заряд qпр в каждой точке поля с напряженностью Е. Тогда работа…
Пусть заряд 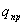 перемещается в поле заряда q из точки “а”, удалённой от q на расстоянии
перемещается в поле заряда q из точки “а”, удалённой от q на расстоянии 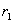 в точку “b”, удаленную от q на расстоянии
в точку “b”, удаленную от q на расстоянии 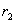 (рис 1.12).
(рис 1.12).
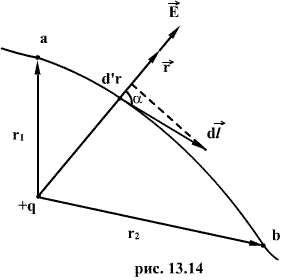 Как видно из рисунка
Как видно из рисунка 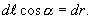 тогда получим
тогда получим
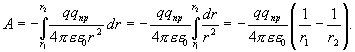
Как было сказано выше, работа сил электростатического поля, совершаемая против внешних сил, равна по величине и противоположна по знаку работе внешних сил, следовательно 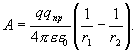
Работа электростатических сил по любому замкнутому контуру равна нулю. 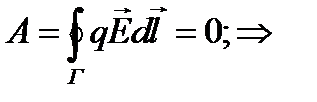
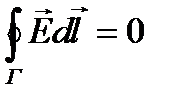 т.е. циркуляция электростатического поля по любому контуру равна нулю. Возьмем любую поверхность S, опирающуюся на контур Г.
т.е. циркуляция электростатического поля по любому контуру равна нулю. Возьмем любую поверхность S, опирающуюся на контур Г.
| S |
| Г |
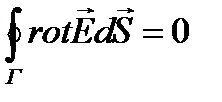 так как это для любой поверхности
так как это для любой поверхности S, то 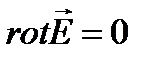
Существует тождество: 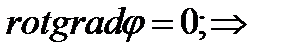
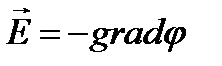 .
. 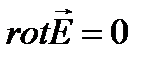 т.е. силовые линии электростатического поля не циркулируют в пространстве.
т.е. силовые линии электростатического поля не циркулируют в пространстве.
7. т-ма гауса для поля вектора E(r). Диверг. Электростат. Поля. Ур-е Пуасона для потенц. Электростат. Поля
Теорема Гаусса — основная теорема электродинамики, которая применяется для вычисления электрических полей. Она выражает связь между потоком напряжённости электрического поля сквозь замкнутую поверхность и зарядом в объёме, ограниченной этой поверхностью.
Поток вектора напряжённости электрического поля через любую, произвольно выбранную замкнутую поверхность пропорционален заключённому внутри этой поверхности электрическому заряду. 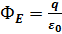 , где
, где 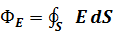 Для теоремы Гаусса справедлив принцип суперпозиции, то есть поток вектора напряжённости через поверхность не зависит от распределения заряда внутри поверхности.
Для теоремы Гаусса справедлив принцип суперпозиции, то есть поток вектора напряжённости через поверхность не зависит от распределения заряда внутри поверхности.
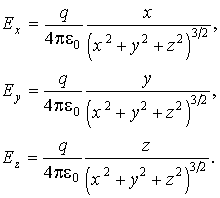 Теорема Гаусса для вектора напряженности электростатического поля
Теорема Гаусса для вектора напряженности электростатического поля 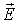 может быть сформулирована и в дифференциальной форме. Действительно, рассмотрим поле точечного электрического заряда
может быть сформулирована и в дифференциальной форме. Действительно, рассмотрим поле точечного электрического заряда 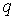 , расположенного в начале координат:
, расположенного в начале координат: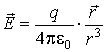 Из соотношения следует
Из соотношения следует
Легко проверить, что для 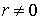 , то есть для точки наблюдения, в которой нет электрического заряда, справедливо соотношение:
, то есть для точки наблюдения, в которой нет электрического заряда, справедливо соотношение: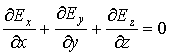 (1.55) Математическая операция в левой части соотношения (1.55) имеет специальное название "дивергенция векторного поля
(1.55) Математическая операция в левой части соотношения (1.55) имеет специальное название "дивергенция векторного поля 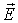 и специальное обозначение
и специальное обозначение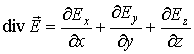
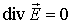
Уравнение Пуассона — эллиптическое ду в частных производных, которое, среди прочего, описывает электростатическое поле. Это уравнение имеет вид: 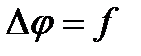
где Δ — оператор Лапласа или лапласиан, а f — действительная или комплексная функция на некотором многообразии.
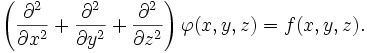 В трёхмерной декартовой системе координат уравнение принимает форму:
В трёхмерной декартовой системе координат уравнение принимает форму:
В декартовой системе координат оператор Лапласа записывается в форме 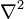 и уравнение Пуассона принимает вид:
и уравнение Пуассона принимает вид: 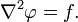 Если f стремится к нулю, то уравнение Пуассона превращается в ур-е Лапласа:
Если f стремится к нулю, то уравнение Пуассона превращается в ур-е Лапласа: 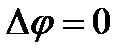
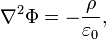 где Ф — электростатический потенциал,
где Ф — электростатический потенциал, 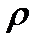 — объёмная плотность заряда, а
— объёмная плотность заряда, а 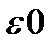 — диэлектрическая проницаемость вакуума.
— диэлектрическая проницаемость вакуума.
В области пространства, где нет непарной плотности заряда, имеем: 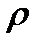 =0 и уравнение для потенциала превращается в уравнение Лапласа:
=0 и уравнение для потенциала превращается в уравнение Лапласа: 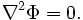
8.
Электростатическое поле — поле, созданное неподвижными в пространстве и неизменными во времени электрическими зарядами (при отсутствии электрических токов).
Если в пространстве имеется система заряженных тел, то в каждой точке этого пространства существует силовое электрическое поле. Оно определяется через силу, действующую на пробный заряд, помещённый в этом поле. Пробный заряд должен быть малым, чтобы не повлиять на характеристику электростатического поля.
В силу принципа суперпозиции потенциал всей совокупности зарядов равен сумме потенциалов, создаваемых в данной точке поля каждым из зарядов в отдельности: : 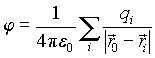
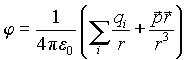 *
*
Величина 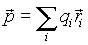 называется электрическим дипольным моментом системы зарядов.
называется электрическим дипольным моментом системы зарядов.
Электрич. дипольным моментом или просто дипольным моментомсистемы зарядов q i называется сумма произведений величин зарядов на их радиус-векторы.
Обычно дипольный момент обозначается латинской буквой d или латинской буквой p.
Дипольный момент имеет чрезвычайное значение в физике при изучении нейтральных систем. Действие электрического поля на нейтральную систему зарядов и электрическое поле создано нейтральной системой определяются в первую очередь дипольным моментом. Это, в частности, касается атомов и молекул.
Нейтральные системы зарядов с отличным от нуля дипольным моментом называют диполями.
Свойства:Всего определенный выше дипольный момент зависит от системы отсчета. Однако для нейтральной системы сумма всех зарядов равна нулю, поэтому зависимость от системы отсчета исчезает.
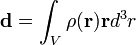 Самый диполь состоит из двух одинаковых по абсолютной величине, но противоположных по направлению зарядов + q и-q, которые находятся на определенном расстоянии r друг от друга. Дипольный момент тогда равна по абсолютной величине qr и направлен от положительного до отрицательного заряда. В случае непрерывного распределения заряда с плотностью
Самый диполь состоит из двух одинаковых по абсолютной величине, но противоположных по направлению зарядов + q и-q, которые находятся на определенном расстоянии r друг от друга. Дипольный момент тогда равна по абсолютной величине qr и направлен от положительного до отрицательного заряда. В случае непрерывного распределения заряда с плотностью 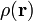 дипольный момент определяется интегрированием
дипольный момент определяется интегрированием
9. Диполь во внешнем электростат. Поле. Момент сил, действующий на диполь, потенц. Энергия диполя в однородном поле.
Электрическим диполем называют систему двух одинаковых по величине разноименных точечных зарядов 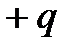 и
и 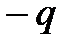 , расстояние между которыми значительно меньше расстояния до тех точек, в которых определяется поле системы. Прямая, проходящая через оба заряда, называется осью диполя. В соответствии с принципом суперпозиции потенциал поля в некоторой точке А равен:
, расстояние между которыми значительно меньше расстояния до тех точек, в которых определяется поле системы. Прямая, проходящая через оба заряда, называется осью диполя. В соответствии с принципом суперпозиции потенциал поля в некоторой точке А равен: 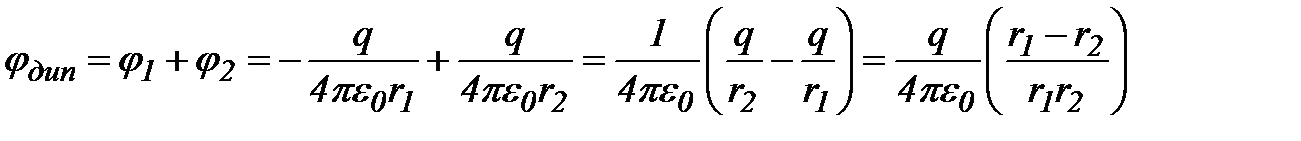 .
.
Пусть точка А выбрана так, что длина  намного меньше расстояний
намного меньше расстояний 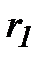 и
и 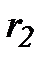 . В этом случае можно положить, что
. В этом случае можно положить, что 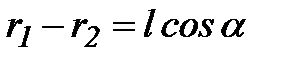 ;
; 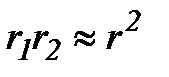 и формулу для потенциала диполя
и формулу для потенциала диполя 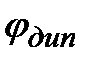 можно переписать:
можно переписать: 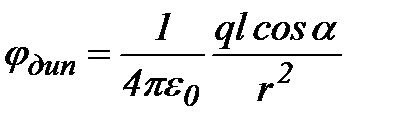
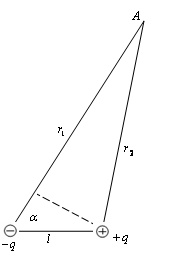 | где 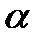 - угол между осью диполя и направлением к точке А, проведенным от диполя. Произведение - угол между осью диполя и направлением к точке А, проведенным от диполя. Произведение 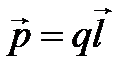 называется электрическим моментом диполя или дипольным моментом. Вектор называется электрическим моментом диполя или дипольным моментом. Вектор 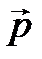 направлен по оси диполя от отрицательного заряда к положительному. Таким образом, произведение направлен по оси диполя от отрицательного заряда к положительному. Таким образом, произведение 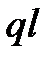 в формуле для в формуле для 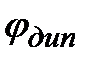 является дипольным моментом является дипольным моментом 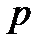 и соответственно: и соответственно: 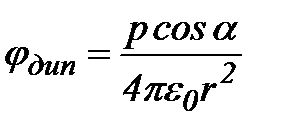 | |||||||
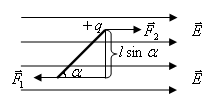 Момент сил, действующий на диполь во внешнем электрическом поле.
Момент сил, действующий на диполь во внешнем электрическом поле.
Поместим диполь в электрическое поле. Пусть направление диполя составляет с направлением вектора напряженности 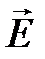 некоторый угол
некоторый угол 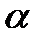 . На отрицательный заряд действует сила
. На отрицательный заряд действует сила 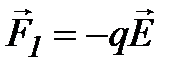 , направленная против поля, на положительный заряд действует сила
, направленная против поля, на положительный заряд действует сила 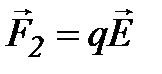 , направленная вдоль поля.Эти силы образуют пару сил с вращающим моментом:
, направленная вдоль поля.Эти силы образуют пару сил с вращающим моментом: 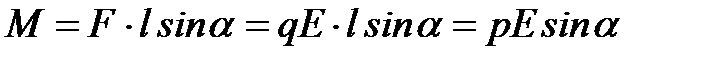 В векторном виде:
В векторном виде: 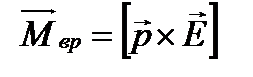
Диполь в однородном внешнем поле поворачивается под действием вращающего момента таким образом, чтобы сила, действующая на положительный заряд диполя, совпадала по направлению с вектором 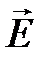 и осью диполя. Этому положению соответствует
и осью диполя. Этому положению соответствует 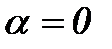 и
и 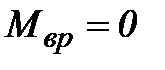
10. Диэлектрики в электростат. Поле. Векторы поляризованности и эл. Смещения. Диэл. Восприимч. И прониц. Среды. Связь между ними.
Диэлектрики – вещества, не имеющие практически свободных носителей заряда. Поэтому они не проводят ток, заряды не переходят, но поляризуются. диэлектрики – это вещества молекулярного строения, силы связи их зарядов внутри больше сил внешнего поля и они связаны, замкнуты внутри молекул и вовнешнем поле лишь частично сдвигаются, вызывая поляризацию.
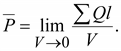 При наличии внешнего электростатического поля напряженностью
При наличии внешнего электростатического поля напряженностью 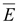 молекулы диэлектрика деформируются. Положительный заряд смещается по направлению внешнего поля, а отрицательный – в противоположном направлении, образуя диполь – связанный заряд. В диэлектриках, имеющих дипольные молекулы, их электрические моменты под влиянием внешнего поля частично ориентируются по направлению поля. У большинства диэлектриков направление вектора поляризованности
молекулы диэлектрика деформируются. Положительный заряд смещается по направлению внешнего поля, а отрицательный – в противоположном направлении, образуя диполь – связанный заряд. В диэлектриках, имеющих дипольные молекулы, их электрические моменты под влиянием внешнего поля частично ориентируются по направлению поля. У большинства диэлектриков направление вектора поляризованности 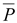 совпадает с направлением вектора напряженности внешнего поля, а направление вектора напряженности поляризованных зарядов
совпадает с направлением вектора напряженности внешнего поля, а направление вектора напряженности поляризованных зарядов 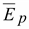 противоположно направлению вектора напряженности внешнего поля (от + Q к – Q).
противоположно направлению вектора напряженности внешнего поля (от + Q к – Q).
Вектор поляризованности определяют по геометрической сумме электрических моментов диполей в единице объема. Для большинства диэлектриков 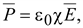 где k – относительная диэлектрическая восприимчивость.
где k – относительная диэлектрическая восприимчивость.
В электротехнических расчетах используется также вектор электрического смещения (индукции): 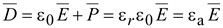 ,где
,где 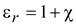 .Вектор
.Вектор 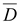 зависит как от свободных, так и от связанных зарядов.
зависит как от свободных, так и от связанных зарядов.
Диэлектрическая проницаемость среды ε показывает, во сколько раз сила взаимодействия двух электрических зарядов в среде меньше, чем в вакууме. Диэлектрическая восприимчивость ( поляризуемость ) вещества — физическая величина, мера способности вещества поляризоваться под действием электрического поля. Поляризуемость связана с диэлектрической проницаемостью ε соотн: 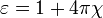 , или
, или 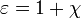 .
.
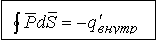 11.т-ма Гаусса для полей векторов P(r) и D(r) в интегр. И деф. Формах
11.т-ма Гаусса для полей векторов P(r) и D(r) в интегр. И деф. Формах
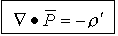 - теорема Гаусса для вектора
- теорема Гаусса для вектора 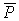 :поток вектора поляризованности
:поток вектора поляризованности 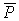 сквозь замкнутую поверхность
сквозь замкнутую поверхность 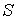 равна взятому с противоположным знаком избыточному связанному заряду диэлектрика в объеме, охватываемом поверхностью
равна взятому с противоположным знаком избыточному связанному заряду диэлектрика в объеме, охватываемом поверхностью 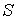 .
.
- дифференциальная форма:дивергенция вектора поляризованности 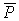 равна взятой с противоположным знаком объемной плотности избыточного связанного заряда в этой же точке.
равна взятой с противоположным знаком объемной плотности избыточного связанного заряда в этой же точке.
Точки, где 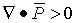 - источники поля
- источники поля 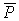 (из них линии поля расходятся), и наоборот, точки, где
(из них линии поля расходятся), и наоборот, точки, где 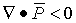 - стоки поля
- стоки поля 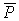 .
.
Плотность 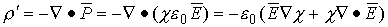 ;
; 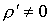 , когда:
, когда:
1) 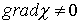 - диэлектрик неоднороден;2)
- диэлектрик неоднороден;2) 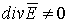 - поле неоднородно.
- поле неоднородно.
При поляризации однородного изотропного диэлектрика появляются только поверхностные связанные заряды, а объемные – нет.
Закон Био—Савара—Лапласа
Если по проводнику течет ток I, то в его окрестности создается магнитное поле, силовая характеристика которого 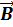 называется магнитной индукцией (величина
называется магнитной индукцией (величина 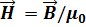 называется напряженностью магнитного поля). Магнитная индукция
называется напряженностью магнитного поля). Магнитная индукция 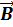 численно равна силе, действующей на проводник единичной длины, по которому течет электрический ток единичной силы и который расположен перпендикулярно к направлению однородного магнитного поля.
численно равна силе, действующей на проводник единичной длины, по которому течет электрический ток единичной силы и который расположен перпендикулярно к направлению однородного магнитного поля.
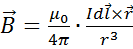
где 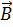 элементарная магнитная индукция, создаваемая элементом
элементарная магнитная индукция, создаваемая элементом 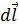 проводника с током
проводника с током 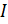 в точке пространства с радиусом-вектором
в точке пространства с радиусом-вектором 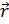 .
.
18.
Для расчета магнитных полей широко используется векторный магнитный потенциал. Его обозначают так 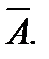 Это расчетная, искусственно введенная в расчет величина, которая плавно изменяется при переходе от одной точки к другой и такая, что
Это расчетная, искусственно введенная в расчет величина, которая плавно изменяется при переходе от одной точки к другой и такая, что 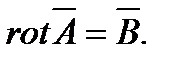 Основанием для представления
Основанием для представления 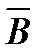 в виде
в виде 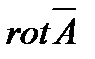 служит то обстоятельство, что дивергенция ротора любого вектора равна нулю, а в магнитном поле согласно принципа непрерывности магнитного потока
служит то обстоятельство, что дивергенция ротора любого вектора равна нулю, а в магнитном поле согласно принципа непрерывности магнитного потока 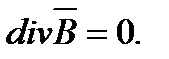
Уравнение, позволяющее рассчитывать 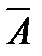 имеет вид
имеет вид 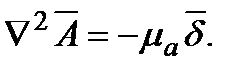 Это выражение получило название уравнения Пуассона для магнитного поля. Так как
Это выражение получило название уравнения Пуассона для магнитного поля. Так как 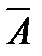 и
и 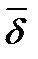 – это векторы, то их можно представить через проекции:
– это векторы, то их можно представить через проекции: 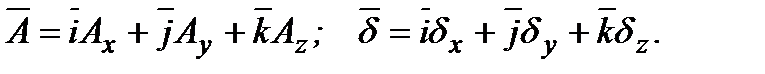 Тогда уравнение Пуассона распадается на три уравнения для скалярных величин:
Тогда уравнение Пуассона распадается на три уравнения для скалярных величин: 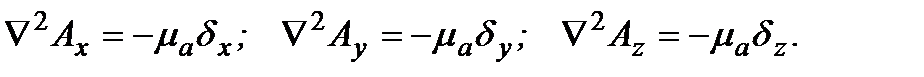 Именно последние три формулы используются в практических расчетах.
Именно последние три формулы используются в практических расчетах.
Рассмотрим как можно определить магнитный поток, используя ветор-потенциал магнитного поля. Магнитный поток,пронизывающий поверхность S, есть поток вектора В через эту поверхность 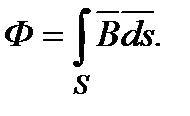 Поскольку
Поскольку 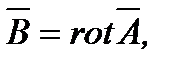 то
то 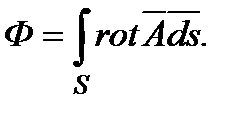 Согласно теореме Стокса
Согласно теореме Стокса 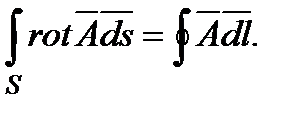 Следовательно,
Следовательно, 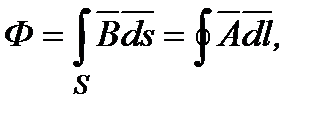 т.е. для определения магнитного потока, пронизывающего некоторую поверхность S, нужно вычислить циркуляцию вектор-потенциала по контуру, на который опирается данная поверхность S. Определение Ф через
т.е. для определения магнитного потока, пронизывающего некоторую поверхность S, нужно вычислить циркуляцию вектор-потенциала по контуру, на который опирается данная поверхность S. Определение Ф через 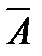 значительно проще чем через индукцию В.
значительно проще чем через индукцию В.
Теорема Гаусса для магнитного поля: магнитный поток через произвольную замкнутую поверхность равен нулю:
интеграл по замкнутому контуру с пределом S (вектор B*вектор dS)=0.
Теорема Гаусса для вектора B в дифференциальной форме: div(вектор B)=0.
Из закона Ампера (и закона Био-Савара-Лапласа) следует уравнение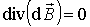 В силу принципа суперпозиции для индукции магнитного поля получаем фундаментальное соотношение для магнитного поля
В силу принципа суперпозиции для индукции магнитного поля получаем фундаментальное соотношение для магнитного поля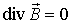
Таким образом, теорема Гаусса для векторного поля магнитной индукции в дифф. форме является непосредственным следствием закона Био-Савара-Лапласа.
Теорема Гаусса в интегральной форме отражает экспериментальный факт, что линии вектора B замкнуты. Уравнение дифференциальной формы эквивалентно уравнению интегральной и является математическим выражением того, что в природе нет магнитных «зарядов», на которых начинались бы или заканчивались бы линии магнитной индукции.
19.
На каждый носитель тока в проводнике действует магнитная сила. В результате магнитное поле действует на сам проводник с током с определенной cилой, называемой силой Ампера.
А. М. Ампер установил, что сила dF(векторное), с которой магнитное поле действует на элемент тока I*(вектор dl), помещенный во внешнее магнитное поле с индукцией B(векторное), равна:
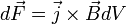
Эта формула выражает закон Ампера:
сила, действующая на элемент проводника с током в магнитном поле, равна произведению силы тока на векторное произведение элемента длины проводника на магнитную индукцию поля.
В частности, если магнитное поле однородно, а проводник линейный, то:
F=I*l*B*sin угла между вектором dl и вектором В.
Элементарную силу взаимодействия 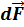 между элементами и
между элементами и 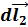 проводников, по которым протекают токи I1 и I2 можно определить из закона Ампера:
проводников, по которым протекают токи I1 и I2 можно определить из закона Ампера:
Направление силы Ампера определяют по правилу левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор B, а четыре вытянутых пальца расположить по направлению тока в проводнике, то отогнутый
большой палец покажет направление силы Ампера.
РАБОТА
Р 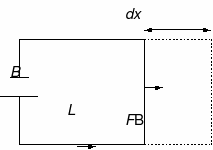 ассмотрим проводник длиной L с током I, помещенный в однородное внешнее магнитное поле, перпендикулярное плоскости контура. Проводник может свободно перемещаться.
ассмотрим проводник длиной L с током I, помещенный в однородное внешнее магнитное поле, перпендикулярное плоскости контура. Проводник может свободно перемещаться.
Сила, действующая на проводник равна: 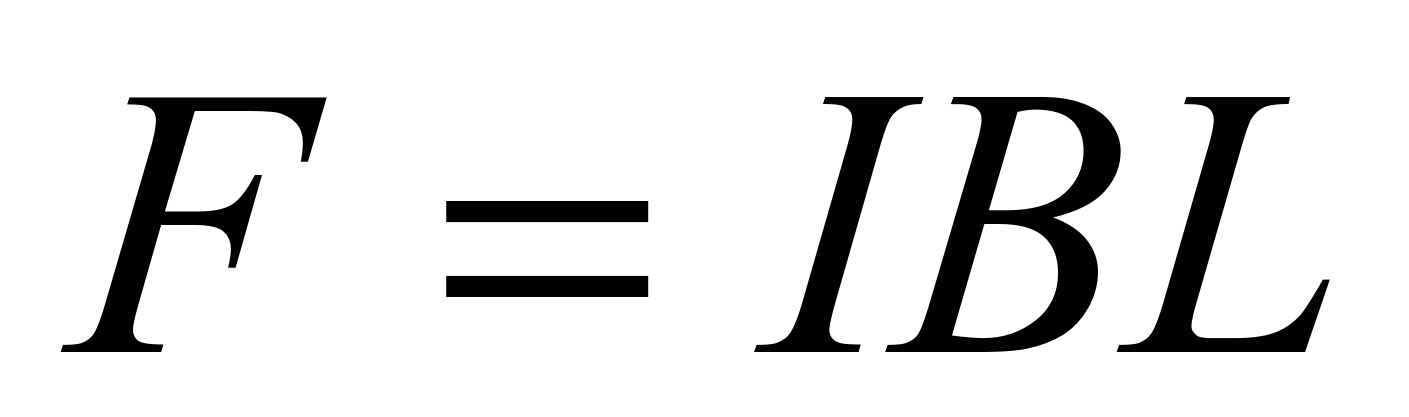
Найдем работу, совершаемую магнитным полем:
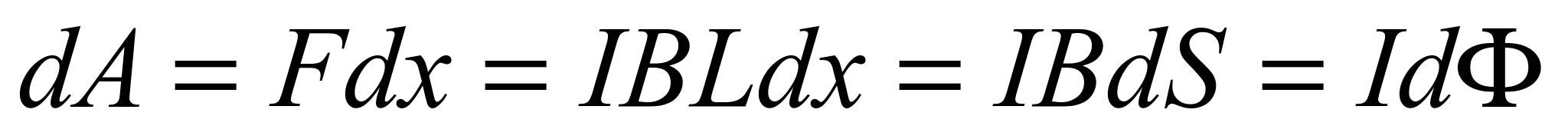
Таким образом, 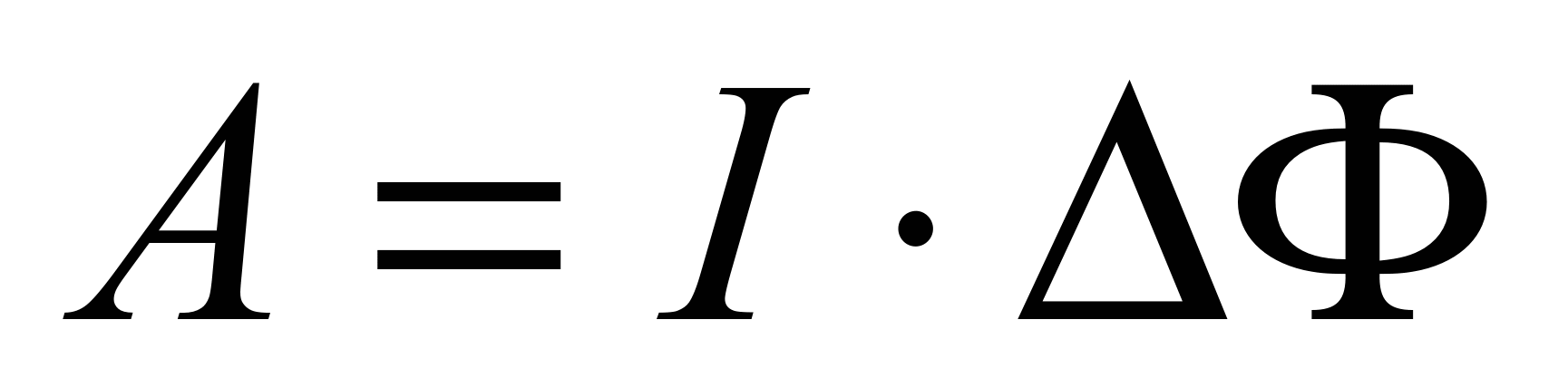
Работа по перемещению замкнутого контура с током в магнитном поле равна произведению силы тока в контуре на изменение магнитного потока, сцепленного с контуром.
Эта формула остается справедливой для контура любой формы в произвольном магнитном поле.
Магнитным моментом плоского замкнутого контура с током I называется: 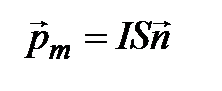 где S – площадь поверхности, ограниченной контуром, которую называют обычно поверхностью контура (или поверхностью, натянутой на контур); вектор n – единичный вектор нормали к плоскости контура. Векторы n и p мное направлены перпендикулярно плоскости контура по правилу правого винта
где S – площадь поверхности, ограниченной контуром, которую называют обычно поверхностью контура (или поверхностью, натянутой на контур); вектор n – единичный вектор нормали к плоскости контура. Векторы n и p мное направлены перпендикулярно плоскости контура по правилу правого винта
Со стороны внешнего магнитного поля на контур с током действует вращающий момент пары сил, который, как можно показать, определяется векторным произведением: 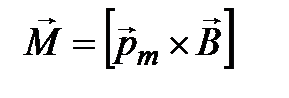
По определению векторного произведения скалярная величина момента равна: 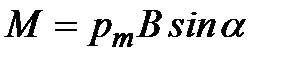
Формула справедлива для контура с током, находящегося в однородном магнитном поле, независимо от формы этого контура.
Работа при перемещении контура с током. Поскольку на проводник с током в магнитном поле действуют силы Ампера, то при движении проводника за счет источника тока совершается работа.
dA=I*dФ, где dA - работа при перемещении проводника с током, совершаемая силами магнитного поля, dФ - увеличение магнитного потока.
если рассматривать контур с током произвольной формы, который движется в магнитном поле, то, разбивая проводник на элементарные участки, работа по перемещению контура с током будет равна:
A=интеграл (I*dФ)=I*(Ф2-Ф1), где Ф1 и Ф2 – магнитный поток через площадь контура соответственно в начальном и конечном положениях.
Таким образом, работа по перемещению в постоянном магнитном поле замкнутого контура с током равна произведению силы тока в контуре на изменение его потокосцепления.
·Потенциальная энергия (механическая) контур с током в магнитное поле:
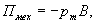 или
или 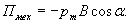
21.
Аналогично циркуляции вектора напряженности электростатического поля (см. § 83) введем циркуляцию вектора магнитной индукции. Циркуляцией вектора В по заданному замкнутому контуру
называется интеграл
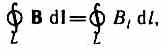
где dl — вектор элементарной длины контура, направленной вдоль обхода контура, В1=Вcosa — составляющая вектора В в направлении касательной к контуру (с учетом выбранного направления обхода), а — угол между векторами В и dl.
Закон полного тока для магнитного поля в вакууме (теорема о циркуляции вектора В): циркуляция вектора В по произвольному замкнутому контуру равна произведению магнитной постоянной m0 на алгебраическую сумму токов, охватываемых этим контуром:
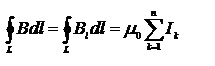 где n— число проводников с токами, охватываемых контуром L произвольной формы. Каждый ток учитывается столько раз, сколько раз он охватывается контуром. Положительным считается ток, направление которого связано с направлением обхода по контуру правилом правого винта; ток противоположного направления считается отрицательным.
где n— число проводников с токами, охватываемых контуром L произвольной формы. Каждый ток учитывается столько раз, сколько раз он охватывается контуром. Положительным считается ток, направление которого связано с направлением обхода по контуру правилом правого винта; ток противоположного направления считается отрицательным.
Неравенство нулю циркуляции вектора В свидетельствует о том, что поле вектора B непотенциально. Такое поле называется вихревым (соленоидальным).
Дифференциальная форма теоремы о циркуляции вектора B:
Теорема о циркуляции в дифференциальной форме имеет вид:
rot B = m0·j, (в "СИ")
rot B = [4p/c]·j. (в гауссовой системе)
Это уравнение имеет дифференциальный характер и справедливо для любой точки.
22.
Некоторые вещества в магнитном поле намагничиваются, то есть сами становятся источниками магнитного поля. Такие вещества называют магнетиками.
Магнитное состояние вещества можно охарактеризовать с помощью магнитного момента единицы объема. Эта величина называется вектор намагничивания M.
Напряжённость магни́тного по́ля (стандартное обозначение Н) –векторная физич. величина, равная разности вектора магнитной индукции B ивектора намагниченности M.В СИ: 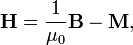 где
где 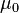 — магнитная постоянная.В СГС:
— магнитная постоянная.В СГС: 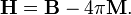
В общем случае, вектора M и H могут не совпадать. Это наблюдается для некоторого класса веществ, называемых анизотропными магнетиками (в них в них величина намагничения зависит еще и от направления внешнего поля в веществе). Если же вещество является изотропным магнетиком, то вектора M и H сонаправлены, то есть M=cH, где c - скалярная величина, называемая магнитной воспиимчивостью.
Тогда B=mH, где m=1+4pc- магнитная проницаемость вещества. Различные вещества очень сильно варьируются по своим магнитным свойствам.
Вещества, у которых m<1 называются диамагнетиками, те, у которых m>1 - парамагнетиками, а те, у которых m >> 1 - ферромагнетиками. Больше всего способны намагничиваться ферромагнетики.
По реакции на внешнее магнитное поле и характеру внутреннего магнитного упорядочения все вещества в природе можно подразделить на пять групп: диамагнетики(магнитная восприимчивость отрицательна и не зависит от напряженности внешнего магнитного поля), парамагнетики(вещества с положительной магнитной восприимчивостью, не зависящей от напряженности внешнего магнитного поля), ферромагнетики(вещества с большой положительной магнитной восприимчивостью (до 106), которая сильно зависит от напряженности магнитного поля и температуры), антиферромагнетики(возникает антипараллельная ориентация элементарных магнитных моментов) и фе