Вращательное движение. Частота вращения, период. Угловая скорость и угловое ускорение. Уравнение равномерного и равнопеременного вращательного движения
Вращательным движением твердого тела вокруг оси называется движение, при котором какие-либо его две точки остается неподвижными. Прямая, проходящая через эти точки, называется осью вращения. Все точки твердого тела при вращательном движении описывают окружности в плоскостях, перпендикулярных к оси вращения и с центрами, лежащими на этой оси. Тело, совершающее вращательное движение, имеет одну степень свободы, и его положение определяется углом φмежду проведенными через ось вращения неподвижной полуплоскостью и полуплоскостью, жестко связанной с телом и вращающейся вместе с ним.Для характеристики вращательного движения твердого тела вводят угловые характеристики:- угловое перемещение 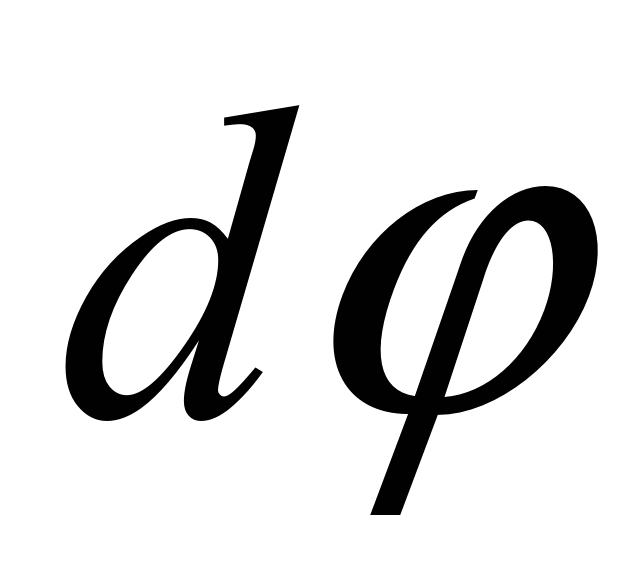 ;
;
- угловую скорость  ;- угловое ускорение
;- угловое ускорение  .
.
Угловым перемещением называется вектор 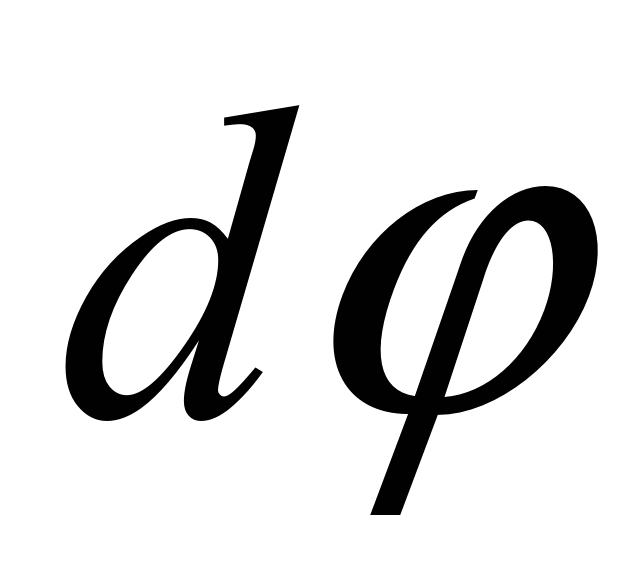 , модуль которого равен бесконечно малому углу поворота твердого тела при его вращений, а направление его определяется по правилу правого винта: если правый винт вращать в плоскости вращения тела по направлений его вращения, то перемещение его покажет направление
, модуль которого равен бесконечно малому углу поворота твердого тела при его вращений, а направление его определяется по правилу правого винта: если правый винт вращать в плоскости вращения тела по направлений его вращения, то перемещение его покажет направление 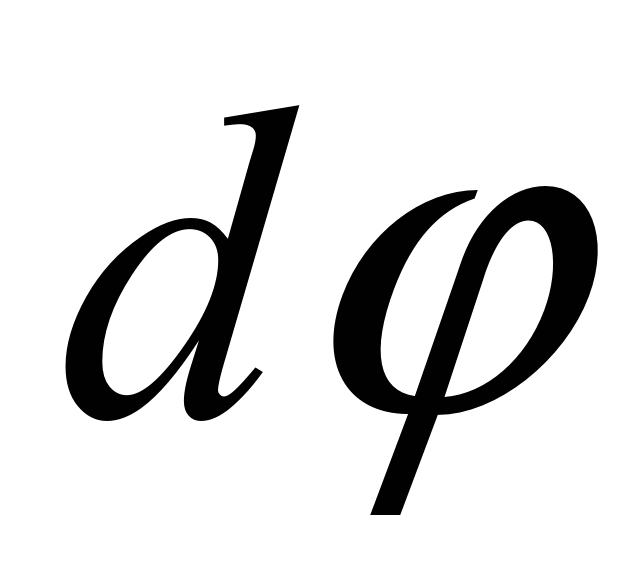 .Угловая скорость - векторная величина, характеризующая быстроту вращения твердого тела. Угловая скорость равна производной от угла поворота тела по времени. Радиан в секунду равен угловой скорости равномерного вращения тела, при котором оно поворачивается на угол 1 радиан, относительно оси вращения, за время 1с. Радиан на секунду в квадрате равен угловому ускорению равноускоренного вращения тела, ври котором за время 1сугловая скорость изменяется на
.Угловая скорость - векторная величина, характеризующая быстроту вращения твердого тела. Угловая скорость равна производной от угла поворота тела по времени. Радиан в секунду равен угловой скорости равномерного вращения тела, при котором оно поворачивается на угол 1 радиан, относительно оси вращения, за время 1с. Радиан на секунду в квадрате равен угловому ускорению равноускоренного вращения тела, ври котором за время 1сугловая скорость изменяется на 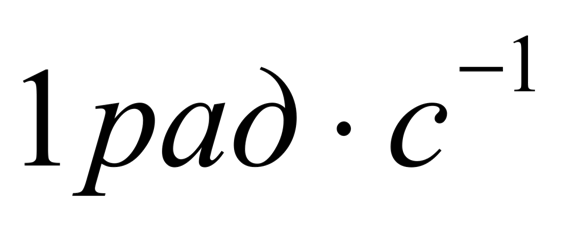 .Представление угловой скорости и углового ускорения в виде векторов оказывается чрезвычайно плодотворным, Это дает возможность во многих случаях получить большую наглядность, а так же упростить анализ движения.
.Представление угловой скорости и углового ускорения в виде векторов оказывается чрезвычайно плодотворным, Это дает возможность во многих случаях получить большую наглядность, а так же упростить анализ движения.
https://studopedia.ru/4_11065_lineynie-skorosti-i-uskorenie-svyaz-mezhdu-lineynimi-i-uglovimi-kinematicheskimi-velichinami-analogiya-formul-opisivayushchih-postupatelnoe-i-vrashchatelnoe-dvizhenie-tverdogo-tela.html
| Работа и кинетическая энергия |
 План лекции 1. Работа и кинетическая энергия. Теорема о кинетической энергии. Теорема Кёнига. 2. Консервативные и неконсервативные силы. 3. Потенциальная энергия. 1. Работа и кинетическая энергия По определению, элементарной работой силы План лекции 1. Работа и кинетическая энергия. Теорема о кинетической энергии. Теорема Кёнига. 2. Консервативные и неконсервативные силы. 3. Потенциальная энергия. 1. Работа и кинетическая энергия По определению, элементарной работой силы 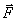 на бесконечно малом перемещении на бесконечно малом перемещении 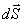 называется скалярное произведение этих двух векторов (рис. 6.1): называется скалярное произведение этих двух векторов (рис. 6.1): 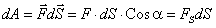 . (6.1) α — угол между векторами . (6.1) α — угол между векторами 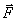 и и 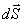 , FS = F × Cosα — проекция силы , FS = F × Cosα — проекция силы 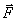 на направление перемещения на направление перемещения 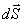 . Рис. 6.1 Работа силы — скалярная величина, которая может быть как положительной, так и отрицательной. Формально знак работы определяется знаком косинуса. Если . Рис. 6.1 Работа силы — скалярная величина, которая может быть как положительной, так и отрицательной. Формально знак работы определяется знаком косинуса. Если 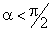 — Cosα > 0 и работа силы положительна. Сила, направленная в сторону противоположную смещению, совершает отрицательную работу. Если вектор силы образует с вектором перемещения или скорости прямой угол, то работа такой силы равна нулю. Так, работу не производит центростремительная сила при движении по круговой орбите, сила тяжести и сила реакции опоры при перемещении тела по горизонтальной поверхности. Для того чтобы вычислить работу на конечном участке траектории, нужно рассмотреть криволинейный интеграл вектора — Cosα > 0 и работа силы положительна. Сила, направленная в сторону противоположную смещению, совершает отрицательную работу. Если вектор силы образует с вектором перемещения или скорости прямой угол, то работа такой силы равна нулю. Так, работу не производит центростремительная сила при движении по круговой орбите, сила тяжести и сила реакции опоры при перемещении тела по горизонтальной поверхности. Для того чтобы вычислить работу на конечном участке траектории, нужно рассмотреть криволинейный интеграл вектора 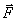 вдоль этого участка траектории: вдоль этого участка траектории: 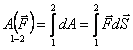 . (6.2) Если в процессе движения на тело действует система сил . (6.2) Если в процессе движения на тело действует система сил 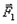 , , 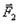 , …, , …, 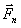 , то работа их равнодействующей равна алгебраической сумме работ каждой силы в отдельности. Показать это несложно. Спроецируем векторное уравнение , то работа их равнодействующей равна алгебраической сумме работ каждой силы в отдельности. Показать это несложно. Спроецируем векторное уравнение 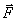 = = 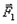 + + 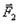 + … + + … + 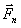 на направление элементарного перемещения на направление элементарного перемещения 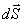 : FS = F1S + F2S + … + FnS. Теперь, умножив это уравнение на dS, получим искомый результат: FSdS = F1SdS + F2SdS + … + FnSdS, то есть: : FS = F1S + F2S + … + FnS. Теперь, умножив это уравнение на dS, получим искомый результат: FSdS = F1SdS + F2SdS + … + FnSdS, то есть: 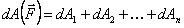 . Элементарная работа равнодействующей нескольких сил равна сумме элементарных работ этих сил. Это утверждение справедливо и для работ на конечном участке траектории: . Элементарная работа равнодействующей нескольких сил равна сумме элементарных работ этих сил. Это утверждение справедливо и для работ на конечном участке траектории: 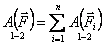 . В системе СИ работа измеряется в джоулях: 1 Дж = 1 Н × 1 м. Работа, выполняемая в единицу времени, называется мощностью: . В системе СИ работа измеряется в джоулях: 1 Дж = 1 Н × 1 м. Работа, выполняемая в единицу времени, называется мощностью: 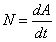 . Мощность — важная характеристика любого механизма. Единицей мощности является 1 Ватт. Это мощность устройства, которое ежесекундно совершает работу 1 Дж: 1 Вт = . Мощность — важная характеристика любого механизма. Единицей мощности является 1 Ватт. Это мощность устройства, которое ежесекундно совершает работу 1 Дж: 1 Вт = 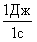 . Теперь обратимся к теореме о кинетической энергии. Работа силы при перемещении материальной точки равна изменению кинетической энергии этой точки. Докажем это положение. Материальная точка массы m движется под действием силы . Теперь обратимся к теореме о кинетической энергии. Работа силы при перемещении материальной точки равна изменению кинетической энергии этой точки. Докажем это положение. Материальная точка массы m движется под действием силы 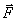 . Вычислим работу силы на участке 1-2 траектории. . Вычислим работу силы на участке 1-2 траектории.  . (6.3) Здесь мы воспользовались определением вектора силы . (6.3) Здесь мы воспользовались определением вектора силы 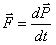 и кинематическим уравнением движения и кинематическим уравнением движения 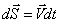 . Будем считать, что масса частицы в процессе движения не меняется, тогда: . Будем считать, что масса частицы в процессе движения не меняется, тогда: 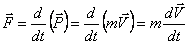 . Воспользуемся этим результатом в уравнении (6.3): . Воспользуемся этим результатом в уравнении (6.3): 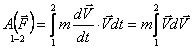 . (6.4) Теперь проделаем следующее очевидное преобразование: так как V2 = . (6.4) Теперь проделаем следующее очевидное преобразование: так как V2 = 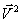 , то 2VdV = , то 2VdV = 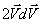 или или 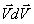 = VdV. Используя это равенство в уравнении (6.4), получим окончательный результат: = VdV. Используя это равенство в уравнении (6.4), получим окончательный результат: 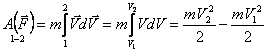 . (6.5) Величина . (6.5) Величина 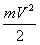 = Ек называется кинетической энергией материальной точки. Уравнение (6.5) является математической записью теоремы о кинетической энергии: работа силы, действующей на материальную точку, равна изменению её кинетической энергии. Важность и смысл введения понятия «работа силы» объясняется именно тем, что работа связана с изменением кинетической энергии тела: = Ек называется кинетической энергией материальной точки. Уравнение (6.5) является математической записью теоремы о кинетической энергии: работа силы, действующей на материальную точку, равна изменению её кинетической энергии. Важность и смысл введения понятия «работа силы» объясняется именно тем, что работа связана с изменением кинетической энергии тела: 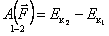 . (6.6) Кинетическая энергия системы тел принимается равной сумме кинетических энергий всех элементов системы. Теорема о кинетической энергии остаётся справедливой и для случая системы тел: работа всех сил, действующих на систему материальных тел, равна изменению кинетической энергии этой системы. Здесь важно подчеркнуть, что речь идёт о работе не только внешних сил, но и внутренних, то есть сил взаимодействия элементов системы друг с другом. Теорема Кёнига: скорость частицы и её кинетическая энергия зависят от системы отсчёта, в которой рассматривается движение частицы. В теореме Кёнига устанавливается правило преобразования кинетической энергии при переходе из одной системы отсчёта в другую. Рассмотрим сначала одну частицу. Пусть её кинетическая энергия в системе отсчёта S равна Ек. Какова будет её энергия . (6.6) Кинетическая энергия системы тел принимается равной сумме кинетических энергий всех элементов системы. Теорема о кинетической энергии остаётся справедливой и для случая системы тел: работа всех сил, действующих на систему материальных тел, равна изменению кинетической энергии этой системы. Здесь важно подчеркнуть, что речь идёт о работе не только внешних сил, но и внутренних, то есть сил взаимодействия элементов системы друг с другом. Теорема Кёнига: скорость частицы и её кинетическая энергия зависят от системы отсчёта, в которой рассматривается движение частицы. В теореме Кёнига устанавливается правило преобразования кинетической энергии при переходе из одной системы отсчёта в другую. Рассмотрим сначала одну частицу. Пусть её кинетическая энергия в системе отсчёта S равна Ек. Какова будет её энергия 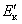 в системе отсчёта S’, движущейся со скоростью в системе отсчёта S’, движущейся со скоростью 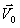 относительно S? Скорости частицы в этих двух системах связаны известным соотношением (смотри преобразования Галилея): относительно S? Скорости частицы в этих двух системах связаны известным соотношением (смотри преобразования Галилея): 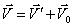 . Возведём это равенство в квадрат . Возведём это равенство в квадрат 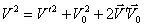 и домножим на и домножим на 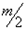  . Таким образом, устанавливается связь кинетических энергий частицы в разных системах отсчёта: . Таким образом, устанавливается связь кинетических энергий частицы в разных системах отсчёта: 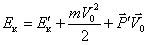 . (6.7) Обобщим этот результат на произвольную систему n материальных точек. Для каждой частицы системы можно записать уравнение (6.7). Теперь сложим все эти уравнения: . (6.7) Обобщим этот результат на произвольную систему n материальных точек. Для каждой частицы системы можно записать уравнение (6.7). Теперь сложим все эти уравнения: 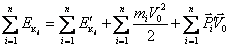 . (6.8) Здесь: . (6.8) Здесь: 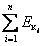 = К — кинетическая энергия системы материальных точек в системе отсчёта S. = К — кинетическая энергия системы материальных точек в системе отсчёта S. 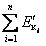 = = 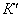 — кинетическая энергия той же системы в системе отсчёта S’. — кинетическая энергия той же системы в системе отсчёта S’. 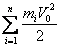 = = 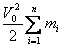 = = 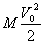 , где М = , где М = 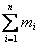 — масса системы. — масса системы. 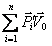 = = 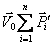 = = 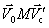 = = 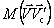 , где , где 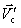 — скорость центра масс системы материальных точек в системе отсчёта S’. Таким образом, уравнению (6.8) можно придать такой вид: К= — скорость центра масс системы материальных точек в системе отсчёта S’. Таким образом, уравнению (6.8) можно придать такой вид: К= 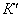 + + 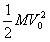 + + 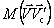 . (6.9) Если движущуюся систему отсчёта S’ связать с центром масс, то в такой системе . (6.9) Если движущуюся систему отсчёта S’ связать с центром масс, то в такой системе 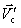 = 0. Формула теоремы Кёнига в этом случае упрощается: = 0. Формула теоремы Кёнига в этом случае упрощается: 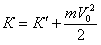 (6.10) Подводя итог, сформулируем теорему Кёнига. Кинетическая энергия системы материальных точек равна сумме кинетической энергии всей системы, мысленно сосредоточенной в её центре масс и движущейся вместе с ним и кинетической энергии той же системы в её относительном движении по отношению к поступательно движущейся системе координат с началом в центре масс. (6.10) Подводя итог, сформулируем теорему Кёнига. Кинетическая энергия системы материальных точек равна сумме кинетической энергии всей системы, мысленно сосредоточенной в её центре масс и движущейся вместе с ним и кинетической энергии той же системы в её относительном движении по отношению к поступательно движущейся системе координат с началом в центре масс. |
http://fizika-student.ru/rabota_i_kineticheskaya_energiya__22_243.html
