Геометрический смысл несобственного интеграла.
Несобственные интегралы.
Собственный – это определенный интеграл, в котором существенные 2 обстоятельства: конечный отрезок [a;b] и ограниченность интегрируемой функции.
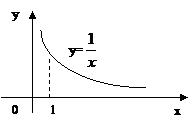 Но на практике часто бывает необходимо определить интеграл на бесконечном промежутке или проинтегрировать неограниченную функцию. (Но должна сохраняться преемственность).
Но на практике часто бывает необходимо определить интеграл на бесконечном промежутке или проинтегрировать неограниченную функцию. (Но должна сохраняться преемственность).
Одна из таких задач: найти площадь неограниченной фигуры.
1. Несобственные интегралы с бесконечными пределами. (Несобственные интегралы 1-го рода).
Пусть функция f(x) определена на интервале [a;+∞) и интегрируема на любом отрезке вида [a;b] для любого b≥a, так что интеграл 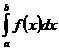 имеет смысл при b>a.
имеет смысл при b>a.
Определение.Если существует конечный предел
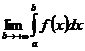 (1),
(1),
То этот предел называютнесобственным интегралом 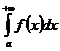 от функцииf(x) на интервале [a;+∞) и обозначают
от функцииf(x) на интервале [a;+∞) и обозначают 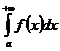 .
.
Т.о. по определению имеем: 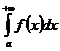 =
= 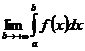
Если предел, стоящий в правой части равенства (1) существует и конечен, то несобственный интеграл называетсясходящимся (к данному пределу), в противном случае- расходящимся.
Т.о. при работе с несобственными интегралами выделяют 2 задачи:
1) исследование вопроса о сходимости данного интеграла;
2) вычисление значения интеграла, если он сходится.
Использование несобственных интегралов позволяет придать смысл такому понятию, как площадь полубесконечной или бесконечной фигуры.
Аналогично определяется несобственный интеграл на интервале (-∞;b]:
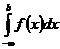 =
= 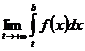 (2)
(2)
Введем понятие несобственного интеграла на интервале (-∞;+∞).
Пусть для некоторого числа а несобственные интегралы 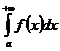 и
и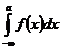 сходятся. Тогда
сходятся. Тогда
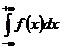 =
= 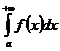 +
+ 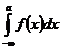 (3)
(3)
При этом интеграл 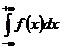 сходящийся.Если хотя бы один из интегралов
сходящийся.Если хотя бы один из интегралов 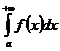 или
или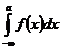 расходится, то не собственный интеграл
расходится, то не собственный интеграл 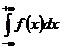 называетсярасходящимся.
называетсярасходящимся.
Это определение не зависит от выбора числа а.
Пример 1.I= 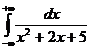 =
= 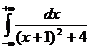 =
= 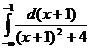 +
+ 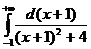
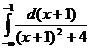 =
= 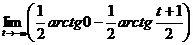 =0-
=0- 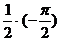 =
= 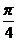
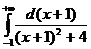 =
= 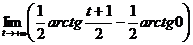 =
= 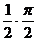 -0=
-0= 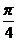
I= 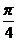 +
+ 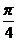 =
= 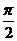
Пример 2. Изучим вопрос, при каких значениях показателя р>0 существует несобственный интеграл: 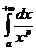 (a>0).
(a>0).
Пусть р¹1, тогда
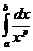 =
= 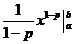 =
= 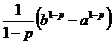
При b®¥ это выражение имеет пределом ¥, если р<1 или конечное число 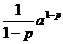 , если р>1.
, если р>1.
Если р=1, то 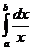 =
= 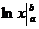 =
= 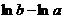
При b®¥ это выражение имеет пределом ¥.
Т.о. интеграл 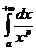 (a>0) при р>1 сходится и имеет значение
(a>0) при р>1 сходится и имеет значение 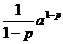 , а при р£1 – расходится.
, а при р£1 – расходится.
Признаки сходимости.
Теорема 1.Пусть b – конечное число такое, что b>a. Тогда несобственные интегралы  и
и 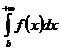 сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
Доказательство (б.д.?) Возьмем конечное число В такое, что В>b (ÞB>a).
Тогда 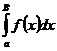 =
= 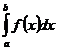 +
+ 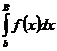 (4).
(4).
1) Пусть  - сходится Þ существует конечный предел
- сходится Þ существует конечный предел 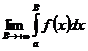 . Но тогда из (4) следует, что существует конечный предел
. Но тогда из (4) следует, что существует конечный предел 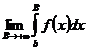 Þ
Þ 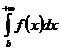 - сходится.
- сходится.
2) Пусть 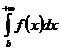 - сходится Þ существует конечный предел
- сходится Þ существует конечный предел 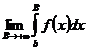 . Но тогда из (4) следует, что существует конечный предел
. Но тогда из (4) следует, что существует конечный предел 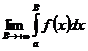 Þ
Þ  - сходится.
- сходится.
3) Пусть  - расходится. Покажем, что расходится и
- расходится. Покажем, что расходится и 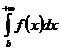 .
.
Допустим противное, что интеграл 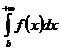 - сходится. Но тогда, по пункту 2), должен сходится и интеграл
- сходится. Но тогда, по пункту 2), должен сходится и интеграл  . Получили противоречие.
. Получили противоречие.
4) Пусть 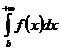 - расходится. Покажем, что расходится и
- расходится. Покажем, что расходится и  .
.
Допустим противное, что интеграл  - сходится. Но тогда, по пункту 1), должен сходится и интеграл
- сходится. Но тогда, по пункту 1), должен сходится и интеграл 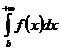 . Получили противоречие. Ч.т.д.
. Получили противоречие. Ч.т.д.
Теорема 2. Если f(x)³0 хотя бы для xÎ[b;+¥) (b³a), то для сходимости интеграла 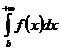 (а значит и интеграла
(а значит и интеграла  ) необходимо и достаточно, чтобы существовало число K>0 такое, что
) необходимо и достаточно, чтобы существовало число K>0 такое, что 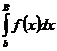 £К, для любого В (B>b).
£К, для любого В (B>b).
Доказательство. Интеграл 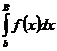 =j(В), т.е. представляет собой функцию от В, определенную в [b;+¥) и неубывающую там. Сходимость интеграла
=j(В), т.е. представляет собой функцию от В, определенную в [b;+¥) и неубывающую там. Сходимость интеграла 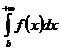 равносильна существованию конечного предела у функции j(В)=
равносильна существованию конечного предела у функции j(В)= 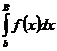 при В®+¥. Но для существования конечного предела при В®+¥ у функции j(В) необходимо и достаточно, чтобы существовало число K>0 такое, чтобы j(В)=
при В®+¥. Но для существования конечного предела при В®+¥ у функции j(В) необходимо и достаточно, чтобы существовало число K>0 такое, чтобы j(В)= 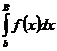 £К, для любого В (B>b). Ч.т.д.
£К, для любого В (B>b). Ч.т.д.
Теорема 3 (1-й признак сравнения несобственных интегралов).
Пусть хотя бы для хÎ[b;+∞) (b³a) функции f(x) и g(x) удовлетворяют условию 0≤f(x)≤g(x). Тогда:
1) из сходимости интеграла 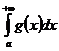 (5) следует сходимость интеграла
(5) следует сходимость интеграла  (6)
(6)
2) из расходимости интеграла  следует сходимость интеграла
следует сходимость интеграла 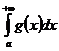 .
.
Доказательство (б.д.). Возьмем конечное число В такое, что В>b.
Тогда 0£ 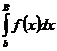 £
£ 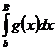 (7).
(7).
1) Пусть 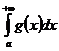 сходитсяÞ
сходитсяÞ 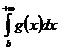 сходитсяÞ существует число K>0 такое, что
сходитсяÞ существует число K>0 такое, что 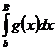 £К "В (В>b). Но тогда из (7) следует, что
£К "В (В>b). Но тогда из (7) следует, что 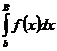 £К "ВÞпо теореме 2:
£К "ВÞпо теореме 2: 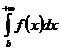 - сходитсяÞ
- сходитсяÞ  - сходится.
- сходится.
2) Пусть  - расходится. Нужно доказать, что расходится и
- расходится. Нужно доказать, что расходится и 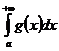 . Допустим противное, что
. Допустим противное, что 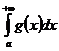 сходится. Тогда по пункту 1) должен сходится и
сходится. Тогда по пункту 1) должен сходится и  . Получили противоречие. Ч.т.д.
. Получили противоречие. Ч.т.д.
Часто при применении этого признака подынтегральную функцию сравнивают с функцией 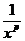 .
.
Пример 1.Исследовать сходимость интеграла 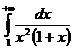
Сравним подынтегральную функцию f(x)= 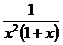 с функцией g(x)=
с функцией g(x)= 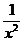 на [1;+∞). Очевидно, что на этом промежутке
на [1;+∞). Очевидно, что на этом промежутке 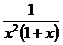 <
< 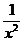 .
.
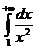 =
= 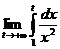 =
= 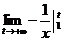 =
= 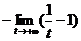 =-(0-1)=1
=-(0-1)=1
Т.к. интеграл 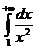 сходится, то и
сходится, то и 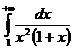 тоже сходится.
тоже сходится.
Пример 2. Исследовать на сходимость интеграл 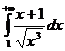 .
.
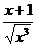 >
> 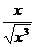 =
= 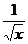
С другой стороны, 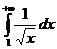 =
= 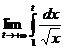 =
= 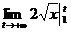 =2
=2 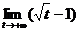 =+∞
=+∞
Следовательно, расходится и интеграл 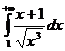 .
.
Теорема 4. (б.д.) (2-й признак сравнения).Пусть f(x)>0 и g(x)>0 хотя бы для хÎ[b,+¥) (b³а). Пусть существует конечный, отличный от нуля предел
l= 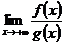 (l¹0, l¹¥).
(l¹0, l¹¥).
Тогда интегралы  и
и 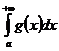 сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
Пример. Исследовать сходимость интеграла 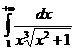 .
.
Функция f(x)= 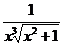 определена и непрерывна на промежутке [1;+¥)Þf(x) определена и непрерывна на промежутке [1,B], где В – любое число, удовлетворяющее условию B>1. Т.к. f(x)=
определена и непрерывна на промежутке [1;+¥)Þf(x) определена и непрерывна на промежутке [1,B], где В – любое число, удовлетворяющее условию B>1. Т.к. f(x)= 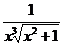 ~
~ 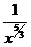 при х®+¥, то возьмем в качестве g(x)=
при х®+¥, то возьмем в качестве g(x)= 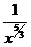 .
.
Тогда 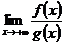 =
= 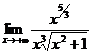 =1 (1¹0, 1¹¥).
=1 (1¹0, 1¹¥).
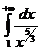 - сходится (р=
- сходится (р= 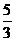 >1), следовательно и интеграл
>1), следовательно и интеграл 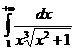 сходится.
сходится.
Признак Абеля-Дирихле.
Теорема.Пусть имеется несобственный интеграл 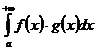 .
.
Пусть 1) f(x) определена и непрерывна на промежутке [a,+¥) и имеет там ограниченную первообразную F(x);
2) g(x) определена на промежутке [a,+¥) и имеет там непрерывную первообразную g¢(х);
3) g(x) монотонно убывает на [a,+¥) (Þg¢(х)£0, хÎ[a,+¥));
4) 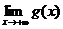 =0 (Þg(х)³0, хÎ[a,+¥)).
=0 (Þg(х)³0, хÎ[a,+¥)).
Тогда 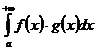 сходится.
сходится.
Пример.
Несобственные интегралы.
Собственный – это определенный интеграл, в котором существенные 2 обстоятельства: конечный отрезок [a;b] и ограниченность интегрируемой функции.
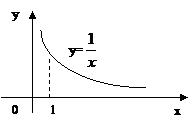 Но на практике часто бывает необходимо определить интеграл на бесконечном промежутке или проинтегрировать неограниченную функцию. (Но должна сохраняться преемственность).
Но на практике часто бывает необходимо определить интеграл на бесконечном промежутке или проинтегрировать неограниченную функцию. (Но должна сохраняться преемственность).
Одна из таких задач: найти площадь неограниченной фигуры.
1. Несобственные интегралы с бесконечными пределами. (Несобственные интегралы 1-го рода).
Пусть функция f(x) определена на интервале [a;+∞) и интегрируема на любом отрезке вида [a;b] для любого b≥a, так что интеграл 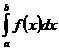 имеет смысл при b>a.
имеет смысл при b>a.
Определение.Если существует конечный предел
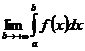 (1),
(1),
То этот предел называютнесобственным интегралом 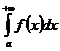 от функцииf(x) на интервале [a;+∞) и обозначают
от функцииf(x) на интервале [a;+∞) и обозначают 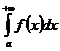 .
.
Т.о. по определению имеем: 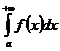 =
= 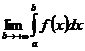
Если предел, стоящий в правой части равенства (1) существует и конечен, то несобственный интеграл называетсясходящимся (к данному пределу), в противном случае- расходящимся.
Т.о. при работе с несобственными интегралами выделяют 2 задачи:
1) исследование вопроса о сходимости данного интеграла;
2) вычисление значения интеграла, если он сходится.
Использование несобственных интегралов позволяет придать смысл такому понятию, как площадь полубесконечной или бесконечной фигуры.
Аналогично определяется несобственный интеграл на интервале (-∞;b]:
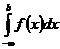 =
= 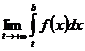 (2)
(2)
Введем понятие несобственного интеграла на интервале (-∞;+∞).
Пусть для некоторого числа а несобственные интегралы 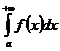 и
и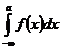 сходятся. Тогда
сходятся. Тогда
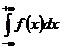 =
= 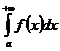 +
+ 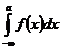 (3)
(3)
При этом интеграл 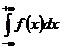 сходящийся.Если хотя бы один из интегралов
сходящийся.Если хотя бы один из интегралов 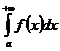 или
или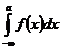 расходится, то не собственный интеграл
расходится, то не собственный интеграл 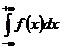 называетсярасходящимся.
называетсярасходящимся.
Это определение не зависит от выбора числа а.
Пример 1.I= 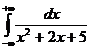 =
= 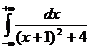 =
= 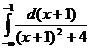 +
+ 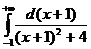
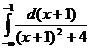 =
= 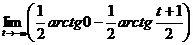 =0-
=0- 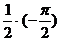 =
= 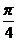
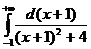 =
= 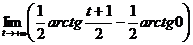 =
= 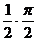 -0=
-0= 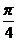
I= 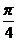 +
+ 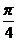 =
= 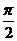
Пример 2. Изучим вопрос, при каких значениях показателя р>0 существует несобственный интеграл: 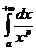 (a>0).
(a>0).
Пусть р¹1, тогда
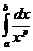 =
= 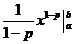 =
= 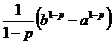
При b®¥ это выражение имеет пределом ¥, если р<1 или конечное число 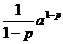 , если р>1.
, если р>1.
Если р=1, то 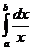 =
= 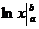 =
= 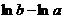
При b®¥ это выражение имеет пределом ¥.
Т.о. интеграл 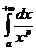 (a>0) при р>1 сходится и имеет значение
(a>0) при р>1 сходится и имеет значение 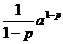 , а при р£1 – расходится.
, а при р£1 – расходится.
Геометрический смысл несобственного интеграла.
 При f(x)≥0 интеграл
При f(x)≥0 интеграл 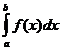 выражает площадь области, ограниченной кривой у=f(x), осью Ох и прямыми х=а и х=b. Несобственный интеграл
выражает площадь области, ограниченной кривой у=f(x), осью Ох и прямыми х=а и х=b. Несобственный интеграл 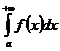 выражает площадь бесконечной области, заключенной между кривой у=f(x), осью Ох и прямой х=а. Аналогично определяет геометрический смысл интегралов
выражает площадь бесконечной области, заключенной между кривой у=f(x), осью Ох и прямой х=а. Аналогично определяет геометрический смысл интегралов 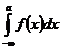 и
и 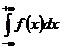 .
.
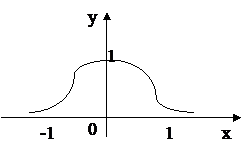
Пример.Найти площадь фигуры, ограниченной кривой у= 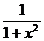 (локон Аньези) и осью Ох.
(локон Аньези) и осью Ох.
Функция непрерывна на всей числовой прямой.
Т.к. 
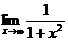 =0, то ось Ох является горизонтальной асимптотой. Следовательно, требуется найти конечную площадь бесконечной области, т.е. требуется вычислить несобственный интеграл
=0, то ось Ох является горизонтальной асимптотой. Следовательно, требуется найти конечную площадь бесконечной области, т.е. требуется вычислить несобственный интеграл 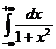 .
.
Т.к. функция у= 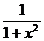 четная, то ее график симметричен относительно оси Оу, следовательно,
четная, то ее график симметричен относительно оси Оу, следовательно,
S= 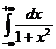 =2
=2 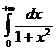 =2
=2 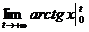 =2
=2 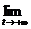 (arctg t-arctg 0)=2
(arctg t-arctg 0)=2 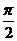 =π.
=π.
Во многих случаях бывает достаточно установить, сходится данный интеграл или расходится, и оценить его значение.
Признаки сходимости.
Теорема 1.Пусть b – конечное число такое, что b>a. Тогда несобственные интегралы  и
и 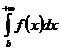 сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
Доказательство (б.д.?) Возьмем конечное число В такое, что В>b (ÞB>a).
Тогда 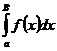 =
= 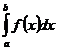 +
+ 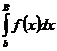 (4).
(4).
1) Пусть  - сходится Þ существует конечный предел
- сходится Þ существует конечный предел 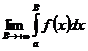 . Но тогда из (4) следует, что существует конечный предел
. Но тогда из (4) следует, что существует конечный предел 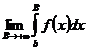 Þ
Þ 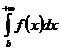 - сходится.
- сходится.
2) Пусть 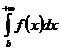 - сходится Þ существует конечный предел
- сходится Þ существует конечный предел 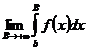 . Но тогда из (4) следует, что существует конечный предел
. Но тогда из (4) следует, что существует конечный предел 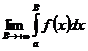 Þ
Þ  - сходится.
- сходится.
3) Пусть  - расходится. Покажем, что расходится и
- расходится. Покажем, что расходится и 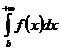 .
.
Допустим противное, что интеграл 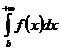 - сходится. Но тогда, по пункту 2), должен сходится и интеграл
- сходится. Но тогда, по пункту 2), должен сходится и интеграл  . Получили противоречие.
. Получили противоречие.
4) Пусть 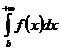 - расходится. Покажем, что расходится и
- расходится. Покажем, что расходится и  .
.
Допустим противное, что интеграл  - сходится. Но тогда, по пункту 1), должен сходится и интеграл
- сходится. Но тогда, по пункту 1), должен сходится и интеграл 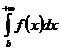 . Получили противоречие. Ч.т.д.
. Получили противоречие. Ч.т.д.
Теорема 2. Если f(x)³0 хотя бы для xÎ[b;+¥) (b³a), то для сходимости интеграла 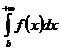 (а значит и интеграла
(а значит и интеграла  ) необходимо и достаточно, чтобы существовало число K>0 такое, что
) необходимо и достаточно, чтобы существовало число K>0 такое, что 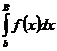 £К, для любого В (B>b).
£К, для любого В (B>b).
Доказательство. Интеграл 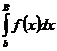 =j(В), т.е. представляет собой функцию от В, определенную в [b;+¥) и неубывающую там. Сходимость интеграла
=j(В), т.е. представляет собой функцию от В, определенную в [b;+¥) и неубывающую там. Сходимость интеграла 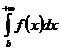 равносильна существованию конечного предела у функции j(В)=
равносильна существованию конечного предела у функции j(В)= 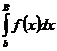 при В®+¥. Но для существования конечного предела при В®+¥ у функции j(В) необходимо и достаточно, чтобы существовало число K>0 такое, чтобы j(В)=
при В®+¥. Но для существования конечного предела при В®+¥ у функции j(В) необходимо и достаточно, чтобы существовало число K>0 такое, чтобы j(В)= 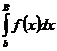 £К, для любого В (B>b). Ч.т.д.
£К, для любого В (B>b). Ч.т.д.
Теорема 3 (1-й признак сравнения несобственных интегралов).
Пусть хотя бы для хÎ[b;+∞) (b³a) функции f(x) и g(x) удовлетворяют условию 0≤f(x)≤g(x). Тогда:
1) из сходимости интеграла 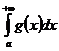 (5) следует сходимость интеграла
(5) следует сходимость интеграла  (6)
(6)
2) из расходимости интеграла  следует сходимость интеграла
следует сходимость интеграла 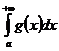 .
.
Доказательство (б.д.). Возьмем конечное число В такое, что В>b.
Тогда 0£ 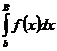 £
£ 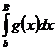 (7).
(7).
1) Пусть 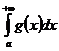 сходитсяÞ
сходитсяÞ 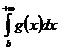 сходитсяÞ существует число K>0 такое, что
сходитсяÞ существует число K>0 такое, что 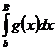 £К "В (В>b). Но тогда из (7) следует, что
£К "В (В>b). Но тогда из (7) следует, что 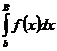 £К "ВÞпо теореме 2:
£К "ВÞпо теореме 2: 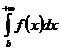 - сходитсяÞ
- сходитсяÞ  - сходится.
- сходится.
2) Пусть  - расходится. Нужно доказать, что расходится и
- расходится. Нужно доказать, что расходится и 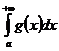 . Допустим противное, что
. Допустим противное, что 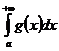 сходится. Тогда по пункту 1) должен сходится и
сходится. Тогда по пункту 1) должен сходится и  . Получили противоречие. Ч.т.д.
. Получили противоречие. Ч.т.д.
Часто при применении этого признака подынтегральную функцию сравнивают с функцией 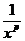 .
.
Пример 1.Исследовать сходимость интеграла 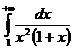
Сравним подынтегральную функцию f(x)= 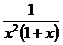 с функцией g(x)=
с функцией g(x)= 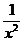 на [1;+∞). Очевидно, что на этом промежутке
на [1;+∞). Очевидно, что на этом промежутке 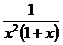 <
< 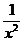 .
.
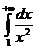 =
= 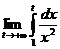 =
= 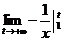 =
= 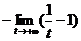 =-(0-1)=1
=-(0-1)=1
Т.к. интеграл 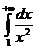 сходится, то и
сходится, то и 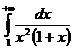 тоже сходится.
тоже сходится.
Пример 2. Исследовать на сходимость интеграл 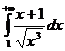 .
.
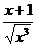 >
> 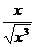 =
= 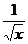
С другой стороны, 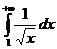 =
= 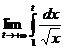 =
= 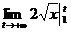 =2
=2 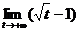 =+∞
=+∞
Следовательно, расходится и интеграл 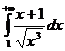 .
.
Теорема 4. (б.д.) (2-й признак сравнения).Пусть f(x)>0 и g(x)>0 хотя бы для хÎ[b,+¥) (b³а). Пусть существует конечный, отличный от нуля предел
l= 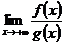 (l¹0, l¹¥).
(l¹0, l¹¥).
Тогда интегралы  и
и 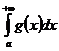 сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
Пример. Исследовать сходимость интеграла 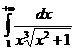 .
.
Функция f(x)= 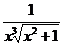 определена и непрерывна на промежутке [1;+¥)Þf(x) определена и непрерывна на промежутке [1,B], где В – любое число, удовлетворяющее условию B>1. Т.к. f(x)=
определена и непрерывна на промежутке [1;+¥)Þf(x) определена и непрерывна на промежутке [1,B], где В – любое число, удовлетворяющее условию B>1. Т.к. f(x)= 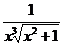 ~
~ 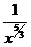 при х®+¥, то возьмем в качестве g(x)=
при х®+¥, то возьмем в качестве g(x)= 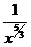 .
.
Тогда 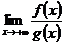 =
= 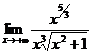 =1 (1¹0, 1¹¥).
=1 (1¹0, 1¹¥).
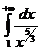 - сходится (р=
- сходится (р= 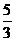 >1), следовательно и интеграл
>1), следовательно и интеграл 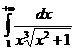 сходится.
сходится.
