Механический смысл определенного интеграла.

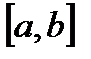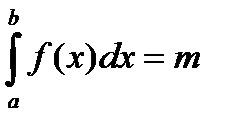Если подынтегральная функция непрерывна и неотрицательна на , то есть масса неоднородного стержня 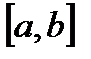с плотностью .

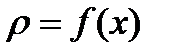5.3. Теорема существования определенного интеграла.

Если 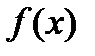непрерывна на отрезке 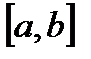, то 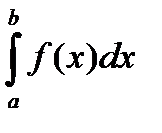существует.

5.4. Свойства определенного интеграла.

1)

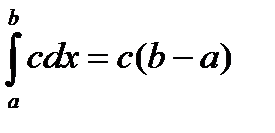
2)

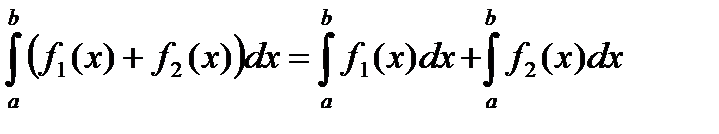
3) Постоянный множитель можно выносить за знак интеграла.

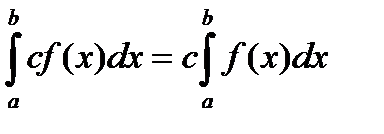, с=const.

4)

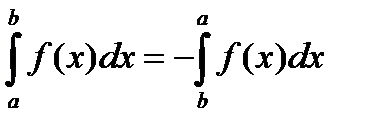
5)

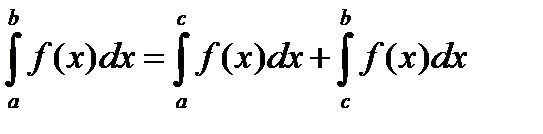
6)

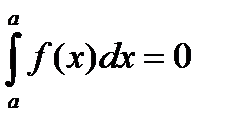
7) Если 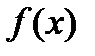знакопостоянна на 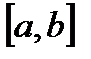, то 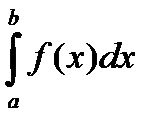имеет тот же знак, что и .

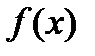8) Если 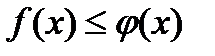, , 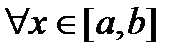то .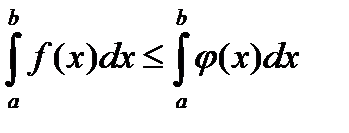

9) Теорема об оценке интеграла.

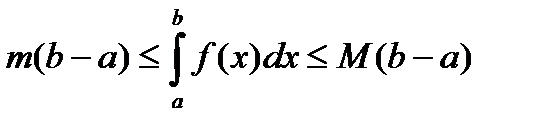, где m и M – соответственно наименьшее и наибольшее значения 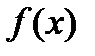на .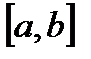

Замечание: свойства 2, 3, 4, 5, 7, 8, 9 справедливы, если соответствующие интегралы существуют.

10) Теорема о среднем.

Если 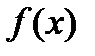непрерывна на 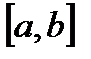, то существует точка 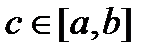, для которой справедливо равенство .

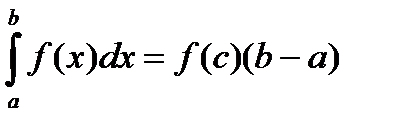Доказательство.

Так как 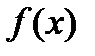непрерывна на отрезке 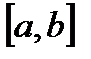, то она на этом отрезке достигает свои наименьшее и наибольшее значения и принимает все промежуточные значения между наименьшим и наибольшим значениями.

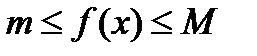, тогда по теореме об оценке интеграла имеем:

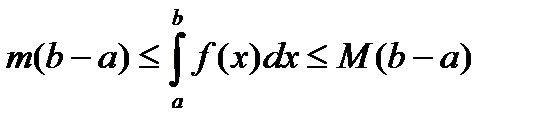, т.к. по условию 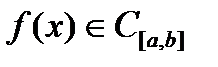и 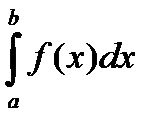существует.

В последних неравенствах все части неравенств поделим на (b-a), в результате получим:

.

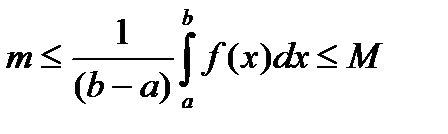Т.к. 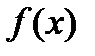принимает все промежуточные значения между m и M, то 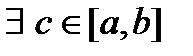, в которой 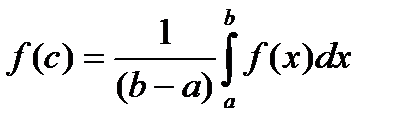. Теорема доказана.

Выражение 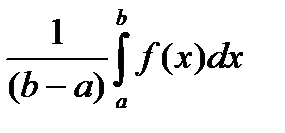называется средним значением функции 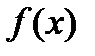на .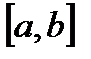

Лекция 6.

Тема: Интеграл с переменным верхним пределом. Формула Ньютона-Лейбница. Интегрирование по частям и заменой переменной в определенном интеграле.

6.1. Интеграл с переменным верхним пределом.

Пусть 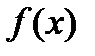непрерывная функция на отрезке 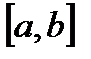. Рассмотрим интеграл 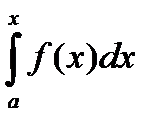, где верхний предел 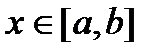. Верхний предел x и x под знаком интеграла разные и имеют разный смысл. Верхний предел x является произвольной фиксированной точкой отрезка 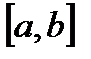, а x под знаком интеграла является переменной, которая изменяется от a до верхнего предела x. Интеграл 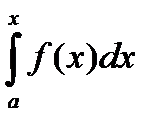называется интегралом с переменным верхним пределом, т.к. верхний предел x может принимать любое значение из отрезка 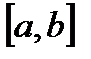. По условию 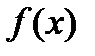непрерывна на любом отрезке 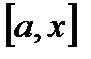, , 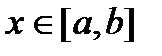то по теореме существования интеграл 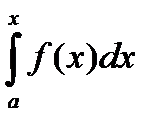существует для любого 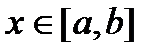, поэтому 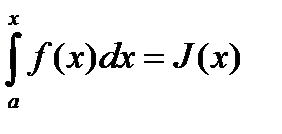является функцией от x.

Далее покажем, что функция 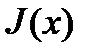является дифференцируемой функцией.

Теорема. Если 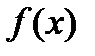непрерывна на отрезке 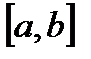, то производная от интеграла с переменным верхним пределом равна подынтегральной функции, т.е. 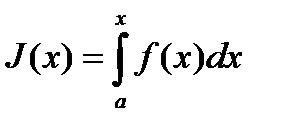является первообразной для подынтегральной функции на ,

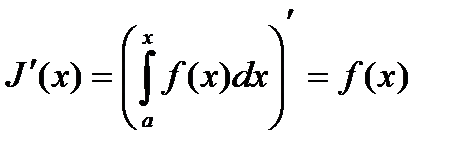
Доказательство.

По определению производной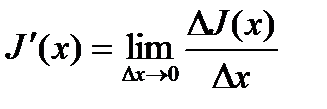

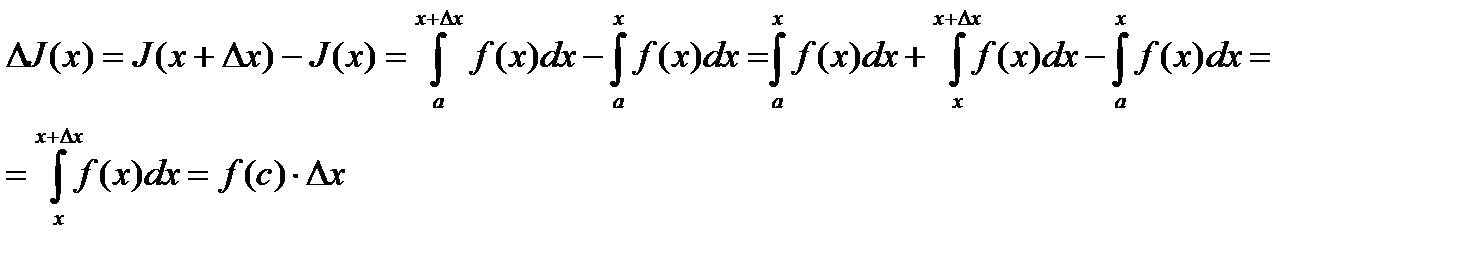
где с расположено между 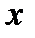и .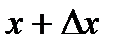

Последнее равенство имеет место в силу теоремы о среднем. Подставляя вместо 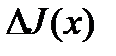полученное выражение, будем иметь

.

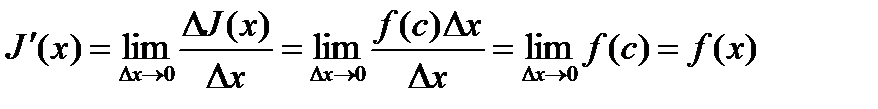Точка с расположена между 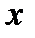и 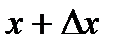, поэтому 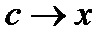при 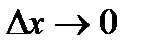. Так как 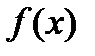непрерывна в точке x, то . ▼

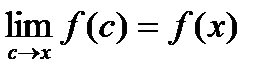6.2. Формула Ньютона-Лейбница.

Теорема. Справедлива формула 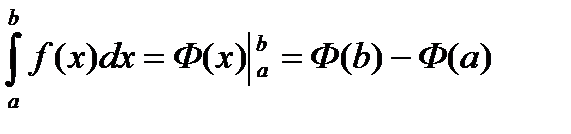, где Ф(x) какая-либо первообразная для подынтегральной функции .

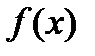Доказательство.

Рассмотрим интеграл с переменным верхним пределом 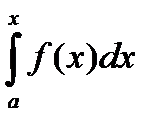. Этот интеграл является первообразной для функции 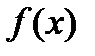. Пусть 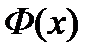– произвольная другая первообразная для 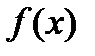. Две различные первообразные для функции 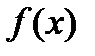различаются на константу. Поэтому 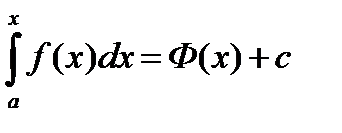. Положим верхний предел 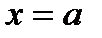, тогда получим: 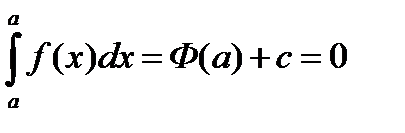, отсюда 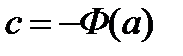, 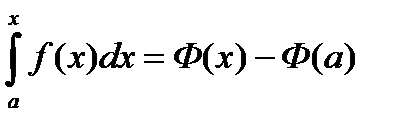. В последнем интеграле вместо верхнего предела x подставим 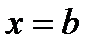, тогда получим: . ▼

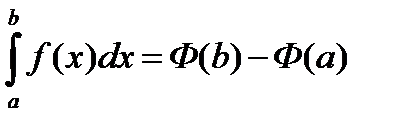Пример. Вычислить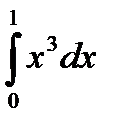

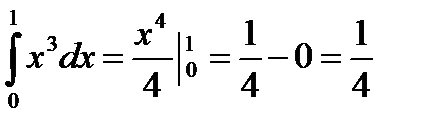
6.3. Интегрирование по частям в определенном интеграле.

Теорема. Справедлива формула .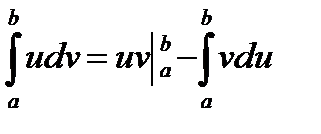

Доказательство. Имеем: .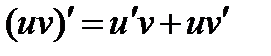

Почленно проинтегрируем последнее равенство

. ▼

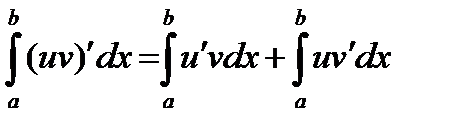
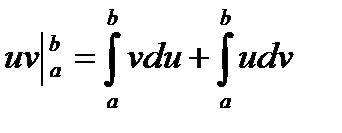
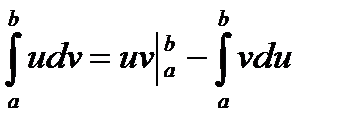Пример. Вычислить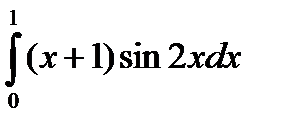

.

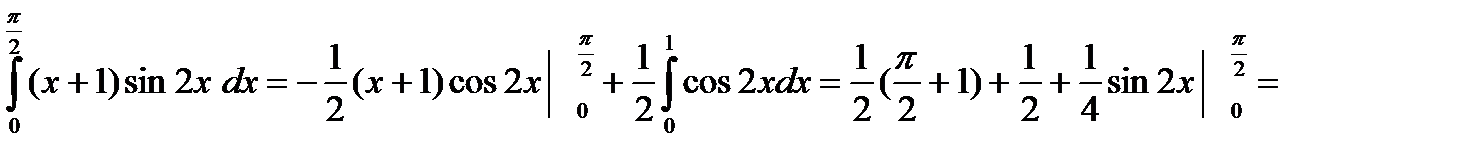
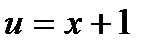
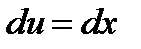
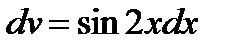
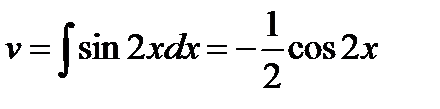
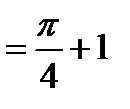Пример. Вычислить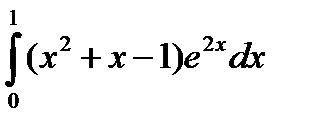

;

;

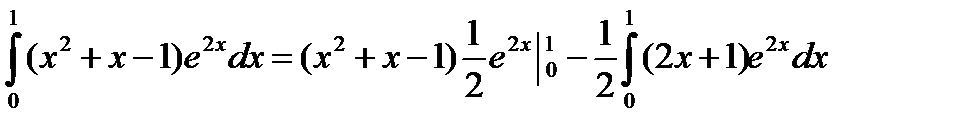
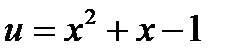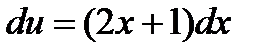
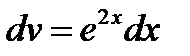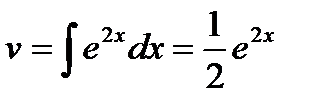
К последнему интегралу применим еще раз формулу интегрирование по частям.

;

;

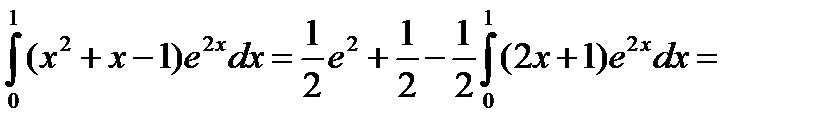
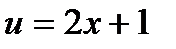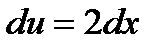
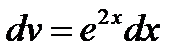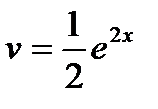
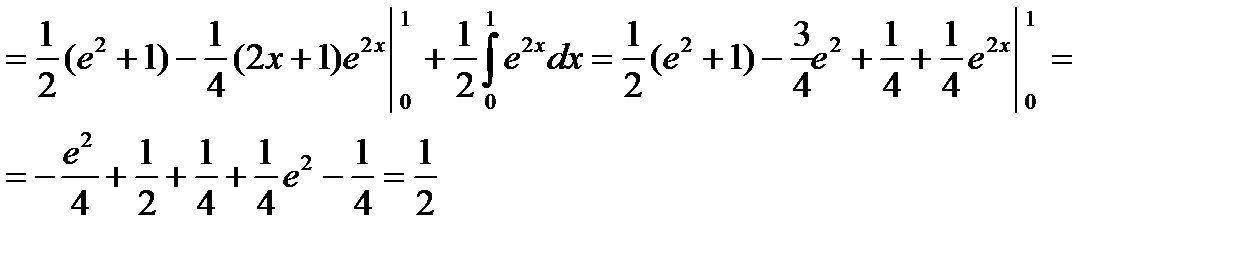
Пример. Вычислить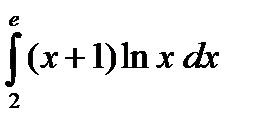

;

;

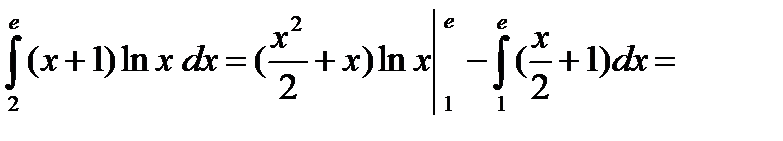
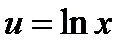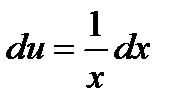
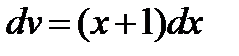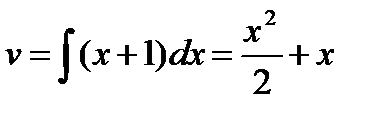
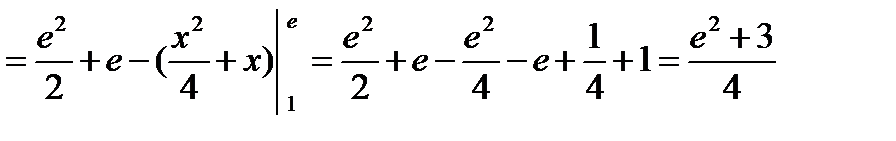
6.4. Замена переменной в определенном интеграле.

Пусть 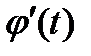непрерывна на отрезке 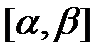и 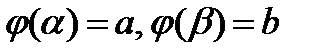, а функция 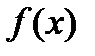непрерывна на отрезке .

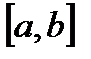Справедлива формула

.

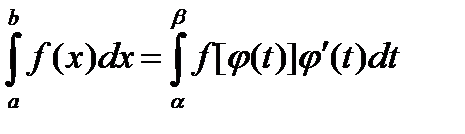Доказательство. Так как 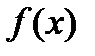непрерывна на 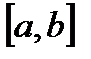, то она на этом отрезке имеет первообразную, которую обозначим .

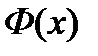Функция 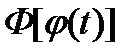является первообразной для функции 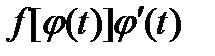на отрезке .

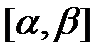В самом деле, применяя правило дифференцирования сложной функции, получим: 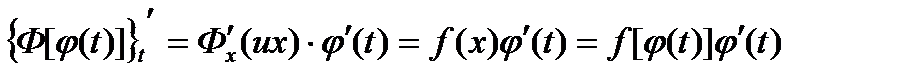, где .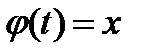

Используя формулу Ньютона-Лейбница, получим: . ▼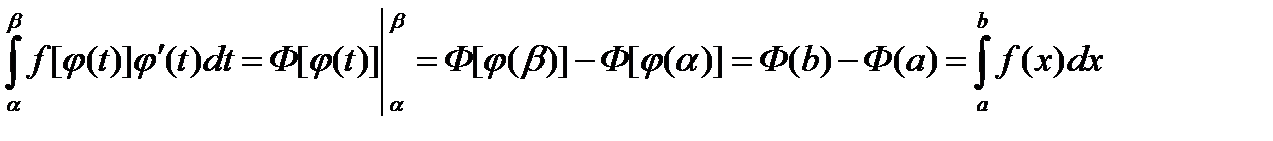

Пример. Вычислить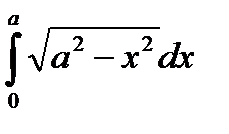

Сделаем замену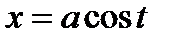

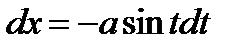
Если 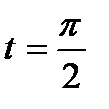, то 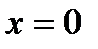, если 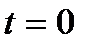, то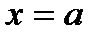

Следовательно,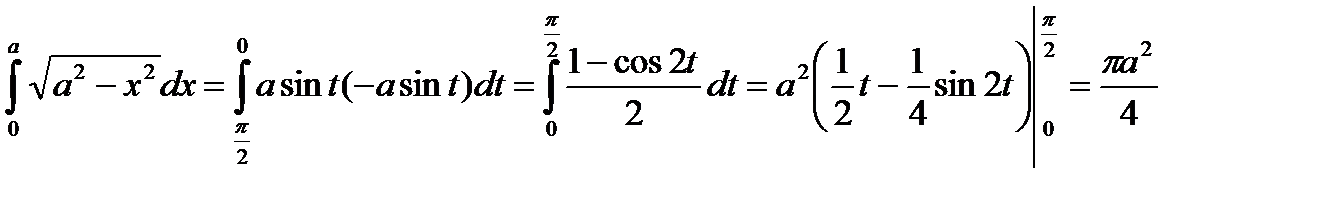

Лекция 7.

Тема: Интегрирование четных и нечетных функций. Несобственные интегралы.

7.1. Интегрирование четных и нечетных функций.

Пусть 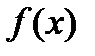- четная функция на отрезке 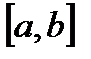, т.е. . Рассмотрим интеграл

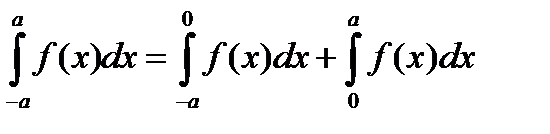
В интеграле 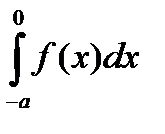сделаем замену переменной .

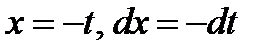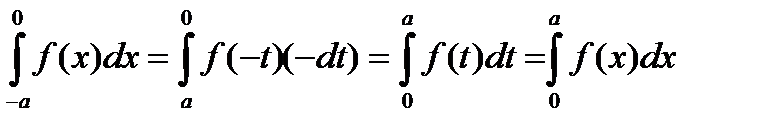
В результате получим

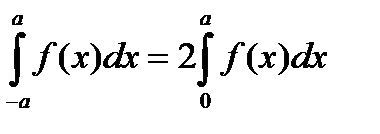
Пусть 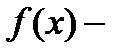нечетная функция на отрезке 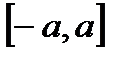, т.е. .

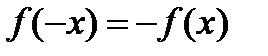Как и в предыдущем случае в интеграле 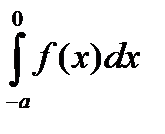сделаем замену 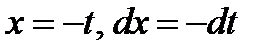. В результате получим: .

.

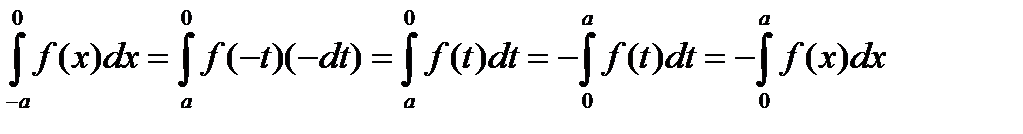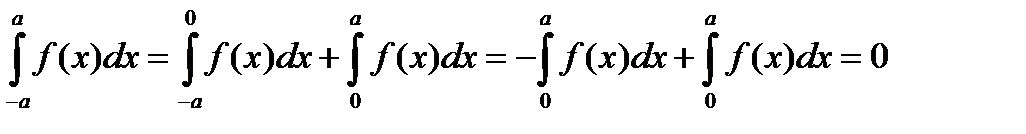7.2. Несобственные интегралы.

До сих пор мы рассматривали интегралы 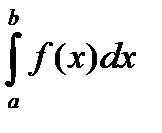, для которых отрезок 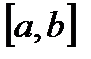конечен и функция 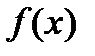ограничена на отрезке 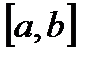. При этом .

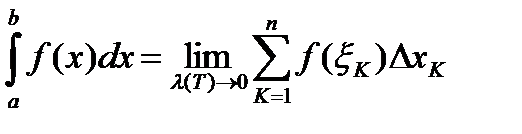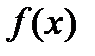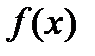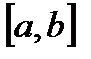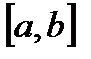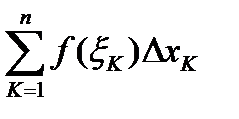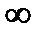На практике часто встречаются случаи, когда задана на бесконечном промежутке и непрерывна на нем либо задана на конечном отрезке , но неограниченна на нем. Если промежуток бесконечен, то при любом разбиении его на конечное число частей один из промежутков будет бесконечным, сумма равна , а 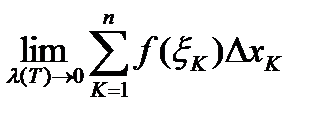не существует. Если же 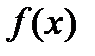определена на конечном отрезке 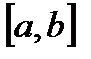, но неограниченна, то всегда существует отрезок разбиения 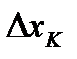, на котором 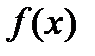неограниченна и на этом отрезке можно выбрать точку 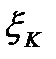так, что 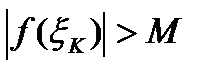, где М наперед заданное число и в этом случае 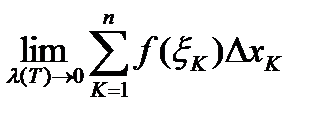не существует.

Если 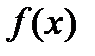задана на бесконечном промежутке и непрерывна на нем либо 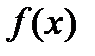задана на конечном промежутке и неограниченна на нем, то интегралы от таких функций определяются с помощью предельного перехода и эти интегралы называются несобственными.

7.2.1. Несобственные интегралы от непрерывных функций по бесконечному промежутку.

Пусть 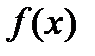задана и непрерывна на промежутке .

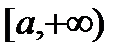Рассмотрим интеграл 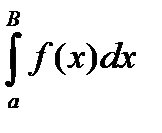, этот интеграл существует 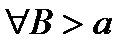, т.к. 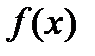непрерывна на отрезке .

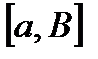Положим по определению

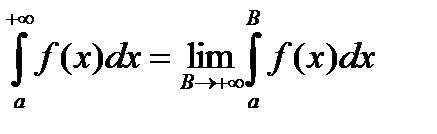. (1)

Интеграл 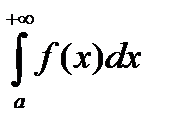называется несобственным интегралом. Если предел в равенстве (1) существует, то говорят, что несобственный интеграл сходится. Если предел в равенстве (1) не существует, то говорят, что несобственный интеграл расходится.

Пусть теперь функция 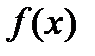задана и непрерывна на промежутке .

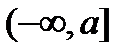Несобственный интеграл 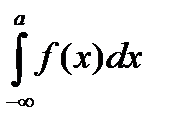определяется аналогично:

Далее, пусть функция 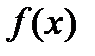задана и непрерывна на всей числовой оси .

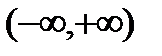Несобственный интеграл 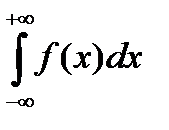определяется следующим образом:

,

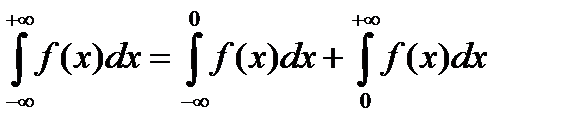при условии, что оба интеграла справа сходятся.

Заметим, что вместо 0 можно взять любое конечное число а и при этом сходимость несобственного интеграла 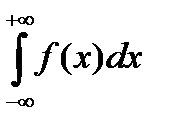и его значение не изменится.