Вычисление двойного нтеграла в декартовых координатах.

Вычисление объёмов тел площадей плоских фигур с помощью двойного интеграла.

Вычисление объемов с помощью двойного интегралаС помощью двойного интеграла, если воспользоваться его геометрической трактовкой, можно вычислить объем цилиндроида; формула для вычисления объема цилиндроида имеет вид:

где функция задает поверхность, ограничивающую цилиндроид сверху (Рис. 9)Более общая формула для вычисления объема тела с помощью двойного интеграла имеет вид: Она получается как разность объемов двух цилиндроидов (Рис. 10).Объемы других тел вычисляются двойным интегралом только в случаях, когда эти объемы представляются как сумма или разность объемов цилиндроидов.Напомним, что цилиндроидом называется геометрическое тело, которое в координатной системе XOYZ ограничено снизу областью , сверху – частью некоторой поверхности , сбоку – цилиндрической поверхностью с образующими, параллельными оси OZ.

Вычисление площади фигуры с помощью двойного интеграла.
Двойной интеграл применяется для вычисления площади плоской фигуры. f(x;y)=1 с высотой H=1. Объем такого цилиндра равен S обл. D.

В полярных координатах эта формула будет иметь вид:

Двойной интеграл легко вычисляется, если область D является прямоугольником. В этом случае двойной интеграл будет вычисляться через двукратный интеграл (повторный).
- двукратный интеграл, где интеграл f(x;y)dy - внутренний интеграл, а интеграл dx - внешний интеграл. Пределы интегрирования внешнего интеграла всегда должны быть числами. Пределы интегрирования внутреннего интеграла могут представлять либо числа, либо функцию.
Подынтегральная функция f(x;y) может разделяться на 2 переменных x и y в том случае, если представляет собой произведение или частное x и y. Если же функция представляет собой сумму или разность двух переменных x и y, то ее полностью записывают во внутренний интеграл и разделить ее нельзя.

6. Вычисление площадей поверхностей с помощью двойного интеграла.

Вычисление площади плоской фигурыПлощадь плоской фигуры, ограниченной областью D, находится по формуле . (105)Если область определена в прямоугольной системе координат неравенством , то из (105) имеем . (106)Если область D определена в полярных координатах неравенством , , то . (107)

Вычисление площади пространственных поверхностейЕсли гладкая однозначная поверхность задана уравнением z = f (x,y),то площадь этой поверхности выражается формулой , (108)где D есть проекция данной поверхности на плоскость хОу.Если поверхность задана уравнением x = f (y, z),то для вычисления площади имеем аналогичную формулу . (109)Однако здесь D есть проекция поверхности на плоскость yOz.Аналогично, если поверхность задана уравнением y = f (x,z), , (110)где D – проекция поверхности на плоскость xOz.

Свойства

1) 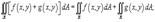2)

3) 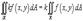, где k –

константа;

4)Если 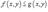в области R,то ;

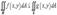5)Если 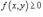в области R и 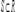, то ;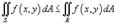

6)Если 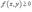на R и области R и S являются непересекающимися , то .
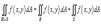Здесь означает объединение этих двух областей.

9. Вычисление тройного интеграла в декартовых координатах.Пусть функция 3-х переменных u = f (x, y, z) задана и непрерывна в замкнутой области V 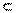xOyz. Тройной интеграл от этой функции по области V имеет вид: 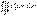, где 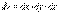.Если область V – правильная в направлении оси Oz (рис. 5), то ее можно задать системой неравенств: 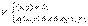где z = z1 (x, y) и z = z2 (x, y) – это уравнения поверхностей, ограничивающих область (тело) V соответственно снизу и сверху (рис. 5). Если область D можно задать системой неравенств 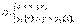то 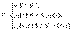В этом случае тройной интеграл от функции u = f (x, y, z) по области V можно вычислить при помощи трехкратного повторного интеграла: 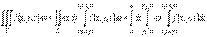.Здесь каждый внутренний интеграл вычисляется по «своей» переменной интегрирования в предположении, что переменные интегрирования внешних интегралов остаются постоянными.Существует всего 6 вариантов сведения тройного интеграла к трехкратному в декартовых координатах (в зависимости от выбранного порядка интегрирования).Вычисление тройного интеграла в цилиндрических координатахЦилиндрические координаты точки М в пространстве – это ее полярные координаты на плоскости xOy и координата z, т.е. 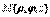.Преобразование тройного интеграла по области V к цилиндрическим координатам осуществляется при помощи формул 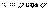, , 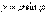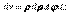: 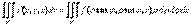.Если область V задана системой неравенств: 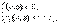причем 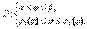то V: 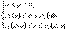Вычисление тройного интеграла по области V в цилиндрических координатах сводится к вычислению трехкратного интеграла в соответствии с записанной системой неравенств для области V: .

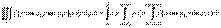Основные свойства КРИ-I

1. , т.е. криволинейный интеграл I рода не зависит от направления пути интегрирования.

2. , где .

3. .

4. , если путь интегрирования разбить на части и такие, что , и имеют единственную общую точку.

5. Если для точек кривой выполняется неравенство , то .

6. Если , то , где - длина кривой (геометрический смысл криволинейного интеграла первого рода).

7. (Теорема о среднем) Если функция непрерывная на кривой , то на этой кривой найдется точка , что .

Площадь плоской фигуры

Площадь плоской фигуры, расположенной в плоскости и ограниченной замкнутой линией , можно найти по формуле

,при этом кривая , делает обход против часовой стрелки.

Работа переменной силы

Переменная сила на криволинейном участке производит работу, которая находится по формуле

.

Основные свойства КРИ-II

1. При изменении направления пути интегрирования криволинейный интеграл II рода изменяет свой знак на противоположный, т.е.

.

2. Если кривая точкой разбита на две части и , то интеграл по всей кривой равен сумме интегралов по ее частям, т.е.

.

Если кривая интегрирования замкнута, криволинейный интеграл II рода обозначается . В этом случае через кривую проводится ориентированная поверхность и за положительное направление обхода по Lпринимается такое направление, при котором область поверхности, ограниченная кривойL, находится слева, если двигаться вдоль Lпо выбранной стороне указанной поверхности, т.е. за положительный обход контура Lпринимается обход против хода часовой стрелки.

Если плоскую область , ограниченную кривой , разбить на части, не имеющие общих внутренних точек и ограниченные замкнутыми кривыми и , то ,где направления обхода по контурам , и - всюду либо положительные, либо отрицательные.

Приложения КРИ(1-2)

Длина кривой

Длина кривой , плоской или пространственной линии, вычисляется по следующей формуле .

Масса кривой

Если - плотность материальной кривой (провод, цепь, трос, …), то ее масса вычисляется по формуле:

.

Координаты центра масс

Координаты центра масс материальной дуги , имеющей плотность , определяются по формулам:

; ; .

Моменты инерции

Моменты инерции относительно начала координат , осей координат и , и координатных плоскостей и материальной дуги , имеющей плотность , определяются по формулам:

;

, ,

, , .

Свойства ПОВИ-2

1. Поверхностный интеграл II рода изменяет знак при перемене стороны поверхности.

2. Постоянный множитель можно вынести за знак поверхностного интеграла.

3. Поверхностный интеграл от суммы функций равен сумме соответствующих интегралов от слагаемых.

4. Поверхностный интеграл II рода по всей поверхности равен сумме интегралов по ее частям и (аддитивное свойство), если и пересекаются лишь по границе, их разделяющей.

5. Если , и - цилиндрические поверхности с образующими, параллельными соответственно осям , то

.

Формула Стокса

Рассмотрим в пространстве кусок двухсторонней кусочно-гладкой поверхности , край которой образуется кусочно-гладкой кривой . Выберем положительную сторону поверхности (из конца единичного вектора нормали обход границы представляется против часовой стрелки). Для циркуляции векторного поля вдоль контура границы имеет место формула Стокса: , где - компоненты векторного поля, - направляющие косинусы вектора нормали.

Вариант №2 .

(4.14)

Эту же формулу Стокса можно записать и векторной форме:

. (4.15)

Формула (4.15) означает следующее: циркуляция векторного поля вдоль замкнутого контура равна потоку ротора этого поля через любую гладкую поверхность , краем которой является контур . Направление обхода по контуру и сторона поверхности одновременно или положительные, или отрицательные.

Скалярное поле

Если в области 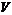задана скалярная функция точки , то говорят, что в этой области задано скалярное поле.Если - область трехмерного пространства, то скалярное поле можно рассматривать как функцию трех переменных - координат точки , т.е.

.

Если скалярная функция зависит только от двух переменных 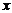и , то соответствующее скалярное поле называют плоским.

В дальнейшем будем предполагать, что скалярная функция - определяющая скалярное поле, непрерывна вместе со своими частными производными.Для наглядного представления скалярного поля используют поверхности и линии уровня.

Поверхностью уровня скалярного поля называется геометрическое место точек, в которых функция принимает постоянное значение, т.е.

. В случае плоского поля равенство представляет собой уравнение линии уровня поля – линии на плоскости , в точках которой функция сохраняет постоянное значение.

Пусть скалярное поле задано функцией , где значения

откладываются по оси . Линиями уровня на плоскости будут проекции линий, которые получаются в пересечении поверхности с плоскостями (см. рисунок).

Линии уровня применяются в математике при исследовании поверхностей методом сечений.

Свойства Grad :

1) Производная в данной точке по направлению вектора имеет наибольшее значение, если направление вектора совпадает с направлением градиента, когда , т.е. при ; это наибольшее значение производной равно .Таким образом, направление градиента есть направление наискорейшего возрастания функции. В противоположном направлении функция будет быстрее всего убывать. - наибольшая скорость изменения функции в точке .

2) Производная по направлению вектора, перпендикулярного к вектору , равна нулю.

3) Градиент функции в каждой точке направлен по нормали к поверхности уровня скалярного поля, проходящего через эту точку.

4) .

5) , где .

6) и др.

Градиент

В каждой точке области 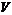, в которой задана скалярная функция , определим вектор, проекциями которого на оси координат являются значения частных производных в выбранной точке . Назовем этот вектор градиентом функции и обозначим его символами или (набла-оператор, записываемый в виде «вектора» с компонентами ).

Градиентом функции в точке называется вектор, проекции которого служат значения частных производных этой функции, т.е.

. (4.3)

Подчеркнем, что проекции градиента зависят от выбора точки и изменяются с изменением координат этой точки. Таким образом, каждой точке скалярного поля, определяемого функцией , соответствует определенный вектор – градиент этой функции. Отметим, что градиент линейной функции есть постоянный вектор .

Используя определение градиента, формуле для производной по направлению можно придать следующий вид:

,которая читается так: производная функции по данному направлению равна скалярному произведению градиента функции на единичный вектор этого направления ( ).Учитывая то, что скалярное произведение равно модулю одного вектора умноженному на проекцию другого вектора на направление первого, то можно еще сказать, что: производная функции по данному направлению равна проекции градиента функции на направление дифференцирования, т.е.

,

где j - угол между и направлением .

Интегральный признак Коши.

Вариант 2

Сходимость или расходимость числовых рядов с положительными членами часто устанавливается путем сравнения его с другим («эталонным») рядом, о котором известно, сходится он или нет. В основе такого сравнения лежат следующие теоремы.

Теорема 5.3. Пусть даны два ряда с положительными членами:

и

Если для всех 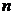выполняется неравенство , то

1) из сходимости ряда (5.9) следует сходимость ряда (5.8);

2) из расходимости ряда (5.8) следует расходимость ряда (5.9).

Надо отметить, что теорема 5.3 справедлива и в том случае, когда неравенство выполняется не для всех членов рядов (5.8) и (5.9), а начиная с некоторого номера . Это вытекает из свойства 3 числовых рядов.

Признак Даламбера.

В отличие от признаков сравнения, где все зависит от догадки и запаса известных сходящихся и расходящихся рядов, признак Даламбера (1717 – 1783, французский математик) позволяет часто решать вопрос о сходимости ряда, проделав лишь некоторые операции над самими рядами.

Теорема 5.5 (признак Даламбера). Пусть дан ряд (5.1) с положительными членами и существует конечный или бесконечный предел

.

Тогда:

1) при ряд сходится;

2) при ряд расходится.

При признак Даламбера не дает ответа на вопрос о сходимости или расходимости ряда. В этом случае сходимость ряда исследуется с помощью других признаков.

Признак Даламбера целесообразно применять, когда общий член ряда содержит выражения вида или .

Радикальный признак Коши

Иногда удобно пользоваться радикальным признаком Коши для исследования сходимости числового ряда с положительными членами. Этот признак во многом схож с признаком Даламбера.Теорема 5.6 (радикальный признак Коши). Пусть дан ряд (5.1) с положительными членами и существует конечный или бесконечный предел

.

Тогда:

1) при ряд сходится;

2) при ряд расходится.

При радикальный признак Коши не дает ответа на вопрос о сходимости или расходимости ряда. В этом случае сходимость ряда исследуется с помощью других признаков.

Свойства степенных рядов.

Сформулируем без доказательства основные свойства степенных рядов.

1)Сумма степенного ряда (7.3) является непрерывной функцией в интервале сходимости .

2)Степенные ряды и , имеющие радиусы сходимости соответственно и , можно почленно складывать, вычитать и умножать. Радиус сходимости произведения, суммы и разности рядов не меньше, чем меньшее из числе и .

3)Степенной ряд внутри интервала сходимости можно почленно дифференцировать. Для ряда

при

. (7.6)

4)Степенной ряд можно почленно интегрировать на каждом отрезке, расположенном внутри интервала сходимости. Для ряда (7.3) при выполняется равенство

Ряды (7.6) и (7.7) имеют тот же радиус сходимости, что и исходный степенной ряд. Перечисленные свойства остаются справедливыми и для степенных рядов вида .

Ряды Тейлора и Маклорена.

Для приложений важно уметь данную функцию представлять в виде суммы степенного ряда.Для любой функции , определенной в окрестности точки и имеющей в ней производные до -го порядка включительно, справедлива формула Тейлора:

,

где , - остаточный член в форме Лагранжа. Причем число можно записать в виде , где .

Формулу (7.8) можно записать в виде

,

где - многочлен Тейлора.

Если функция имеет производные любых порядков (т.е. бесконечно дифференцируема) в окрестности точки и остаточный член стремится к нулю при ( ), то из формулы Тейлора получается разложение функции по степени , называемое рядом Тейлора:

Если в ряде Тейлора положить , то получим разложение функции по степеням в так называемый ряд Маклорена:

Отметим, что ряд Тейлора можно формально построить для любой бесконечно дифференцируемой функции (это необходимое условие) в окрестности точки . Но отсюда еще не следует, что он будет сходиться к данной функции ;он может оказаться расходящимся или сходится, но не к функции .

В следующей теореме (которую примем без доказательства) сформулировано необходимое и достаточное условие сходимости ряда Тейлора к функции .

Теорема Для того чтобы ряд Тейлора (7.9) функции сходился к функции в точке , необходимо и достаточно, чтобы в этой точке остаточный член формулы Тейлора (7.8) стремился к нулю при 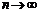, т.е. чтобы .

Для разложения функции в ряд Маклорена (7.10) нужно:

1. найти производные ;

2. вычислить значения производных в точке ;

3. выписать ряд (7.10) для заданной функции и найти его интервал сходимости;

4. найти интервал , в котором остаточный член ряда Маклорена при 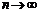. Если такой интервал существует, то в нем функция и сумма ряда Маклорена совпадают.

Вычисление двойного нтеграла в декартовых координатах.

Покажем, что вычисление двойного интеграла сводится к последовательному вычислению двух определенных интегралов.Пусть требуется вычислить двойной интеграл где функция ƒ(х;у)>=0 непрерывна в области D. Тогда, как это было показано в п. 7.2, двойной интеграл выражает объем цилиндрического тела, ограниченного сверху поверхностью z=ƒ(х;у). Найдем этот объем, используя метод параллельных сечений. Ранее (см. Часть 1, (41.6)) было показано, что где S(x) - площадь сечения плоскостью, перпендикулярной оси Ох, a x=a,x=b - уравнения плоскостей, ограничивающих данное тело.Положим сначала, что область D представляет собой криволинейную трапецию, ограниченную прямыми х=а и х=b и кривыми у=₁(x) и у=₂(х), причем функции ₁(x) и ₂(х) непрерывны и таковы, что ₁(x) ≤ ₂(х) для всех х є [а;b] (см. рис. 7). Такая область называется правильной в направлении оси Оу: любая прямая, параллельная оси Оу, пересекает границу области не более чем в двух точках.Построим сечение цилиндрического тела плоскостью, перпендикулярной оси Ох: х =const, где х є [а; b].В сечении получим криволинейную трапецию ABCD, ограниченную линиями z=ƒ(х;у), где х=const, z=0, у=₁(x) и у=₂(х) (см. рис. 8). Площадь S(х) этой трапеции находим с помощью определенного интеграла Теперь, согласно методу параллельных сечений, искомый объем цилиндрического тела может быть найден

так:

С другой стороны, в п. 7.2 было доказано, что объем цилиндрического тела определяется как двойной интеграл от функции ƒ(х;у) >=0 по области D. Следовательно, Это равенство обычно записывается в виде Формула (7.7) представляет собой способ вычисления двойного интеграла в декартовых координатах. Правую часть формулы (7.7) называют двукратным (или повторным) интегралом от функции ƒ(х; у) по области D.При этом называется внутренним интегралом.Для вычисления двукратного интеграла сначала берем внутренний интеграл, считая х постоянным, затем берем внешний интеграл, т. е. результат первого интегрирования интегрируем по х в пределах от а до b.Если же область D ограничена прямыми y=c и y=d(c<d), кривыми x=Ψ₁(у)и х=Ψ₂(у)> причем Ψ₁(у)≤Ψ₂(у) для всех у є [с;d], т. е. область D - правильная в направлении оси Ох, то, рассекая тело плоскостью у=const, аналогично получим: Здесь, при вычислении внутреннего интеграла, считаем у постоянным.

3.Двойной интеграл в полярных координатахДля упрощения вычисления двойного интеграла часто применяют метод подстановки (как это делалось и при вычислении определенного интеграла), т. е. вводят новые переменные под знаком двойного интеграла.Определим преобразование независимых переменных х и у (замену переменных) как Если функции (7.9) имеют в некоторой области D* плоскости Ouv непрерывные частные производные первого порядка и отличный от нуля определитель

а функция ƒ(х;у) непрерывна в области D, то справедлива формула замены переменных в двойном интеграле:

Функциональный определитель (7.10) называется определителем Якоби или якобианом (Г.Якоби - немецкий математик). Доказательство формулы (7.11) не приводим.Рассмотрим частный случай замены переменных, часто используемый при вычислении двойного интеграла, а именно замену декартовых координат х и у полярными координатами r и .В качестве u и υ возьмем полярные координаты r и . Они связаны с декартовыми координатами формулами х=rcos , у=r sin  (см. Часть 1, п. 9.1).Правые части в этих равенствах - непрерывно дифференцируемые функции. Якобиан преобразования определяется из (7.10) как