Плоская задача теории упругости в декартовых координатах

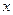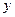Решение трехмерных задач теории упругости вызывает значительные математические трудности. Это обстоятельство заставляет строить более простые модели деформируемого тела, имеющие большое значение для практических приложений. К числу их относятся плоские задачи теории упругости, в которых напряженно-деформированное состояние тела зависит только от двух координат (скажем и ). Такие двумерные состояния реализуются в теле при вполне определенных условиях, и в этом параграфе мы подробно изучим их для двух случаев, известных под названием плоское напряженное состояние и плоская деформация (плоское деформированное состояние).

Но прежде сделаем некоторые замечания, касающиеся, вообще говоря, всех плоских задач теории упругости и связанные с ограничениями, которые следует наложить на внешнюю нагрузку и геометрию тела с целью реализации в нем двумерного напряженно-деформированного состояния.

Предположим, что напряжения в теле зависят от двух координат 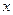и 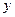. Тогда уравнения равновесия (1.11) примут вид

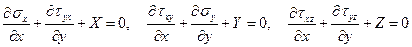(1.47)

Отсюда заключаем, что объемные силы 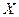, , 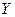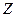должны зависеть только от 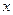и 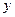. Аналогичный вывод можно сделать и в отношении поверхностных сил 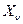, , 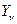, 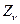если обратиться к условиям на поверхности (1.9) и принять, что направляющие косинусы 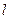, , 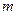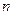внешней нормали 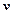к границе тела также не зависят от 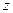. Последнее утверждение равносильно тому, что границей тела с двумерным напряженным состоянием являются цилиндрическая поверхность с образующей, параллельной оси 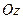, и две плоскости, параллельные координатной плоскости .

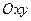Таким образом, для реализации в теле двумерного напряженного состояния (а в силу закона Гука и деформированного) достаточно потребовать, чтобы все внешние нагрузки зависели только от двух соответствующих координат, а граница тела слагалась из указанных выше цилиндрической поверхности и плоскостей.

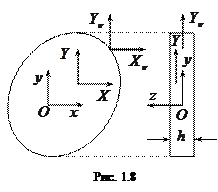1.7.1. Плоское напряженное состояние. Рассмотрим упругое тело, объем которого заключен между цилиндрической поверхностью с образующей, параллельной оси , и двумя плоскостями, параллельными координатной плоскости и удаленными друг от друга на расстоянии . Величину 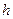будем считать малой по сравнению с минимальным размером тела в плоскости (см.рис.1.8). Такие тела принято называть пластинами.

Предположим, что на пластину действуют независящие от координаты z внешние силы: объемные , ( 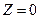) и поверхностные 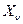, , 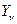( 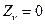), приложенные к цилиндрической поверхности. Граничные плоскости 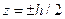будем считать свободными от нагрузки.

На границе пластины условия на поверхности (1.9) принимают вид:

для цилиндрической поверхности —

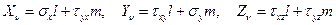(1.48)

для плоскостей 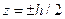соответственно —

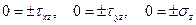(1.49)

Здесь 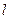, 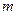— не зависящие от 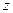направляющие косинусы внешней нормали к цилиндрической поверхности.

Напряжения 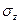, , 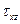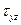определены по 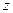на малом отрезке 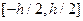и на концах его обращаются в нуль (см.(1.49)). Непрерывность этих напряжений по 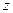позволяет сделать заключение, что их значения для любой внутренней точки тела будут близки к нулю. Используя это обстоятельство, примем допущение: во всех точках пластины равенство

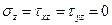(1.50)

Выполняется тождественно.

Из первых двух уравнений (1.48) следует, что напряжения 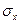, , 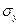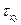не зависят от 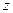, и третье уравнение (1.48) в силу (1.50) обращается в тождество. Полученное нами двумерное состояние тела называют плоским напряженным состоянием. В соответствии с вышеизложенным оно реализуется в тонких пластинах при действии на них независящих от 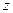объемных 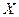, 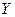сил и поверхностных сил 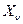, , 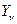приложенных к цилиндрической части границы, и при соблюдении равенств (1.50), составляющих для плоского напряженного состояния содержание определяющей гипотезы. Используя все эти условия, получим полную систему уравнений плоского напряженного состояния.

Согласно гипотезе (1.50) пространственные уравнения равновесия (1.11) и условия на поверхности (1.9) примут вид

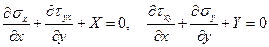(1.51)

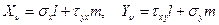(1.52)

причем уравнения (1.52) ставятся на цилиндрической части границы тела.

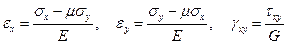(1.53)

и далее

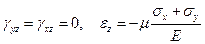(1.54)

Отсюда следует, что не обращающиеся в нуль деформации не зависят от 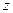, а, следовательно, от этой переменной не должны зависеть и упругие смещения — смещения, отличные от смещений пластины как жесткого целого. Последнее уравнение (1.54) показывает, что деформация удлинения 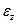обусловлена эффектом Пуассона и однозначно определяется основными напряжениям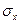и и .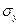

Обратная форма уравнений (1.53), очевидно, имеет вид

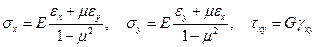. (1.55)

Существенными для плоского напряженного состояния деформационными соотношениями Коши являются

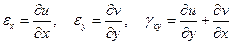. (1.56)

Нетрудно убедиться в том, что в силу независимости этих деформаций от координаты и уравнений (1.54), из шести уравнений сплошности (3.30) останется только первое

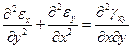, (1.57)

а остальные обращаются в тождества вида .

Таким образом, полную систему уравнений, определяющих математическую модель плоского напряженного состояния, образуют уравнения (1.51)-(1.53),(1.55)-(1.57).

1.7.2. Плоская деформация. Пусть теперь граница упругого тела представлена цилиндрической поверхность с образующей, параллельной оси 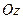, и двумя плоскостями, параллельными координатной плоскости 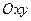, расстояние 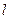между которыми намного превышает максимальный размер тела в плоскости 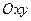(см.рис.7.2). Такие тела называются стержнями.

Будем считать, что действующие на тело внешние силы не зависят от координаты 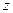и представлены объемными силами 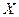, 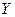и приложенными к цилиндрической границе поверхностными силами , .

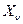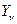В качестве определяющей гипотезы плоской деформации примем предположение о следующей зависимости перемещений точек тела

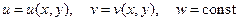(1.58)

Тогда из соотношений Коши сохраняют силу зависимости (1.56), в которых 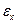, 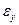и 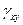— функции только 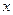, , 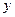а также следуют равенства

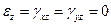(1.59)

С учетом этого убеждаемся, что, как и в плоском напряженном состоянии, остается единственное условие сплошности (1.57).

Обращаясь теперь к обобщенному закону Гука (1.32), (1.34), находим

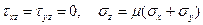(1.60)

и далее с учетом последнего соотношения (1.60)

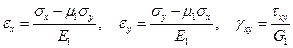(1.61)

Здесь введены обозначения

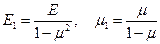(1.62)

и учтено тождество

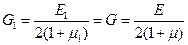(1.63)

Нетрудно показать, что статические уравнения плоской деформации в точности совпадают с уравнениями (1.51), (1.52). Таким образом, если за основные принять напряжения 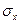, , 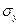, 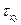то напряжение 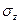(см. (1.60)) является вторичной величиной. Подобно 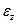в плоском напряженном состоянии оно обусловлено эффектом Пуассона и однозначно выражается через 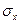и .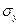

Итак, если исключить из рассмотрения соответствующие вторичные величины, то полные системы уравнений плоского напряженного состояния и плоской деформации совпадают с точностью до упругих постоянных. А это означает, что всякой задаче о плоском напряженном состоянии можно сопоставить соответствующую задачу о плоской деформации, решение которой сейчас же находится по решению первой задачи путем замены в нем упругих постоянных 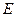, , 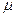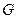на 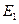, , 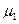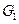соответственно. И наоборот.

Такая идентичность моделей плоского напряженного состояния и плоской деформации позволяет нам не разграничивать их при решении конкретных задач и проводить все построения применительно, скажем, к плоскому напряженному состоянию.

1.7.3. Метод напряжений в плоской задаче. Все сказанное выше (см. 5) о постановке и методах решения пространственных задач теории упругости можно дословно повторить и для случая плоской задачи с соответствующей редакцией на ее двумерность. Здесь мы рассмотрим подробно применение метода напряжений при решении плоской задачи теории упругости.

Примем за основные неизвестные напряжения 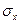, , 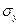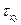. Эти три величины должны удовлетворять двум уравнениям равновесия (1.51)

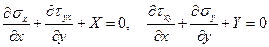
Следовательно, плоская задача — статически неопределима. Чтобы получить недостающее третье уравнение, подставим в уравнение сплошности (1.57) выражения (1.53). В результате найдем уравнение

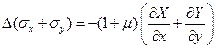(1.64)

носящее имя Морриса Леви

Здесь

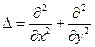(1.65)

— двумерный оператор Лапласа.

Система дифференциальных уравнений (1.61), (1.64) служит для определения искомых напряжений и при общих посылках может быть сведена к одному уравнению.

Ограничимся частным случаем, когда объемные силы 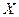, 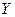равны нулю.

Тогда сводимая к одному уравнению система примет вид

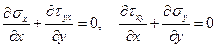(1.66)

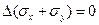
Первым двум уравнениям можно удовлетворить, полагая

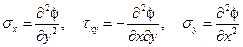(1.67)

Третье уравнение системы (1.66) с учетом формул (1.67) принимает вид

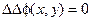(1.68)

или в развернутой записи

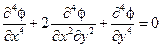(1.69)

Итак, плоская задача теории упругости применением метода напряжений свелась к интегрированию одного дифференциального уравнения (1.69) в частных производных относительно единственной функции 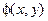. Эта функция определена формулами (1.67) и называется функцией напряжений или функцией Эри.Поскольку уравнение (1.69) имеет четвертый порядок, то 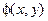должна принадлежать классу непрерывных функций, имеющих непрерывные частные производные до четвертого порядка включительно. Заметим, что в математической физике уравнения вида (1.69) называют бигармоническими, а решения их — бигармоническими функциями. Поэтому можно сказать, что функция напряжений — бигармоническая.

По своей природе уравнение (1.68) является уравнением совместности деформаций, сформулированным через функцию напряжений. По отношению к плоской краевой задаче метода напряжений оно играет роль разрешающего уравнения. Общее его решение должно быть подчинено соответствующим краевым условиям. При постановке статических граничных условий следует пользоваться уравнениями (1.52), легко представляемыми через функцию напряжений с помощью формул (1.67). Геометрические граничные условия ставятся обычным образом в виде ограничений, накладываемых на перемещения по закрепленной части границы тела.

После определения функции напряжений и самих напряжений деформации находятся из уравнений обобщенного закона Гука (1.53). Перемещения отыскиваются затем путем интегрирования соотношений Коши с последующим удовлетворением геометрических граничных условий.