Условия интегрируемости функции. Свойства определенного интеграла, его экономический смысл.

Случаи инт-ти функций: Если f (x)∈C([a;b]), то f (x)∈ R([a;b]) . Если функция y = f (x) определена и монотонна на отрезке [a;b], то она интегрируема на этом отрезке. Если функция y = f (x) ограничена на отрезке [a;b] и непрерывна во всех точках этого отрезка, кроме конечного числа точек ck (k =1;m) , в которых функция имеет разрыв I рода, то эта функция интегрируема на [a;b]. Если f (x)∈ R([a;b]) , то ф-ция y = f (x) ограничена на [a;b].

1.Определенный интеграл не зависит от выбора обозначения аргумента подынтегральной функции:

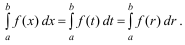
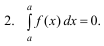
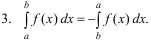
∫0*dx=0

Эк. смысл:

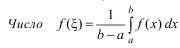
называется средним значением функции y = f (x) на отрезке [a;b], используется на практике при вычислении средней производительности труда, среднего значения издержек производства и т.д.

Формула Ньютона-Лейбница.

Если f(x)εC(|a;b|) и F(x) –какая-нибудь первообразная для y=f(x) на этом отрезке, то справедлива ф-ла Н. Лейбница:

∫f(x)dx=F(b)-F(a).

Теорема барроу:Если f(x)εC(|a;b|), то производная ф-ции сущ. в любой хε|а;b|, причем F’(x)=f(x)

Замена переменной и интегрирование по частям в определенном интеграле.

Пусть y=f(x) интегрируема на АВ, x=φ(t) дифф-ма на |α;β|, где φ(α)=а,φ(β)=b, тогда имеет место формула замены переменной:

∫f(x)dx=∫f(φ(t))*φ’(t)*dt; Интегр. по частям:

Пустьu=u(x), v=v(x) – две непрерывные дифф-ые ф-ции на АВ, тогда: ∫u(x)*d(v(x))=u(x)*v(x)|^b_a - ∫v(x)*d(u(x))

Приложения определенного интеграла (формулы для площади плоской фигуры и для длины дуги кривой).

Площадь плоской фигуры: площадь криволинейной трапеции, ограниченной графиком функции, заданной на отрезке [a;b] ( f (x) ≥ 0), двумя прямыми x = a и

x = b и отрезком [a;b] оси абсцисс, определяется формулой:

S=∫f(x)dx. Если фигура, площадь которой ищем лжит под и над осью Ох, то разбивамотрзокинтегр-я на части так, что на этих чстях ф-иясохр. знак(+,-), бреминтергал с «+» по тем частям, где ф-цияf(x)>и равно 0 и «-» - f(x)< и равна 0.

площадь плоской фигуры:S=∫(f₂(x) – f₁(x))dx

Длина дуги кривой: под длиной дуги понимается предел, к которому стремится длина ломаной линии, вписанной в эту дугу, когда число звеньев ломаной возрастает неограниченно, а длина наибольшего звена стремится к нулю. На отрезке [a;b] кривая задана непрерывной функцией и существует производная f ′(x). Тогда длина кри-

вой будет определяться формулой:

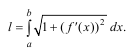
Несобственные интегралы первого рода, их геом. смысл. Признаки сравнения нес.интегралов 1-го рода.

Пусть дан интеграл, интервал от (а,b), где а и bм.б. конечными числами и равны а=-∞, b= +∞, тогда ∫f(x)dx, где f(x) –интегрируема на любом конечном отрезке. Если сущ. предел ,стремящ. к +∞∫f(x)dxи он конечен, то этот предел наз. несобственным инт. 1 рода.

Геом. смыслом несобственного интеграла 1 рода явл. в случае его сх-тисущ-я конечной площади, ограниченной площади справа, слева.

Несобственные интегралы второго рода, их геом. смысл. Признаки сравнения нес.интегралов 2 рода

этот интеграл сходится. В случае, если он = ∞ или не сущ., то несобств. инт. 2 рода - расдодящийся

Геом смысл в случае его сх-тиявл. сущ-е конечной площади у неограниченной сверху, снизу.