Независимость криволинейного интеграла от пути интегрирования.

Определение функции по ее полному дифференциалу.

Рассмотрим КРИ-2 по ориентированной дуге MN ,лежащей в некоторой области Д.Допустим, что значение интеграла не зависит от формы дуги,т.е

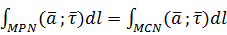,тогда поскольку

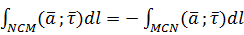,то

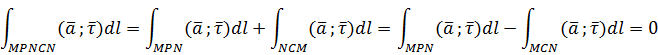
Можно показать, что справедливо и обратное утверждение и таким образом имеет место

Теорема 1 КРИ-2 по дуге из области Д не зависит от пути интегрирования ,тогда и только тогда,когда его значение по любому замкнутому контуру Д=0

В случае плоской кривой справедлива

ТЕОРЕМА2 если функции X(x;y) и Y(x;y) 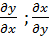непрерывны в области Д и на ее границе,то КРИ-2 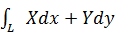не зависит от пути интегрирования тогда и только тогда, 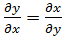внутри области Д и на ее границе.

При выполнении условия вычисления КРИ-2 может быть сведено к вычислению двух определенных интегралов.

Рассмотрим интеграл по линии MN

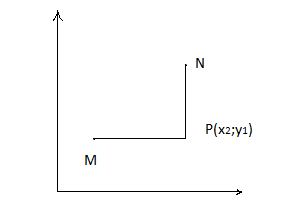
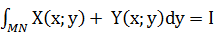
I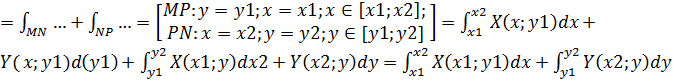

Определение функции по ее полному дифференциалу

Пусть в некоторой области Д для функции X(x;y) и Y(x;y) выполняется условие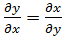

Как известно ,оно является необходимым и достаточным для того,чтобы выражение X(x;y) 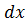+ Y(x;y) 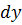было полным дифференциалом некоторой функции U(x;y)

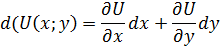
Тогда,если точки M и N принадлежат области Д,то

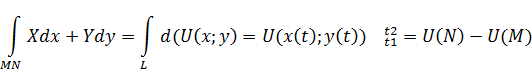
Если N(x;y),M(x₀;y₀),то U(N)=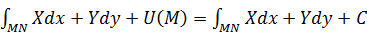

В качестве линии MN удобнее взять дугу MPN

Скалярные поля. Производная по направлению. Градиент.

(Стационарным) скалярным полем наз. область V 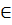Rⁿ, в каждой точке которой определена ф-я u(P)=u(x₁…x_n).

Скалярное поле можно представить графически с помощьюповерхностей уровня.

Поверхность уровня скалярного поля– множество точек, в каждой из которых u(P) сохраняет постоянное значение.

Для поля на двумерном пространстве аналогом поверхности уровня является линии уровня.

У-ние поверхности уровня на плоскости u(x;y)=c, в пространстве – u(x;y;z)=c.

Примерами скалярных полей являются: поле температуры T внутри тела, поле потенциалаφэлектрического заряда, поле плотности тела и т.д.

Производной ф-ииu(p)в точке P_o в направлении вектора 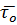наз-ся 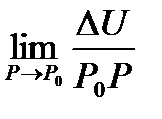. Обозначение 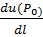, т.о. 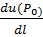= 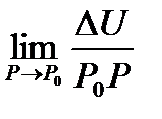. В пространств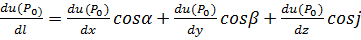е: , где 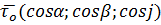. На плоскости: 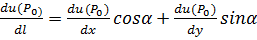, где .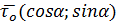

Градиентомскалярного поля u(P)в т.P_oназ-ся вектор, обознач. , .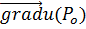

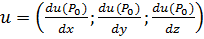Пусть направление l задается вектором 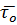с координатами 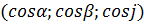, тогда проекция np_e .

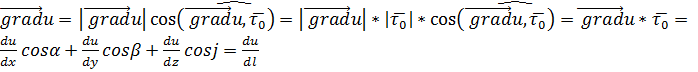Т.о. ф-я будет возрастать наиболее быстро в направлении 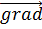. Следовательно, направление 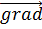явл-ся направлением наибыстрейшего возрастания скалярного поля данной точки. 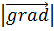равен наибольшей скорости возрастания.

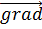направлен по нормали поверхности у-ня. У-ние нормали поверхности у-няu(x;y;z)=cв т. P_o(x_o;y_o;z_o) имеет вид:

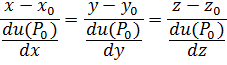
Если 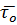направлен по касательной к поверхности уровня, то 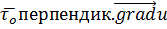, следовательно 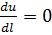. Можно сформулировать определение 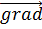, не зависящее от выбора сис-мы координат.

Градиентомскалярного поля наз. в-р, имеющий направление наибыстрейшего возрастания потенциала поля данной точки и модуль, равный максимальному значению производной потенциала.

Основные св-ва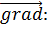

1)

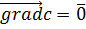
2)

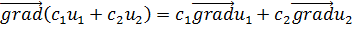
3)

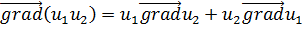
4)

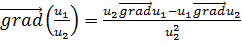
5)

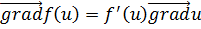
6)