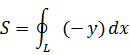Поверхностные интегралы 1 рода
Определение 1. Пусть Q- поверхность 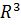 в пространстве, f(p)=f(x;y;z) непрерывная на Q на функция. Разобьем поверхность Q на n частей с площадями ∆
в пространстве, f(p)=f(x;y;z) непрерывная на Q на функция. Разобьем поверхность Q на n частей с площадями ∆ 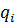 . На каждой из элементарных площадок выберем по точку
. На каждой из элементарных площадок выберем по точку 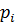 и составим интегральную сумму
и составим интегральную сумму 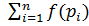 ∆
∆ 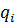 .
.
Пусть λ – max диаметр площадок, т.е. наибольшее расстояние между точками площадки
Если существует конечный предел при λ 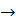 0
0 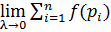 ∆
∆ 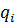 , который не зависит от способа разбиения площадок и выбора точек
, который не зависит от способа разбиения площадок и выбора точек 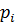 , то он называется ПИ-1 от f(p) по поверхности Q и обозначается
, то он называется ПИ-1 от f(p) по поверхности Q и обозначается 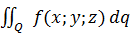
Теорема 1: Если функция f(p) непрерывна на замкнутой ограниченной поверхности Q , то ПИ-1 из опред. 1 существует.
Пусть поверхность Q гладкая(в каждой точке существует касательная плоскость) и правильная в направлении оси Oz(любая прямая || оси Oz пересекает Q не более чем в одной точке) тогда уравнение поверхности можно записать в явном виде z= 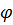 (x;y) , где
(x;y) , где  (x;y) – дифференцируемая на
(x;y) – дифференцируемая на  = D функция, а D – проекция Q на плоскость XOY α
= D функция, а D – проекция Q на плоскость XOY α
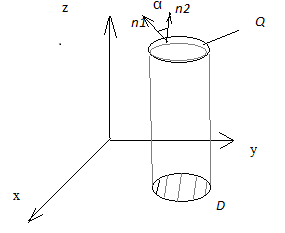
Пусть  - - единичныйвектор нормали к плоскости XOY(
- - единичныйвектор нормали к плоскости XOY( 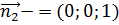 );
); 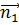 - вектор нормали к поверхности Q , т.к. уравнение Q можно записать z-
- вектор нормали к поверхности Q , т.к. уравнение Q можно записать z- 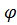 (x;y)=0,то
(x;y)=0,то 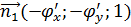
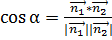 =
= 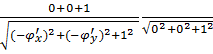 =
= 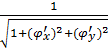
Так как площадь проекции равна произведению площади проектируемой поверхности на косинус угла между проектируемой поверхн. И плоскостью проекции, то ∂S=∂q*  =
= 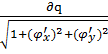
∂q= 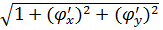 ∂S ;
∂S ; 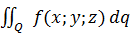 =
= 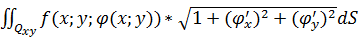 ,
, 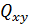 - проекция поверхности Q на XOY.
- проекция поверхности Q на XOY.
Замечание 1. Если поверхность Q –неправильная в направлении оси Oz, то её разбивают на правильные части и находят интеграл, как сумму интегралов по правильным частям.
Замечание 2. Можно проецировать поверхность на плоскости XOZ на YOZ.
КРИ 2-ого рода
Определение 1. Пусть дана ограниченная замкнутая линия L в пространстве OXYZ на плоскости OXY с ортонормированным базисом 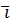 ,
, 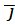 ,
, 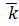 (
( 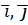 ). Если для каждой точки задан вектор
). Если для каждой точки задан вектор 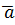 (P)=X(x;y;z)
(P)=X(x;y;z) 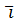 +Y(x;y;z)
+Y(x;y;z) 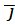 +Z(x;y;z)
+Z(x;y;z) 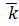 . Тогда говорят, что заданная функция
. Тогда говорят, что заданная функция 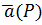 с областью опр. L.
с областью опр. L.
Определение 2. Линия называется ориентационной если указано направление её обхода: в каждой её точке задан ориентирующий вектор 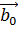 (p)=
(p)= 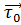 направленный по касательной к линии в сторону перемещения .
направленный по касательной к линии в сторону перемещения .
Определение 3. Пусть даны ориентированные линии L и векторная функция 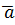 (p) заданная на L . Разобьем линию L на n элементарных линий с длинами ∆
(p) заданная на L . Разобьем линию L на n элементарных линий с длинами ∆ 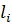 на каждой из элементарных линий выбранных по точке
на каждой из элементарных линий выбранных по точке 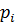 и составим интегральную сумму
и составим интегральную сумму 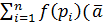
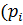 )*
)* 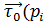 ) ∆
) ∆ 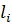
Если существует конечный предел 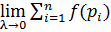 (
( 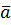
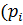 )*
)* 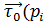 ) ∆
) ∆ 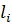
При стремлении max диаметра элементарных линий к 0, который не зависит от способа разбиения на элементарные линии и выбора точек 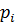 , то он называется КРИ-2 рода от функции
, то он называется КРИ-2 рода от функции 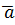 (p), по ориентированной линии L и обозначается
(p), по ориентированной линии L и обозначается 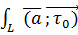 ∂l ;
∂l ;
Теорема 1. Если на ориентир. ограниченной замкнутой гладкой линии L координаты X(x;y;z), Y(x;y;z), Z(x;y;z) непрерывны, то КРИ-2 из опред 3 существует.
Основные свойства КРИ-2 аналогичны свойствам КРИ-1, например:
1) 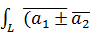 ,
, 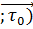 ∂l =
∂l = 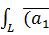
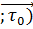 ∂l
∂l 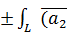
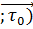 ∂l
∂l
2) 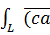
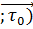 ∂l=
∂l= 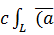
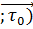 ∂l для
∂l для 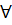 c
c 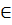 R
R
3) 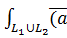
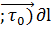 =
= 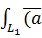
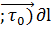 +
+ 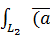
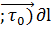
Где 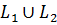 содержит не более одной точки
содержит не более одной точки
4) КРИ-2 обладает рядом специфических св-в
При изменении направления обхода РИ-2 меняет знак: 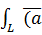
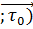 ∂l = -
∂l = - 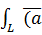
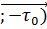 ∂l
∂l
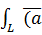
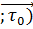 ∂l=
∂l= 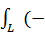
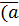
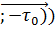 ∂l=
∂l= 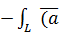
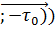 ∂l
∂l
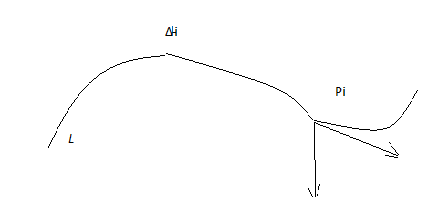
Рассмотрим механическое истолкование КРИ-2:
Пусть сила 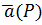 действует вдоль некоторой линии L меняясь как по величине, так и по направлению, т .е.:
действует вдоль некоторой линии L меняясь как по величине, так и по направлению, т .е.: 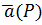 = (X(x;y;z); Y(x;y;z); Z(x;y;z)), тогда работа силы при перемещении по элементарной дуге ∆
= (X(x;y;z); Y(x;y;z); Z(x;y;z)), тогда работа силы при перемещении по элементарной дуге ∆ 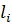 при условии что сила постоянна и равна
при условии что сила постоянна и равна 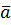
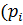 ), где
), где 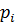 - некоторая точка дуги, равна ∆
- некоторая точка дуги, равна ∆ 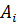 =|
=| 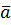
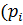 )|- ∆
)|- ∆ 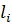 - cos(
- cos( 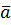
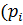 )
) 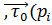 ))= (
))= ( 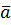
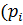 )
) 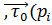 )) ∆
)) ∆ 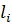
Суммарная работа силы А= 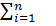 (
( 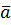
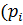 )
) 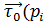 )) ∆
)) ∆ 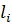
Переходя к пределу 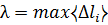 →0 получим А=
→0 получим А= 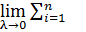 (
( 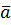
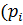 );
); 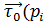 )) ∆
)) ∆ 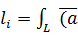
 ∂l
∂l
Т.е. с механической точки зрения КРИ-2 представляет собой работу переменной силы вдоль некоторой кривой.
Формула Грина
В случае замкнутого контура КРИ-2 обозначают  .Если направление обхода контура не указано, то предполагают, что обход конура совершают против часовой стрелки.
.Если направление обхода контура не указано, то предполагают, что обход конура совершают против часовой стрелки.
Пусть в плоскости ХОУ задана область Д ,ограниченная кривой L.
Предположим, что область Д правильная как в направлении оси ОХ, так и в направлении оси ОУ.
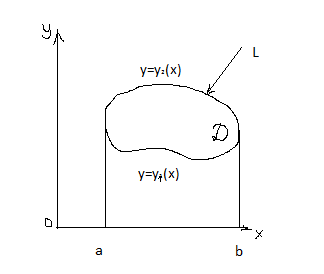 Д:x=a; x=b
Д:x=a; x=b
y=y1(x)
y=y2(x)
Пусть в области Д заданы функции X(x;y) и Y(x;y)-непрерывно дифференцируемые
Тогда:
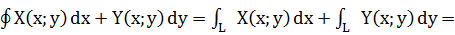 I1+I2
I1+I2
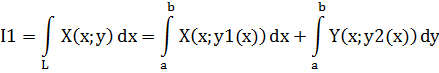
I2= 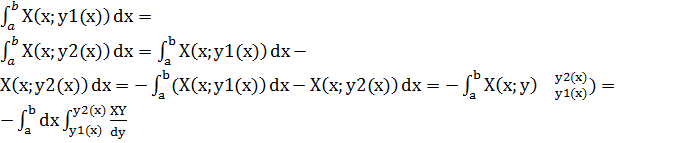
Аналогично
I2= 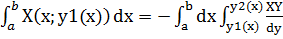
Таким образом
I1=- 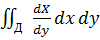
I2= 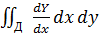
I=- 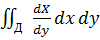 +
+ 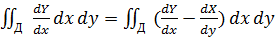
Получим формулу Грина
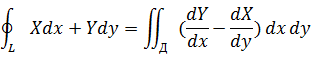
Замечание1 При изменении направления обхода,интеграл в правой части формулы меняет знак
Замечание 2 С помощью формулы Грина можно найти площадь плоской области
Если в скобках во втором интеграле получается 1,то 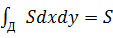
Так,если Y=x/2;X=-4/2,то
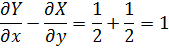
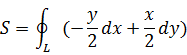
Аналогично при Y=x;X=0,
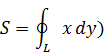
Если Y=0;X=-y