Числовые ряды. Необходимый признак сходимости. Простейшие свойства числовых рядов. Сходимость ряда, составленного из членов бесконечной геометрической прогрессии
Числовые ряды. Необходимый признак сходимости. Простейшие свойства числовых рядов. Сходимость ряда, составленного из членов бесконечной геометрической прогрессии
Пусть а(n)=а1,а2… - числовая последовательность. Выражение вида а1+а2+…+аn = ∑n=1∞an – называется числовым рядом, числа а1, а2 … - члены ряда. аn – общий член ряда.
Сумма конечного числа n первых членов ряда ∑k=1∞ak : a1 + a2 +…+ ak – называется n-ой частичной суммой ряда и обозначается Sn
Если последовательность (Sn )имеет конечный предел S, то это число называется суммой ряда, а ряд – сходящийся. Если предел бесконечен или не существует, то ряд – расходящийся.
Пример 3. Рассмотрим вопрос о сходимости ряда, составленного из членов бесконечной геометрической прогрессии.
b1+ b1q+ b1q2= 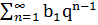 b1≠0
b1≠0
1) если модуль q=1
b1+b1+b1+…+b1 ; Sn=b1+…+b1=n*b1
n
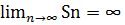 - Ряд расходиться
- Ряд расходиться
2) если модуль q= -1
ряд расходиться
3) если модуль q≠0
Sn= 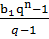
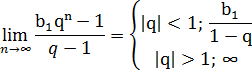
Ответ: ряд сходиться при 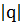 (Sn=
(Sn= 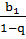 ) и расходиться при
) и расходиться при 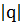 ≥1.
≥1.
Для числового ряда сумма ∑k=1∞ak выражение ak1+ak2+…=∑k=n+1∞a называется n-м остатком ряда. Для сходящегося числового ряда ∑k=1∞ak=∑k=1nak +∑k=n+1∞ak = Sn+rn.
Можно сказать, что последнее условие является не только необходимым , но и достаточным признаком сходимости ряда.
Теорема (необходимый признак сходимости ряда):
если ряд 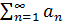 -сходиться, то
-сходиться, то 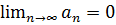 . Пусть
. Пусть 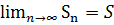 тогда
тогда 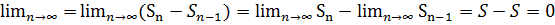
Теорема (достаточный признак расходимости):
если предел 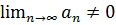 , то ряд
, то ряд 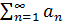 расходиться.
расходиться.
Простейшие свойства сходящихся числовых рядов:
1) Перестановка, отбрасывание или добавление конечного числа членов ряда не влияет на его сходимость.
2) Если ряды 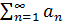 и
и 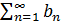 сходятся, то ряд
сходятся, то ряд 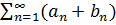 сходиться и его сумма
сходиться и его сумма 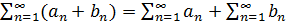 .
.
д-во:
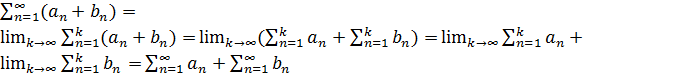
3) Если ряд 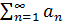 сходиться к числу S, то ряд
сходиться к числу S, то ряд 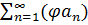 сходиться к числу
сходиться к числу 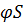 , где
, где 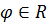 . Док-во аналогично св-ву 2.
. Док-во аналогично св-ву 2.
Операции суммирования рядов и умножения рядов на число называются линейными.
Знакопеременные ряды. Абсолютные и условные сходимости. Признак Лейбница.
Знакопеременный ряды – ряды, с членами разных знаков.
Пусть дан ряд 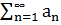 рассмотрим знакоположительный ряд
рассмотрим знакоположительный ряд 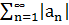
Теорема1. Если ряд 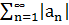 сходиться, то
сходиться, то 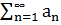 - сходиться.
- сходиться.
По свойствам сходимости рядов ряд 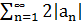 – сходиться, т.к. для любого nЄN, 0
– сходиться, т.к. для любого nЄN, 0 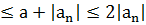 , то по признаку сравнения ряд
, то по признаку сравнения ряд 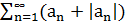 - сходиться.
- сходиться.
Значит ряд 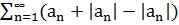 - сходиться.
- сходиться.
Т.1. даёт достаточный признак сходимости, который не является необходимым. В связи с этим сформулируем определение 1:
· если ряд 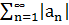 - сходиться, то говорят что ряд
- сходиться, то говорят что ряд 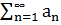 - сходиться абсолютно.
- сходиться абсолютно.
· если же ряд 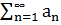 - сходиться, а ряд
- сходиться, а ряд 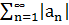 - расходиться, то говорят что
- расходиться, то говорят что 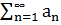 сходиться условно.
сходиться условно.
Знакочередующиеся ряды
Опр.2 Ими называют - ряды, члены которых поочередно меняют знак: a1-a2+a3-…
Где a1,a2,a3…. – одного знака. Удобно применять запись 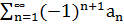
Признак Лейбница
Знакочередующийся ряд ( знаки членов которого строго чередуются) сходиться если:
1) Члены его убывают по абсолютному значению т.е. 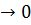 .
.
2) 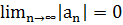
Замечание:
Признак Лейбница является достаточным, но не является необходимым.
Следствие 2.1
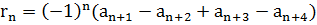 ;
; 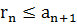 ; Остаток не превышает по модулю первый из отброшенных членов.
; Остаток не превышает по модулю первый из отброшенных членов.
Действительно остаток rn представляет собой ряд Лейбница 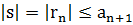
Функциональные ряды
Определение . 1
Пусть 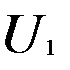 (X),
(X), 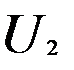 (x)… последовательность функций, определ-ых на некотороемножество X. Выражение вида
(x)… последовательность функций, определ-ых на некотороемножество X. Выражение вида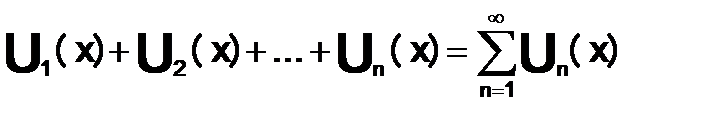 назыв. — функциональным рядом.
назыв. — функциональным рядом.
Каждому значению 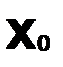
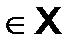 соответствует числовой ряд
соответствует числовой ряд 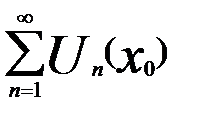 , если последний ряд сходится, то
, если последний ряд сходится, то 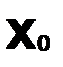 назыв.—точкой сходимости.
назыв.—точкой сходимости.
Множество всех точе сходимости функционального ряда назыв.— областью сходимости.
Конечная сумма 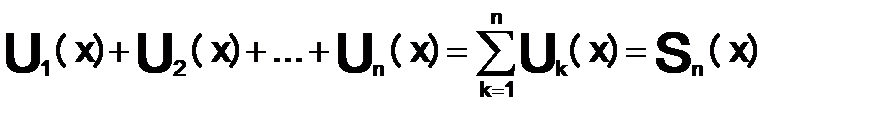 —n-ая частичная сумма ряда.А функция S(x)=
—n-ая частичная сумма ряда.А функция S(x)=  S(x) — суммой ряда.
S(x) — суммой ряда.
Область определения D(S(x)) — область сходимости.
Функция 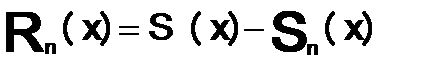 определенная на множестве D(S(x))назыв. — n-ый остаток ряда.Сходимость ряда в точке назыв. — поточечной.
определенная на множестве D(S(x))назыв. — n-ый остаток ряда.Сходимость ряда в точке назыв. — поточечной.
Функциональный ряд 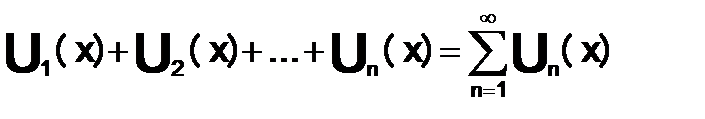 назыв. — абсолютно сходящимся на множестве
назыв. — абсолютно сходящимся на множестве 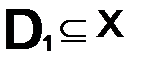 , если
, если 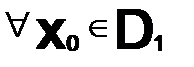 , ряд
, ряд 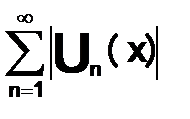 то такой ряд сходится.
то такой ряд сходится.
Опред. 2
Функциональный ряд 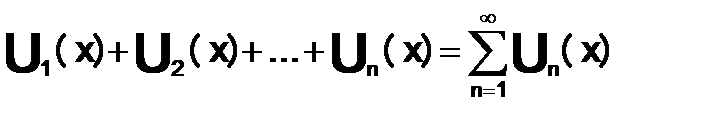 назыв. — равномерно сходящимся в области D функции S(x), если
назыв. — равномерно сходящимся в области D функции S(x), если 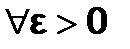
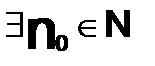 ,
, 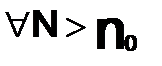 ,
, 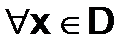
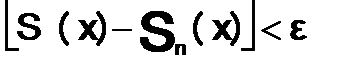 .
.
Отличие равномерной сходимости от поточечной в том, что номер 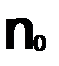 при равномерной сходимости зависит только от
при равномерной сходимости зависит только от 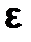 и не зависит от X.А при поточечной сходимости
и не зависит от X.А при поточечной сходимости 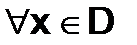 номер
номер 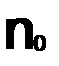 свой.
свой.
Поэтому из равномерной сходимости следует поточечная.
Дадим определение поточечной сходимости области ряда D.
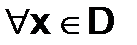 ,
, 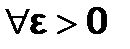
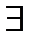
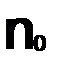
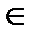 N(
N( 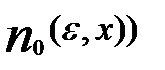
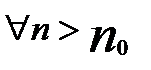
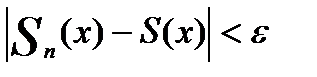
Следствие 2.1
В равномерно сходящемся ряде с непрерывно сходящимися членами возможен переход к пределу, т.е. 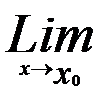
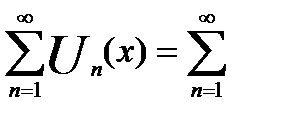
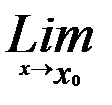
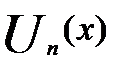
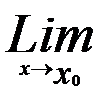
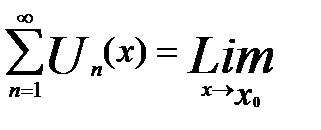 S(x)=S(
S(x)=S( 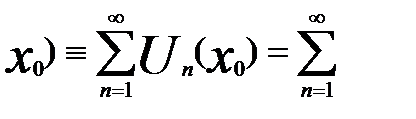
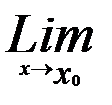
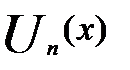
Определение 1
Ряд вида 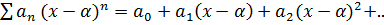 , где an, x
, где an, x 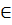 R, наз. степенным рядом по степеням
R, наз. степенным рядом по степеням 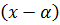 . При α=0 получаем ряд
. При α=0 получаем ряд 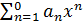 (*) по степеням x.
(*) по степеням x.
Т.к. 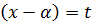 любой ряд можно свести к виду (*), то в дальнейшем будем рассматривать только такие ряды. При х=0 степенной ряд (*) сходится.
любой ряд можно свести к виду (*), то в дальнейшем будем рассматривать только такие ряды. При х=0 степенной ряд (*) сходится.
Теорема Абеля:
Если степенной ряд (*) сходится в т. X0≠0, то он сходится абсолютно в интервале (-|X0|;|X0|) и сходится равномерно на любом отрезке [-q;q], где 0<q< X0
Определение 2:
Радиус сходимости степенного рядо – это такое число R что ряд сход. в (-R;R) и расходится 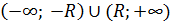
Если ряд сходится только в точке X=0, то R=0. Для нахождения радиуса сходимости используют признак Доламбера и Коши.
Теорема:
Если радиус сходимости степенного ряда ≠0, то его сумма не прерывна в (-R;R)
Теорема:
Операции почленного интегрирования и дефференцирования степ. ряда не меняют его радиус сходимости.
Ряды Тейлора и Маклорена
Пусть функция y=f(x) имеет в окрестности точки х0 производную любого порядка. Поставим в соответствие степенной ряд f(x) → f(х0) + f’(х0) (x- х0) + 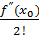 (x-x0)2 +
(x-x0)2 + 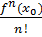 (x-x0)n+ … =
(x-x0)n+ … = 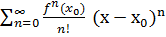 (*)
(*)
Ряд (*) называется рядом Тейлора в окрестности точки х0 функции f(x).
Если х0=0 то ряд Тейлора f(x) → f(0) + f’(0)x + 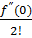 x2 +
x2 + 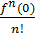 xn + … называется рядом Маклорена.
xn + … называется рядом Маклорена.
Радиус сходимости степенного ряда (*) может быть =0 или ≠0.
Причем в последнем случае сумма ряда может не совпадать с функцией f(x)
Важно знать S(x) = f(x).
Теорема 1 (Достаточный признак разложимости функций ряда Тейлора)
Если в некоторой окрестности (х0 –R; х0 +R) точки х0 все производные функции f(x) ограничены одной константой, то ряд сходится в функции f(x) в данной окрестности.
При условиях Т.1 ряд Тейлора сходится в функции для которой он составлен.
Свойства двойного интеграла
Поскольку конструкция двойного интеграла аналогична конструкции определенного интеграла, то они обладают аналогичными свойствами, поэтому докажем только одно.
1. Двойной интеграл от алгебраической суммы функции равна алгебраической сумме двойных интегралов данных функций.
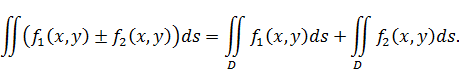
Док-во.
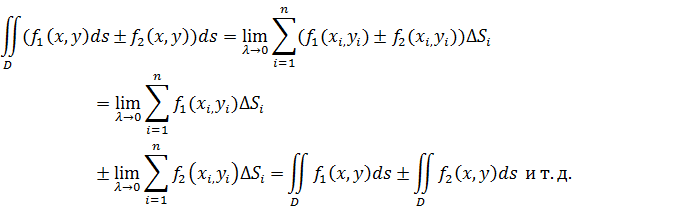
2. Постоянный множитель можно выносить за знак двойного интеграла
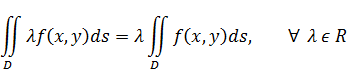
3. Если область интегрирования Dразбита на две области не имеющих внутренних точек D1 и D2, то двойной интеграл по области D равна
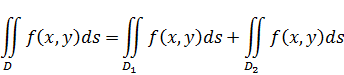
4. Если 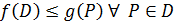
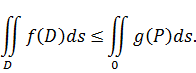
5. Для непрерывной замкнутой области Dфункцииf(x,y)
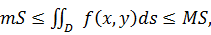 где m, M соответственно наименьшее и наибольшее значение функции в области D.S-площадь в области D.
где m, M соответственно наименьшее и наибольшее значение функции в области D.S-площадь в области D.
Приложение 3.1.
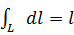 --длина L
--длина L
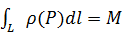 -- масса точки L
-- масса точки L
КРИ 2-ого рода
Определение 1. Пусть дана ограниченная замкнутая линия L в пространстве OXYZ на плоскости OXY с ортонормированным базисом 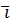 ,
, 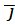 ,
, 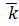 (
( 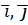 ). Если для каждой точки задан вектор
). Если для каждой точки задан вектор 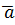 (P)=X(x;y;z)
(P)=X(x;y;z) 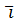 +Y(x;y;z)
+Y(x;y;z) 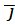 +Z(x;y;z)
+Z(x;y;z) 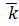 . Тогда говорят, что заданная функция
. Тогда говорят, что заданная функция 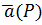 с областью опр. L.
с областью опр. L.
Определение 2. Линия называется ориентационной если указано направление её обхода: в каждой её точке задан ориентирующий вектор 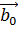 (p)=
(p)= 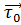 направленный по касательной к линии в сторону перемещения .
направленный по касательной к линии в сторону перемещения .
Определение 3. Пусть даны ориентированные линии L и векторная функция 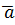 (p) заданная на L . Разобьем линию L на n элементарных линий с длинами ∆
(p) заданная на L . Разобьем линию L на n элементарных линий с длинами ∆ 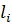 на каждой из элементарных линий выбранных по точке
на каждой из элементарных линий выбранных по точке 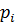 и составим интегральную сумму
и составим интегральную сумму 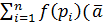
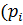 )*
)* 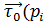 ) ∆
) ∆ 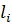
Если существует конечный предел 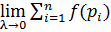 (
( 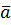
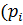 )*
)* 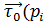 ) ∆
) ∆ 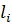
При стремлении max диаметра элементарных линий к 0, который не зависит от способа разбиения на элементарные линии и выбора точек 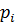 , то он называется КРИ-2 рода от функции
, то он называется КРИ-2 рода от функции 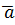 (p), по ориентированной линии L и обозначается
(p), по ориентированной линии L и обозначается 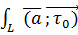 ∂l ;
∂l ;
Теорема 1. Если на ориентир. ограниченной замкнутой гладкой линии L координаты X(x;y;z), Y(x;y;z), Z(x;y;z) непрерывны, то КРИ-2 из опред 3 существует.
Основные свойства КРИ-2 аналогичны свойствам КРИ-1, например:
1) 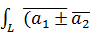 ,
, 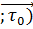 ∂l =
∂l = 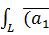
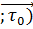 ∂l
∂l 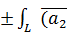
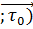 ∂l
∂l
2) 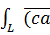
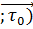 ∂l=
∂l= 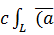
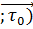 ∂l для
∂l для 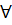 c
c 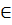 R
R
3) 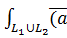
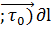 =
= 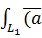
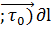 +
+ 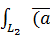
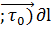
Где 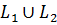 содержит не более одной точки
содержит не более одной точки
4) КРИ-2 обладает рядом специфических св-в
При изменении направления обхода РИ-2 меняет знак: 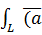
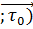 ∂l = -
∂l = - 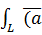
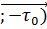 ∂l
∂l
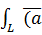
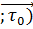 ∂l=
∂l= 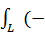
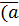
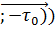 ∂l=
∂l= 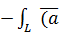
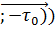 ∂l
∂l
Рассмотрим механическое истолкование КРИ-2:
Пусть сила 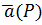 действует вдоль некоторой линии L меняясь как по величине, так и по направлению, т .е.:
действует вдоль некоторой линии L меняясь как по величине, так и по направлению, т .е.: 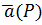 = (X(x;y;z); Y(x;y;z); Z(x;y;z)), тогда работа силы при перемещении по элементарной дуге ∆
= (X(x;y;z); Y(x;y;z); Z(x;y;z)), тогда работа силы при перемещении по элементарной дуге ∆ 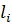 при условии что сила постоянна и равна
при условии что сила постоянна и равна 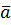
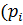 ), где
), где 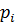 - некоторая точка дуги, равна ∆
- некоторая точка дуги, равна ∆ 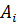 =|
=| 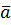
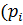 )|- ∆
)|- ∆ 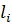 - cos(
- cos( 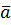
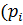 )
) 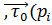 ))= (
))= ( 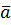
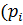 )
) 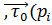 )) ∆
)) ∆ 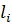
Суммарная работа силы А= 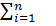 (
( 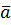
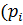 )
) 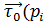 )) ∆
)) ∆ 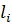
Переходя к пределу 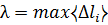 →0 получим А=
→0 получим А= 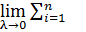 (
( 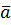
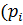 );
); 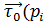 )) ∆
)) ∆ 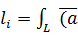
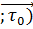 ∂l
∂l
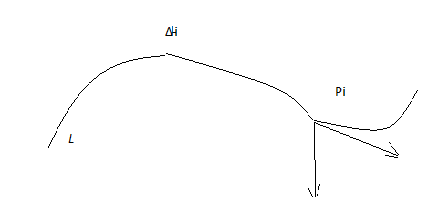
Т.е. с механической точки зрения КРИ-2 представляет собой работу переменной силы вдоль некоторой кривой.
Формула Грина
В случае замкнутого контура КРИ-2 обозначают 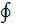 .Если направление обхода контура не указано, то предполагают, что обход конура совершают против часовой стрелки.
.Если направление обхода контура не указано, то предполагают, что обход конура совершают против часовой стрелки.
Пусть в плоскости ХОУ задана область Д ,ограниченная кривой L.
Предположим, что область Д правильная как в направлении оси ОХ, так и в направлении оси ОУ.
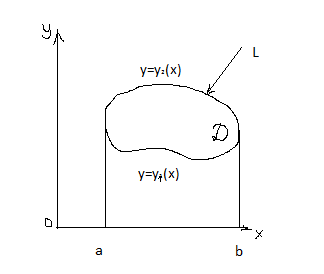 Д:x=a; x=b
Д:x=a; x=b
y=y1(x)
y=y2(x)
Пусть в области Д заданы функции X(x;y) и Y(x;y)-непрерывно дифференцируемые
Тогда:
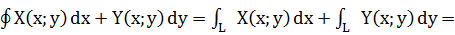 I1+I2
I1+I2
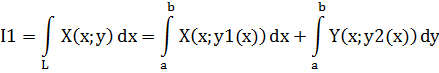
I2= 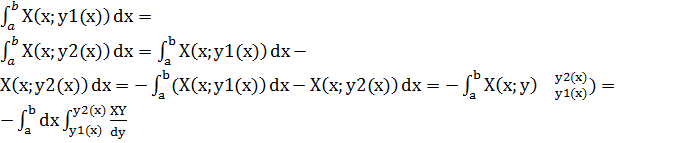
Аналогично
I2= 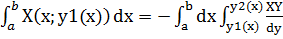
Таким образом
I1=- 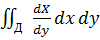
I2= 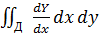
I=- 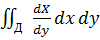 +
+ 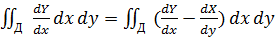
Получим формулу Грина
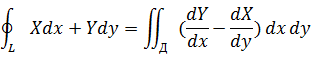
Замечание1 При изменении направления обхода,интеграл в правой части формулы меняет знак
Замечание 2 С помощью формулы Грина можно найти площадь плоской области
Если в скобках во втором интеграле получается 1,то 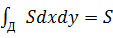
Так,если Y=x/2;X=-4/2,то
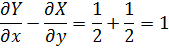
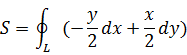
Аналогично при Y=x;X=0,
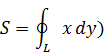
Если Y=0;X=-y
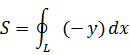
Векторные поля
Определение 1: Векторным полем называется пространство Rn или его часть,в каждом точке j-го определена векторная функция ā=ā(p)
Определение 2:Векторной линией(силовой) векторного поляā=ā(р) называется линия,в каждой точке Pj-й вектор ā(р) направлен по касательной.
Определение 3:Пусть ā=ā(р) – векторное поле R3 .Векторной трубкой называется поверхность,образованная векторными линиями,проходящ.из точки некоторой замкнутой кривой L,не совпадающей ни с одной из векторных линий.
Определение 4:Потоком вектора ā,через поверхность S называется интеграл по поверхности от скалярного произведения вектора поля на единичный вектор нормали к поверхности, т.е. П= 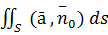
Физический смысл потока: он равен количеству жидкости,протекающей за единицу времени через данную поверхность.
Определение 5:Дивергенцией векторного поля ā(р)(расходимостью) наз.число обознач div āp(p) и равное lim-у отношения потока поля ā(р) из замкнутой поверхности Q к величине объема ∆V,огранич.данной поверхностью,когда ∆V 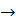 0,т.е. при условии что ∆Q стягивается в т.Р
0,т.е. при условии что ∆Q стягивается в т.Р
div ā(p)= 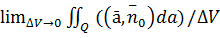
т.о.divā(p) характеризует мощность наход.в точке Р источника,если divā(p)<0,и стока div ā(p)>0.
Если же div ā(p)=0,то в т.Р нет источников и стоков.
Свойства дивергенции:
1. Если ā – постоянный вектор, то div ā= 0.
2. div(c⋅ā) = с⋅divā, где с = const.
3. div (ā + b) = divā + divb т.е. дивергенция суммы двух векторных функций равна сумме дивергенции слагаемых.
4. Если U – скалярная функция, ā – вектор, то div (U⋅ā) = U⋅divā + āgradU.
Док-во (4 св-во):
divUā= 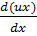 +
+ 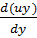 +
+ 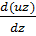 =
= 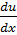 *x
*x 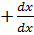 *u+
*u+ 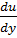 *y+
*y+ 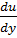 *u+
*u+ 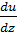 *z+
*z+ 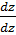 *u=
*u=
u( 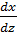 +
+ 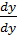 +
+ 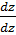 )(x;y;z)*(
)(x;y;z)*( 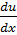 ;
; 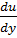 ;
; 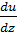 )=u*div ā+ā*grad u.
)=u*div ā+ā*grad u.
Теорема Остроградского-Гаусса:
Если векторная функция ā(р) непрерывно диф-ма в области V,огранич.замкнутой поверхностью Q,то поток векторного поля ā(р) из Q в направлении внешней нормали 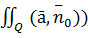 da0=
da0= 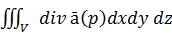
Формула Остроградского-Гаусса означает, что поток векторного поля через
замкнутую поверхность S (в направлении внешней нормали, т.е. изнутри) равен
тройному интегралу от дивергенции этого поля по объему V, ограниченному
данной поверхностью.
Числовые ряды. Необходимый признак сходимости. Простейшие свойства числовых рядов. Сходимость ряда, составленного из членов бесконечной геометрической прогрессии
Пусть а(n)=а1,а2… - числовая последовательность. Выражение вида а1+а2+…+аn = ∑n=1∞an – называется числовым рядом, числа а1, а2 … - члены ряда. аn – общий член ряда.
Сумма конечного числа n первых членов ряда ∑k=1∞ak : a1 + a2 +…+ ak – называется n-ой частичной суммой ряда и обозначается Sn
Если последовательность (Sn )имеет конечный предел S, то это число называется суммой ряда, а ряд – сходящийся. Если предел бесконечен или не существует, то ряд – расходящийся.
Пример 3. Рассмотрим вопрос о сходимости ряда, составленного из членов бесконечной геометрической прогрессии.
b1+ b1q+ b1q2= 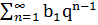 b1≠0
b1≠0
1) если модуль q=1
b1+b1+b1+…+b1 ; Sn=b1+…+b1=n*b1
n
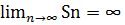 - Ряд расходиться
- Ряд расходиться
2) если модуль q= -1
ряд расходиться
3) если модуль q≠0
Sn= 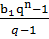
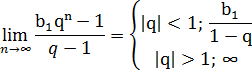
Ответ: ряд сходиться при 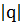 (Sn=
(Sn= 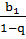 ) и расходиться при
) и расходиться при 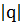 ≥1.
≥1.
Для числового ряда сумма ∑k=1∞ak выражение ak1+ak2+…=∑k=n+1∞a называется n-м остатком ряда. Для сходящегося числового ряда ∑k=1∞ak=∑k=1nak +∑k=n+1∞ak = Sn+rn.
Можно сказать, что последнее условие является не только необходимым , но и достаточным признаком сходимости ряда.
Теорема (необходимый признак сходимости ряда):
если ряд 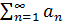 -сходиться, то
-сходиться, то 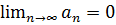 . Пусть
. Пусть 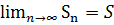 тогда
тогда 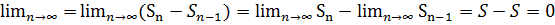
Теорема (достаточный признак расходимости):
если предел 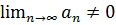 , то ряд
, то ряд 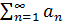 расходиться.
расходиться.
Простейшие свойства сходящихся числовых рядов:
1) Перестановка, отбрасывание или добавление конечного числа членов ряда не влияет на его сходимость.
2) Если ряды 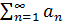 и
и 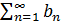 сходятся, то ряд
сходятся, то ряд 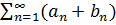 сходиться и его сумма
сходиться и его сумма 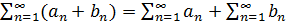 .
.
д-во:
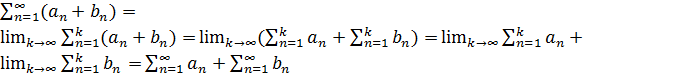
3) Если ряд 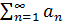 сходиться к числу S, то ряд
сходиться к числу S, то ряд 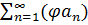 сходиться к числу
сходиться к числу 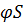 , где
, где 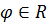 . Док-во аналогично св-ву 2.
. Док-во аналогично св-ву 2.
Операции суммирования рядов и умножения рядов на число называются линейными.
