Дифференциальные уравнения движения материальной точки. Первая и вторая задачи динамики

ΣX = m(d²x/dt²); ΣY = m(d²y/dt²),

где ΣX и ΣY – алгебраические суммы проекций сил, действующих на точку, на соответствующие координатные оси; x и y – текущие координаты точки.

С помощью полученных дифференциальных зависимостей решаются две основные задачи динамики:

• по заданному движению точки определяют действующие на нее силы;
• зная действующие на точку силы, определяют ее движение.

Первая, основная задача динамики точки заключается в том, чтобы по заданному закону движения материальной точки определить результирующую или одну из составляющих сил, действующих на эту точку.

При наличии нескольких сил, действующих на точку, второй закон Ньютона дает основное уравнение динамики точки

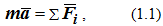
В зависимости от способа задания движения точки, это уравнение можно записать по-разному.

Для векторного способа задания движения

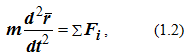
где r = r (t) – радиус-вектор, определяющий положение точки по отношению к выбранной системе отсчета.

Для координатного способа задания движения точки

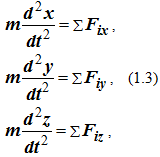
где x = x (t), y = y (t), z = z (t) – координаты точки, заданные как функции времени.

Вторая, основная задача динамики точки заключается в том, чтобы по заданным силам, действующим на точку, определить ее движение.

Пусть на материальную точку действует некоторая система сил и требуется определить движение точки под действием этих сил.

Уравнение второго основного закона динамики для материальной точки массой m запишется в виде

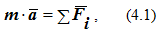
где a – ускорение точки;

F_i – силы, действующие на точку, включая реакции связей.

Спроектировав уравнение (4.1) на декартовы оси координат, получим систему из трех уравнений

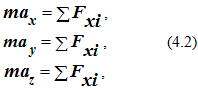
где a_x , a_y, a_z – проекции ускорения точки на декартовы оси координат;

F_x, F_y, F_z – проекция i -й силы на соответствующую ось.

Учитывая, что

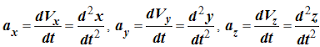
Свободные колебания материальной точки. Влияние постоянной силы на свободное колебание

Свободные колебания (или собственные колебания) — это колебания колебательной системы, совершаемые только благодаря первоначально сообщенной энергии (потенциальной или кинетической) при отсутствии внешних воздействий

Дифференциальное уравнение свободных колебаний при отсутствии сопротивления:

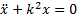
Общее решение этого уравнения имеет вид 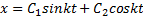, где

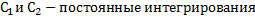
В случае, когда действующая на материальную точку позиционная сила стремиться вернуть ее в исходное положение, движение точки будет носить колебательный характер. Такую силу принято называть восстанавливающей.

Под действием восстанавливающей силы материальная точка совершает движение по синусоидальному закону, т.е. гармоническое колебательное движение.

Постоянная сила Р не изменяет характера колебаний, совершаемых точкой под действием восстанавливающей силы F, а только смещает центр этих колебаний в сторону действия силы Р на величину ста­тического отклонения 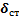.