Наибольшее и наименьшее значение ФНЛ заданной на ограниченной

Постановка задачи.Пусть на плоскости 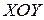замкнутая ограниченная область 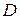задаётся системой неравенств вида

.

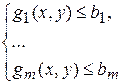Требуется найти в области 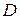точки, в которых функция 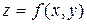принимает наибольшее и наименьшее значения.

Важной является задача нахождения экстремума, математическая модель которой содержит линейныеограничения (уравнения, неравенства) и линейную функцию .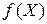

Постановка задачи.Найти наибольшее и наименьшее значения функции

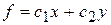(1)

при ограничениях

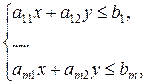(2)

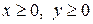. (3)

Поскольку для линейной функции многих переменных нет критических точек внутри области 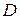, то оптимальное решение, доставляющее целевой функции экстремум, достигается только на границе области. Для области, заданной линейными ограничениями, точками возможного экстремума являются угловые точки. Это позволяет рассматривать решение задачи графическим методом.

Условный экстремул метод множителей лангранжа

Для начала рассмотрим случай функции двух переменных. Условным экстремумом функции z=f(x,y) в точке M0(x0;y0) называется экстремум этой функции, достигнутый при условии, что переменные x и y в окрестности данной точки удовлетворяют уравнению связи φ(x,y)=0.

Название «условный» экстремум связано с тем, что на переменные наложено дополнительное условие φ(x,y)=0. Если из уравнения связи можно выразить одну переменную через другую, то задача определения условного экстремума сводится к задаче на обычный экстремум функции одной переменной. Например, если из уравнения связи следует y=ψ(x), то подставив y=ψ(x) в z=f(x,y), получим функцию одной переменной z=f(x,ψ(x)). В общем случае, однако, такой метод малопригоден, поэтому требуется введение нового алгоритма.

Метод множителей Лагранжа для функций двух переменных.

Метод множителей Лагранжа состоит в том, что для отыскания условного экстремума составляют функцию Лагранжа: F(x,y)=f(x,y)+λφ(x,y) (параметр λ называют множителем Лагранжа). Необходимые условия экстремума задаются системой уравнений, из которой определяются стационарные точки:

⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪∂F∂x=0;∂F∂y=0;φ(x,y)=0.

Достаточным условием, из которого можно выяснить характер экстремума, служит знак d2F=F′′xxdx2+2F′′xydxdy+F′′yydy2. Если в стационарной точке d2F>0, то функция z=f(x,y) имеет в данной точке условный минимум, если же d2F<0, то условный максимум.

Есть и другой способ для определения характера экстремума. Из уравнения связи получаем: φ′xdx+φ′ydy=0, dy=−φ′xφ′ydx, поэтому в любой стационарной точке имеем:

d2F=F′′xxdx2+2F′′xydxdy+F′′yydy2=F′′xxdx2+2F′′xydx(−φ′xφ′ydx)+F′′yy(−φ′xφ′ydx)2==−dx2(φ′y)2⋅(−(φ′y)2F′′xx+2φ′xφ′yF′′xy−(φ′x)2F′′yy)

Второй сомножитель (расположенный в скобке) можно представить в такой форме:

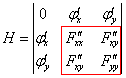
Красным цветом выделены элементы определителя ∣∣∣∣F′′xxF′′xyF′′xyF′′yy∣∣∣∣, который является гессианом функции Лагранжа. Если H>0, то d2F<0, что указывает на условный максимум. Аналогично, при H<0 имеем d2F>0, т.е. имеем условный минимум функции z=f(x,y).