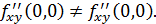Частные производные и дифференциалы высших порядков

Частные производные высших порядков

Частные производные 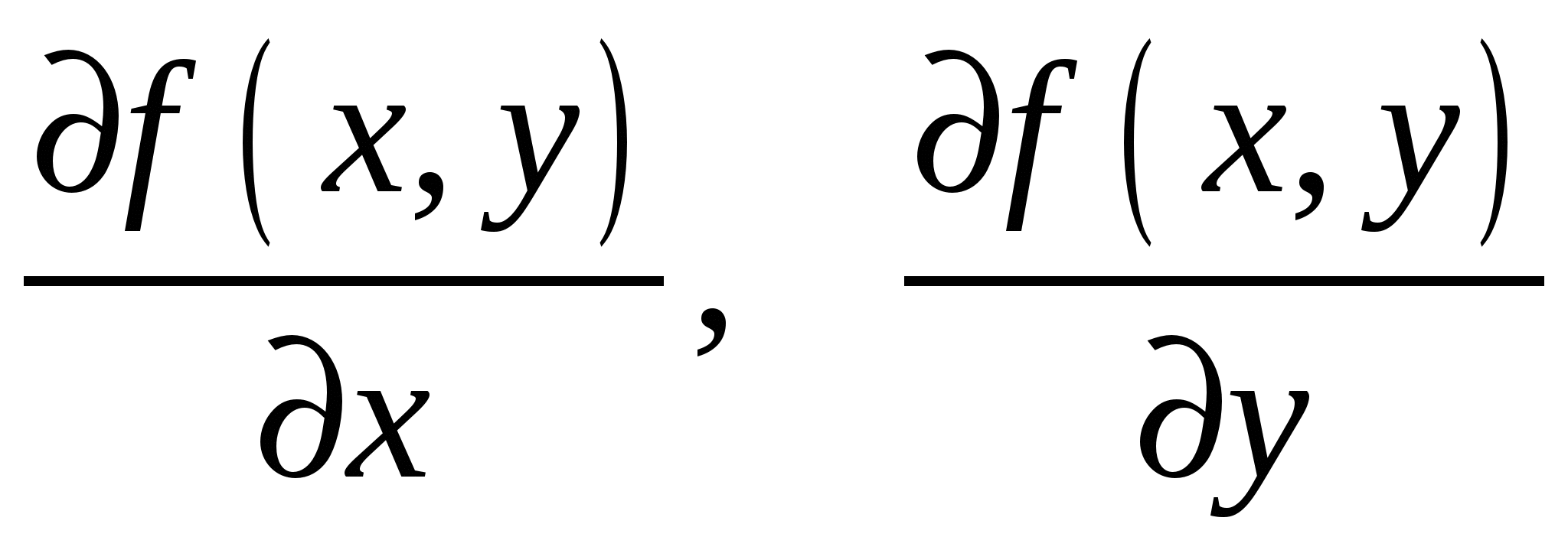называютчастными производными первого порядка. Их можно рассматривать как функции от 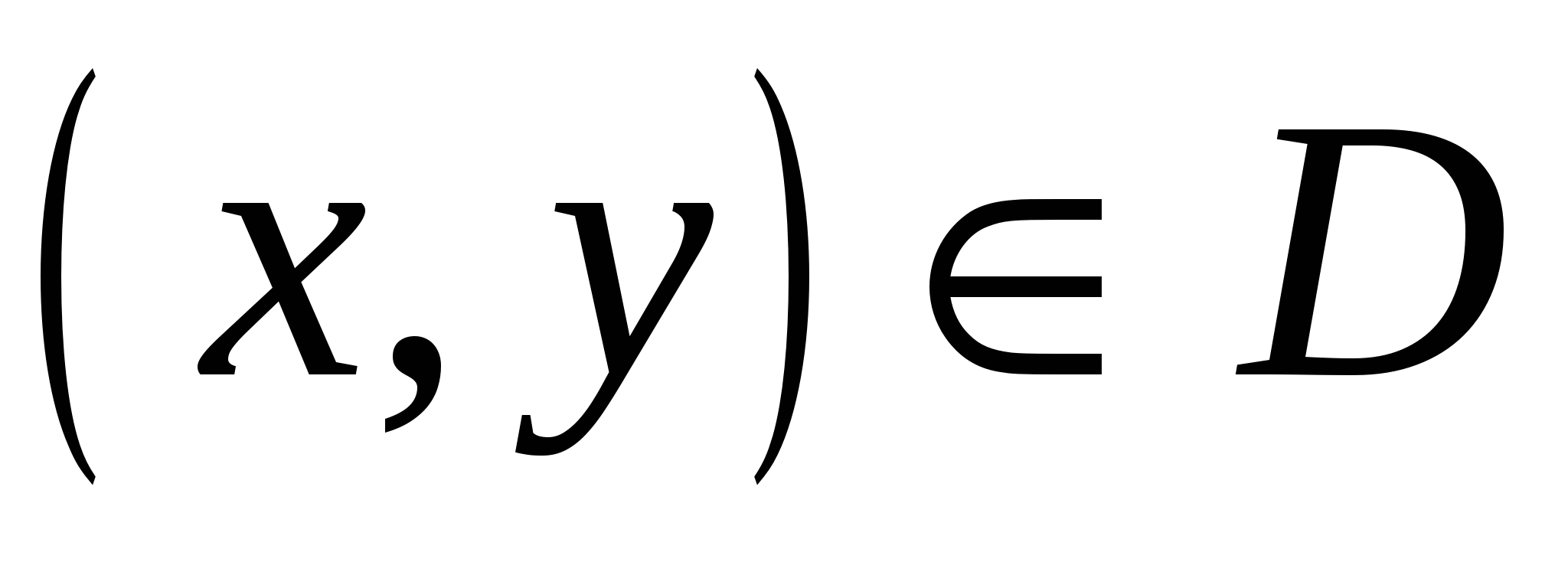. Эти функции в свою очередь могут иметь частные производные, которые называютсячастными производными второго порядка. Они обозначаются следующим образом: .

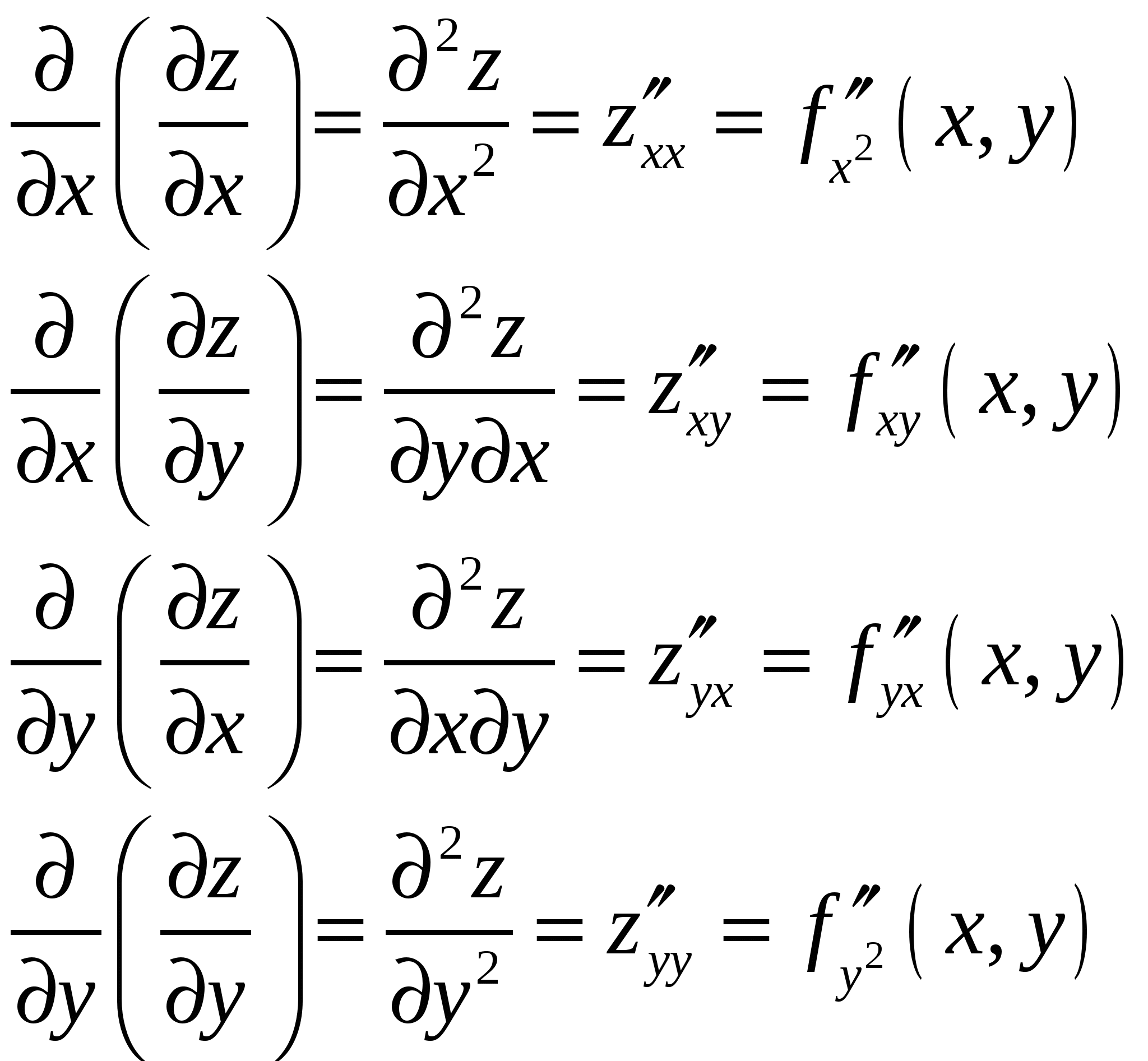Аналогично определяются частные производные 2-го и 3-го и т.д. порядков.

Так 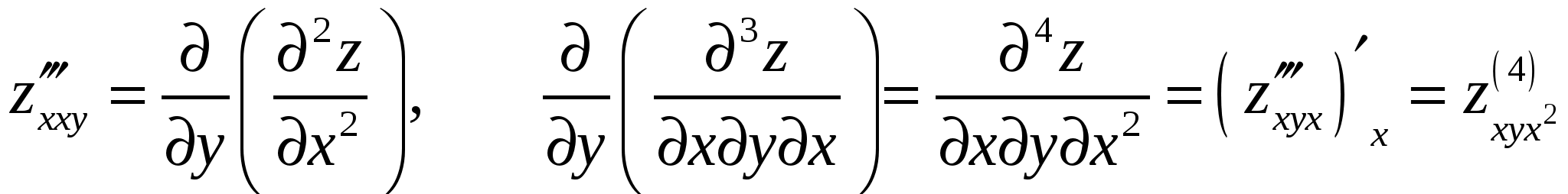и т.д.

Частная производная второго и более высокого порядка, взятая по различным переменным называется смешанной частной производной

Теорема 2

Смешанные производные второго порядка равны, если они непрерывны: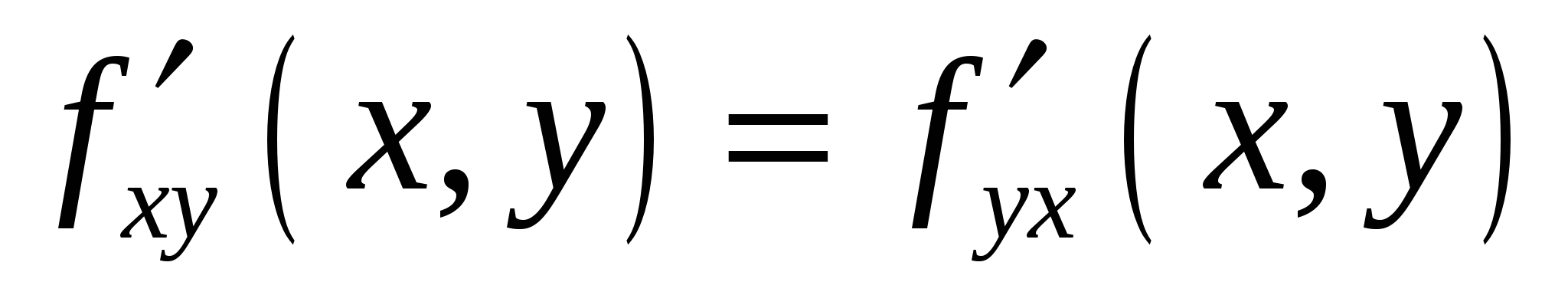

Следствие

Смешанные производные высших порядков равны, если непрерывны и получены по одним и тем же переменным одинаковое число раз, но может быть в разной последовательности.

3.2 Дифференциалы высших порядков

Заметим, что для функции нескольких переменных справедливы те же общие правила дифференцирования, что и для функции одной переменной.

Пусть 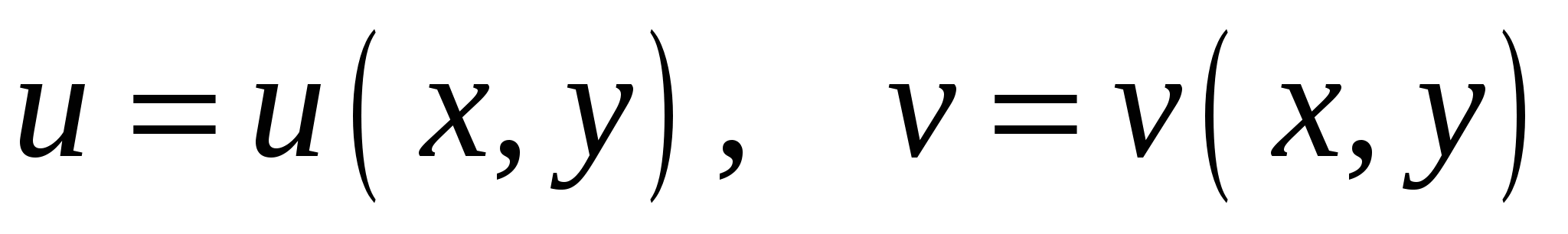, тогда

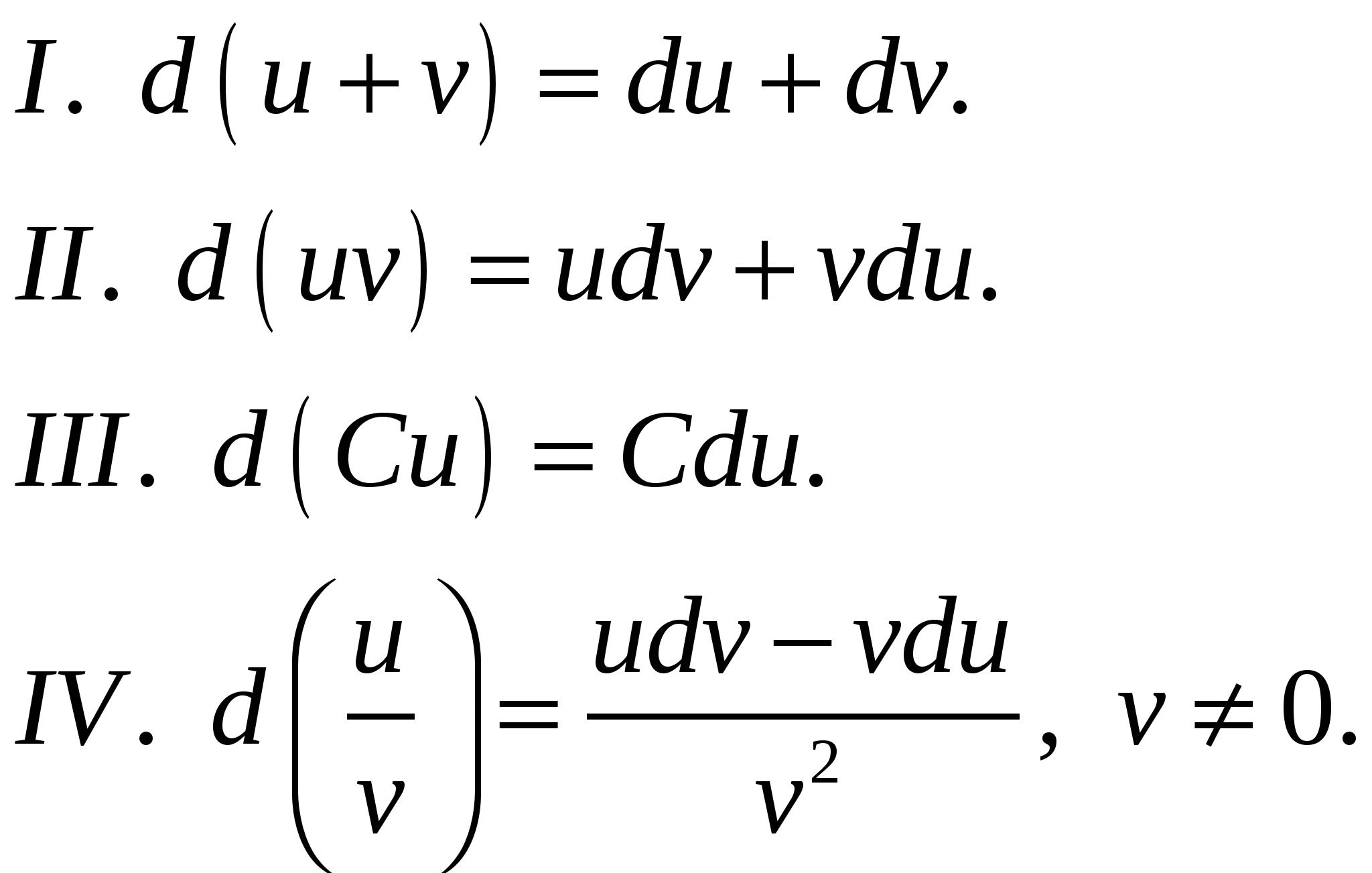
Например, имеем:

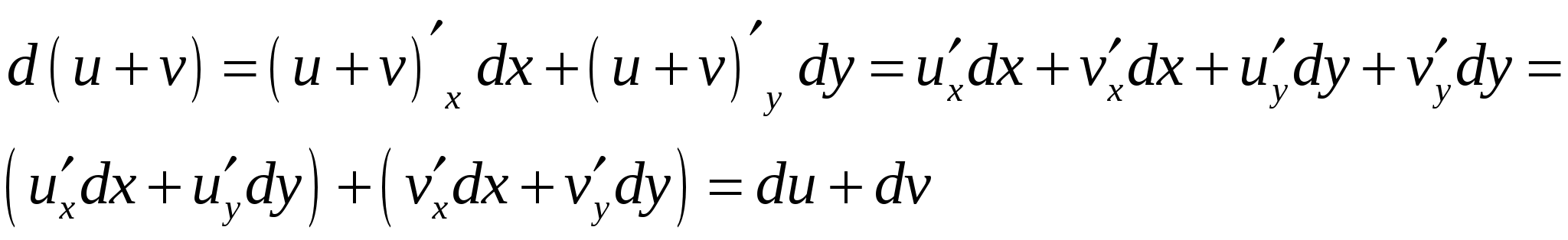
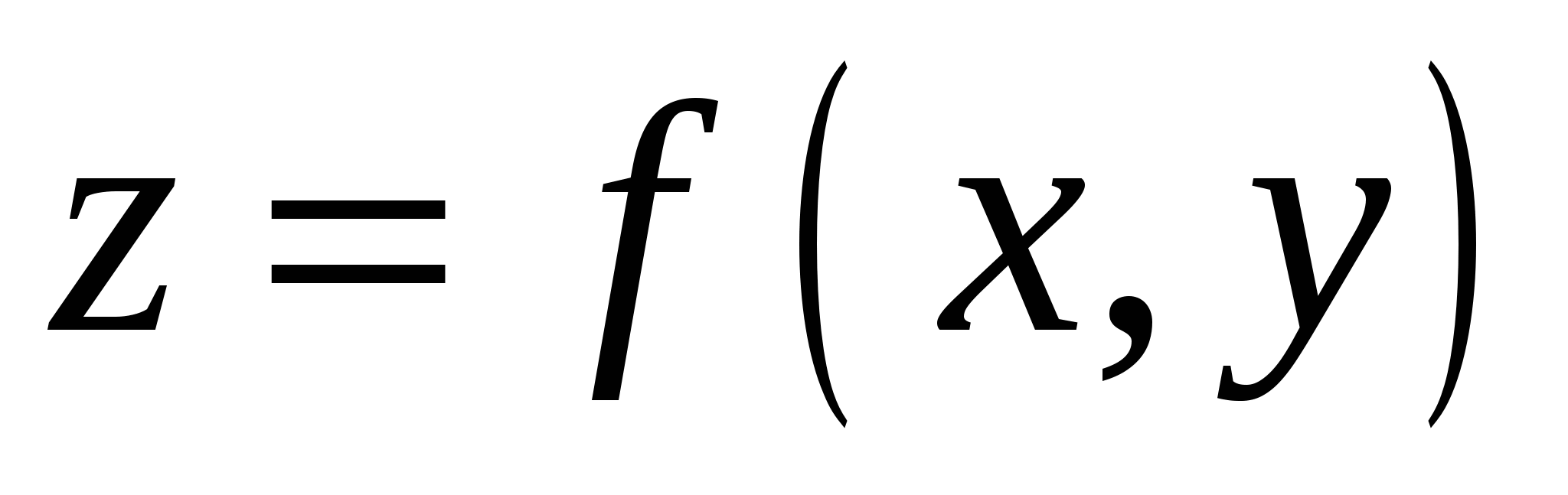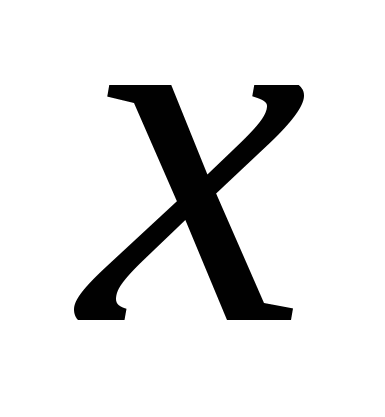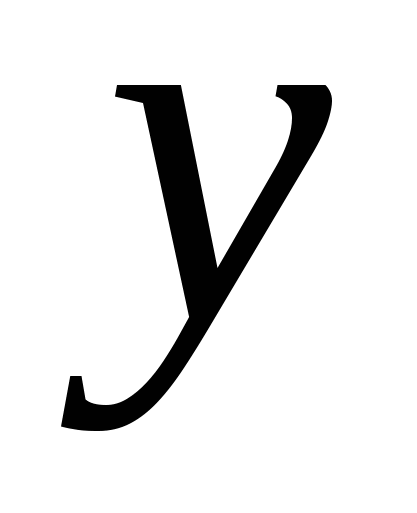Пусть имеется функция независимых переменных и , обладающая непрерывными частными производными второго порядка. Рассмотрим её полный дифференциал

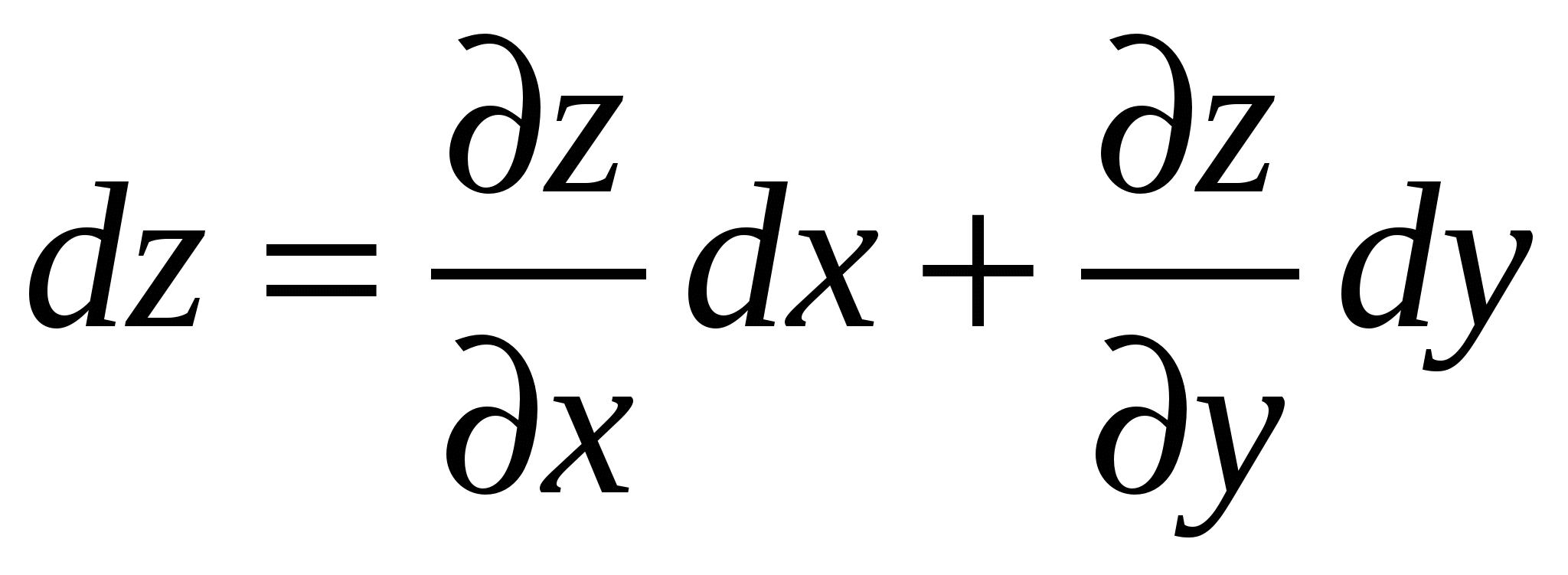(1)

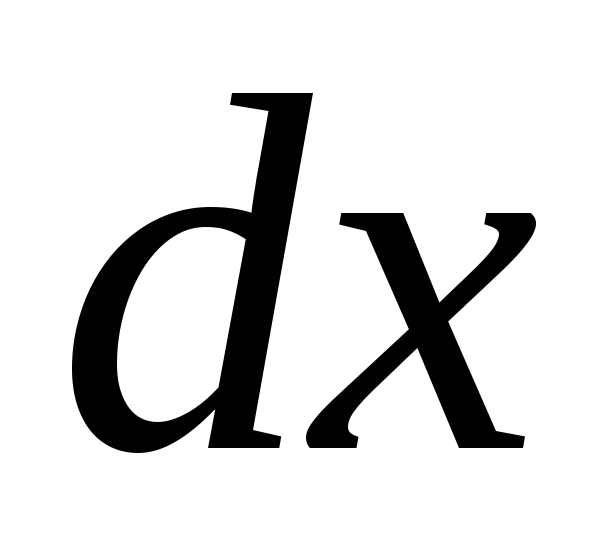( и 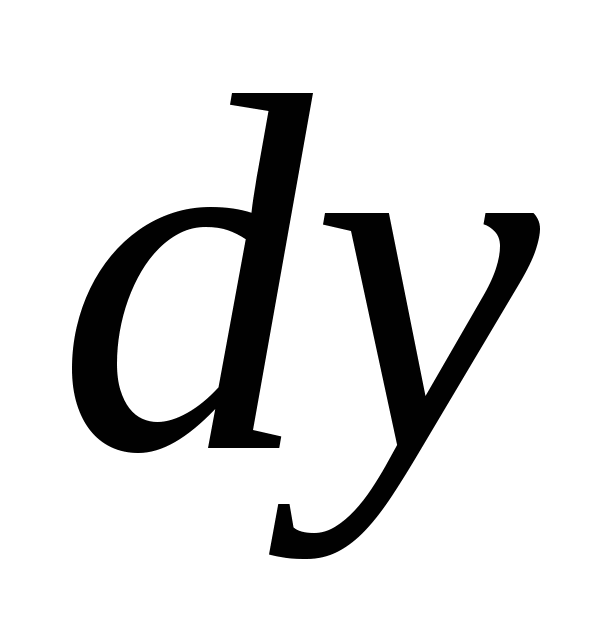– произвольные приращения), который назовемполным дифференциалом первого порядка(или, кратко,первым дифференциалом).

Так как 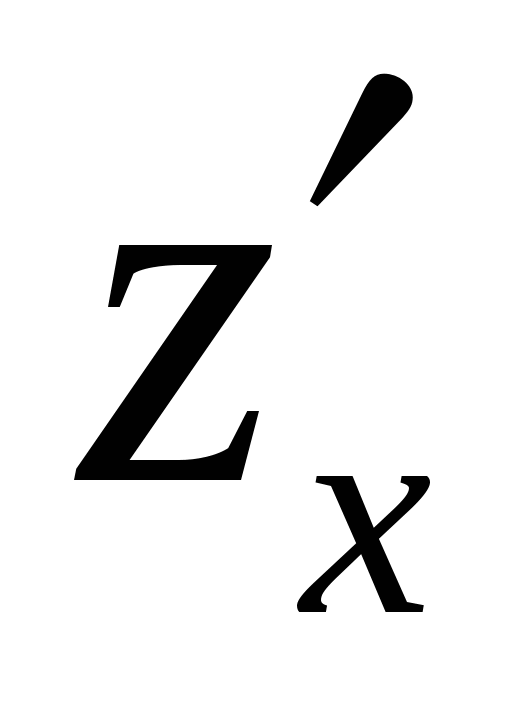и 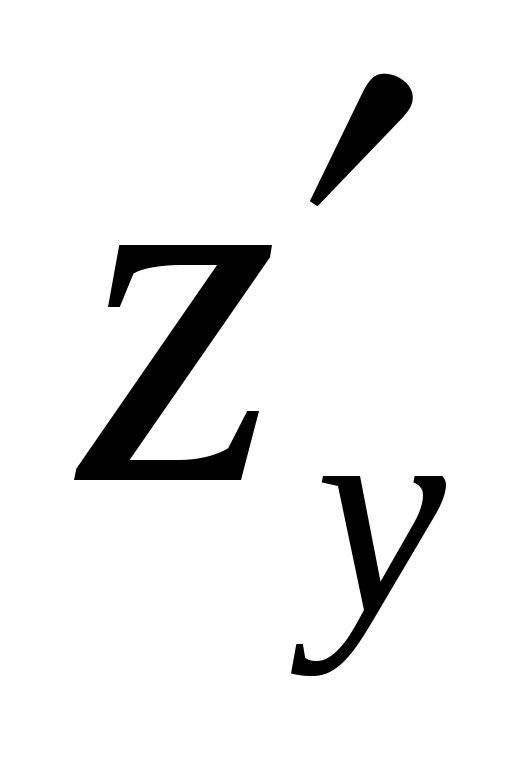по предположению имеют непрерывные частные производные первого порядка, то от функции , в свою очередь, можно взять полный дифференциал 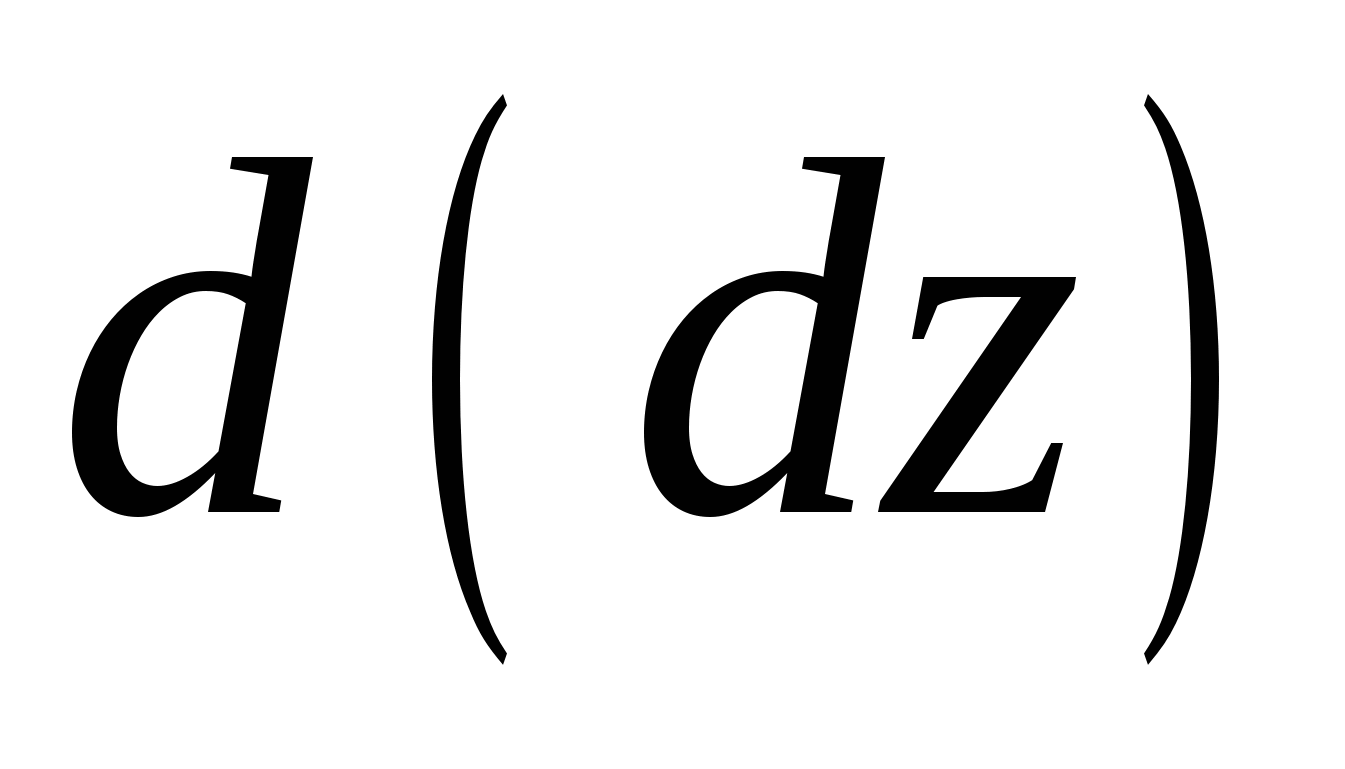. Так получимполный дифференциал второго порядка(или кратковторой дифференциал), который обозначается 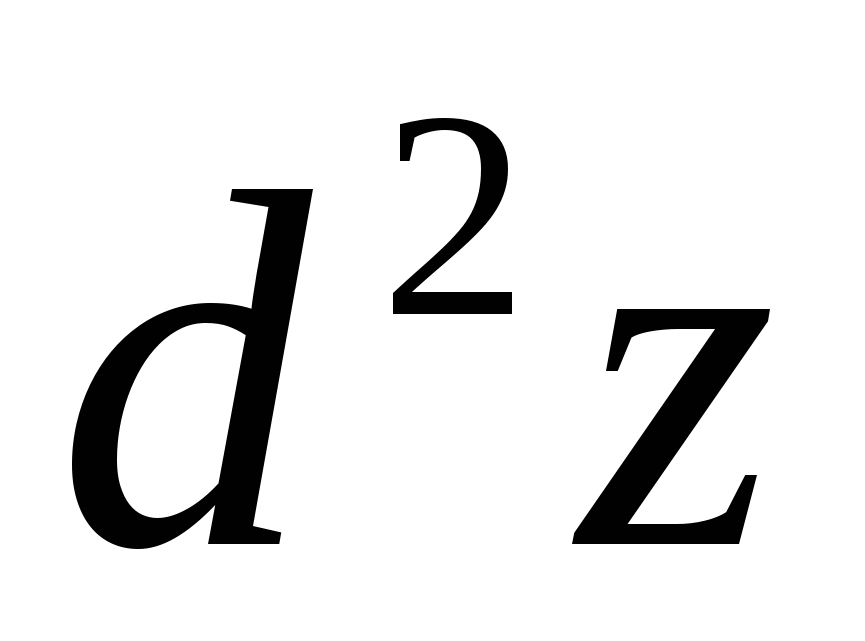. И т.д.

Найдем выражение для второго дифференциала

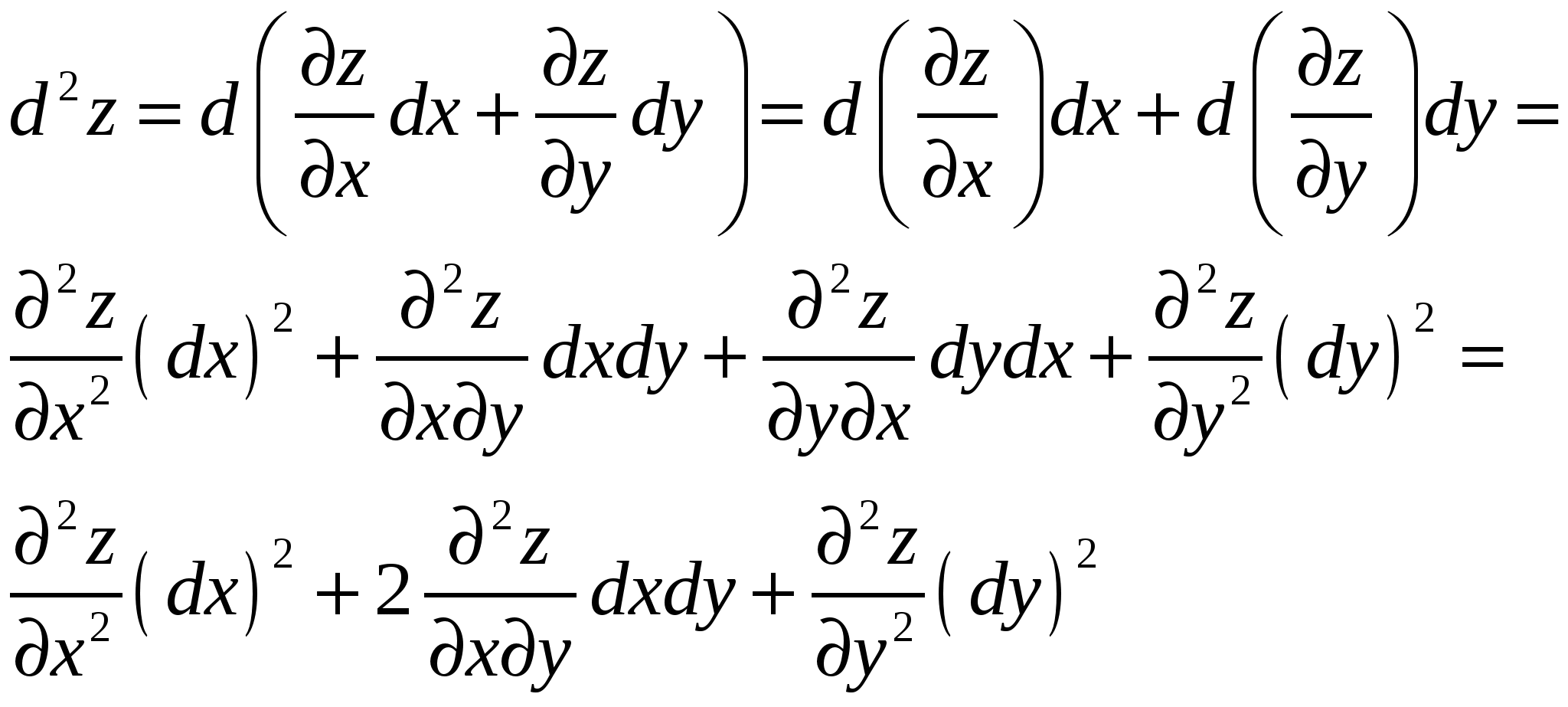(2)

(здесь ).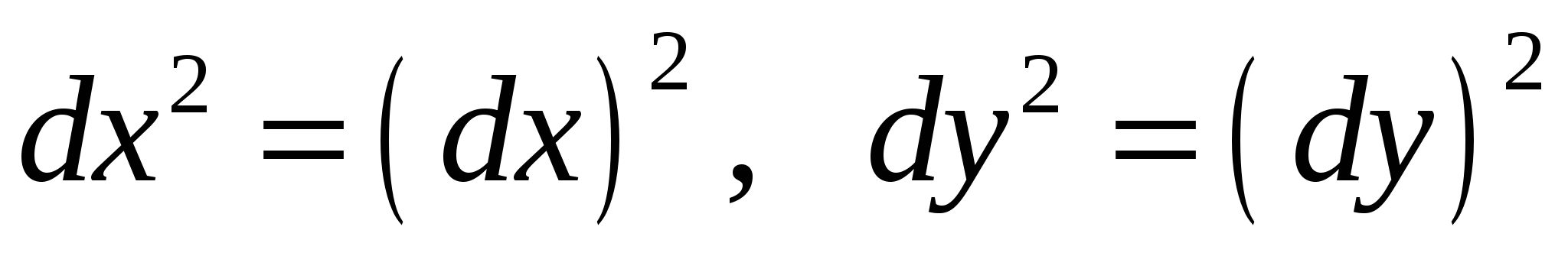

Формула (2) обобщается на случай дифференциала -го порядка.

3.Формула Тейлора для функции двух переменных

Пусть имеется функция независимых переменных и , имеющая непрерывные частные производные всех порядков до 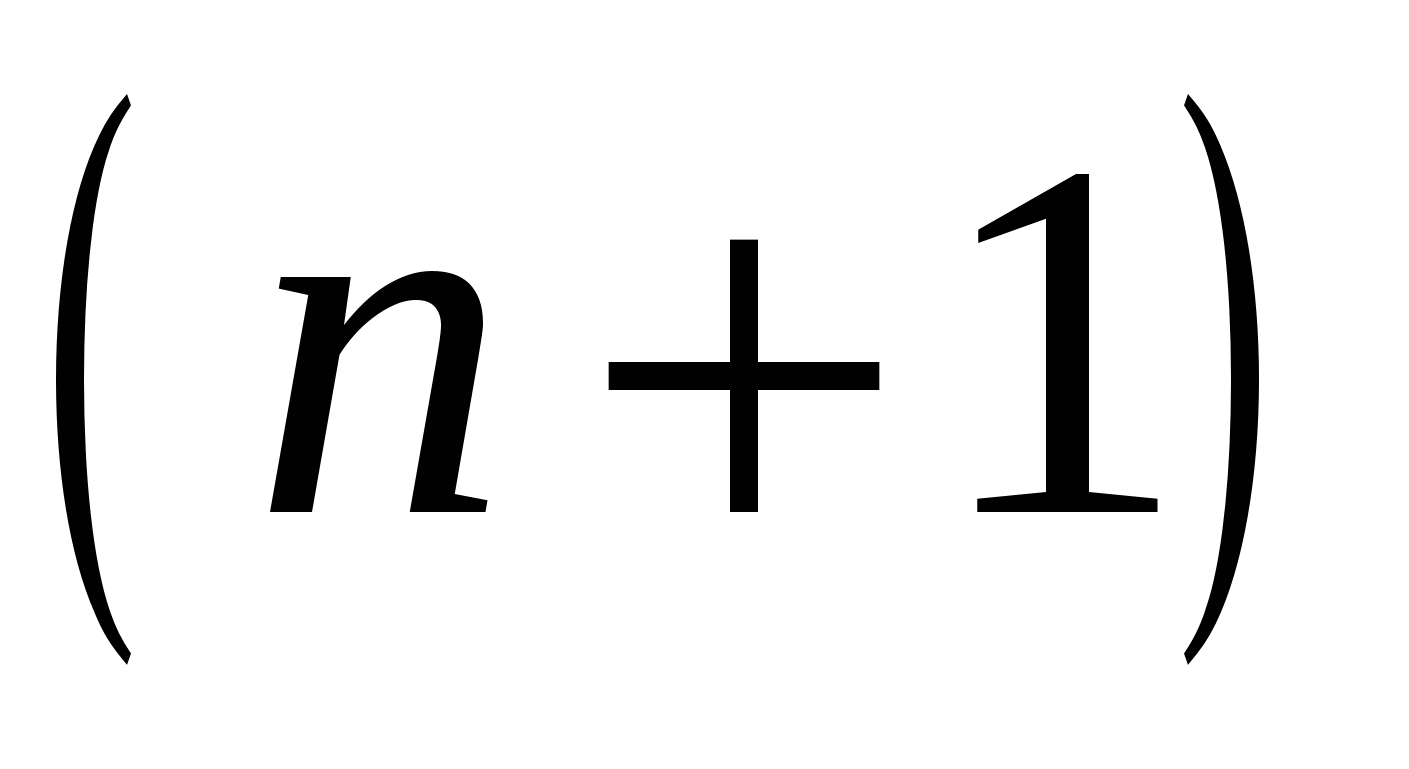-го включительно в некоторой окрестности точки 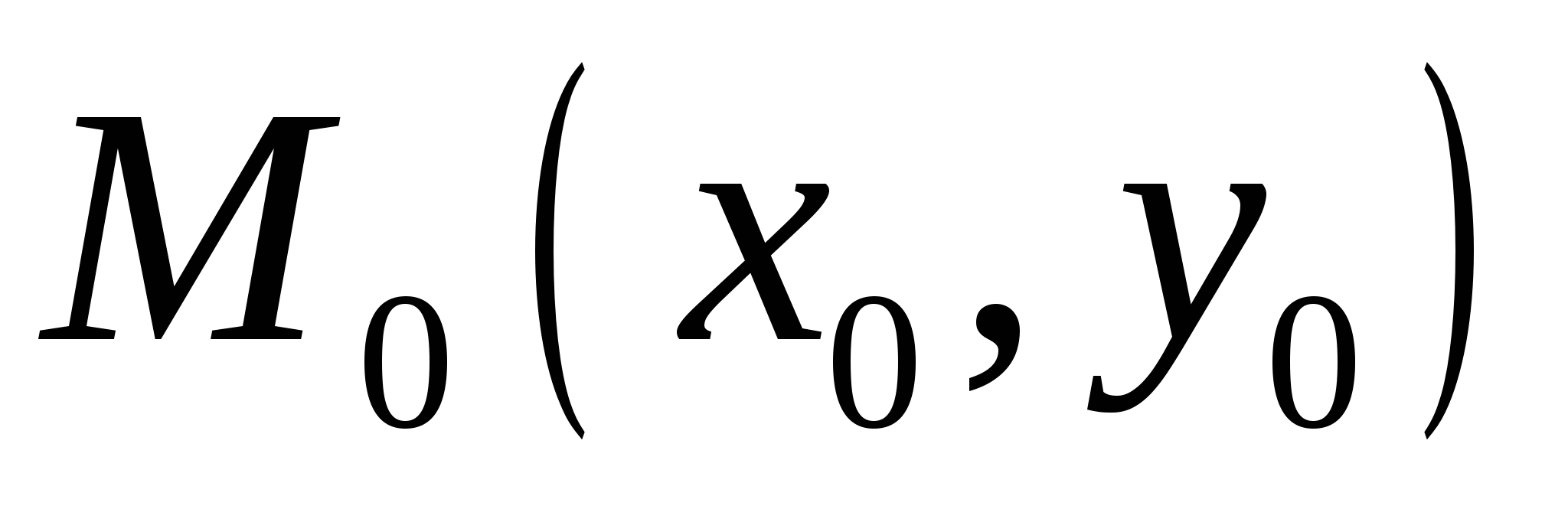. Пусть точка 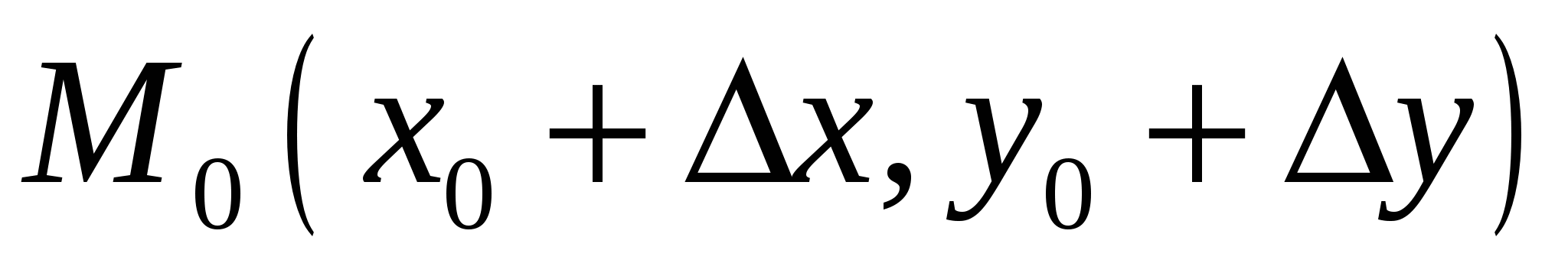принадлежит этой окрестности. Определим на отрезке 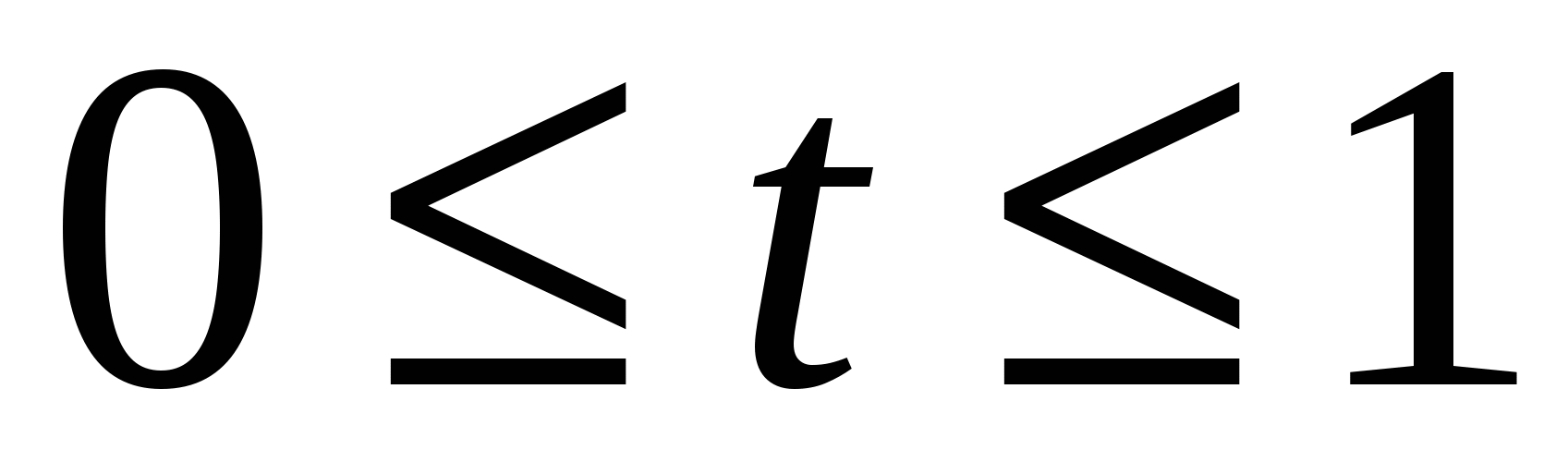вспомогательную функцию :

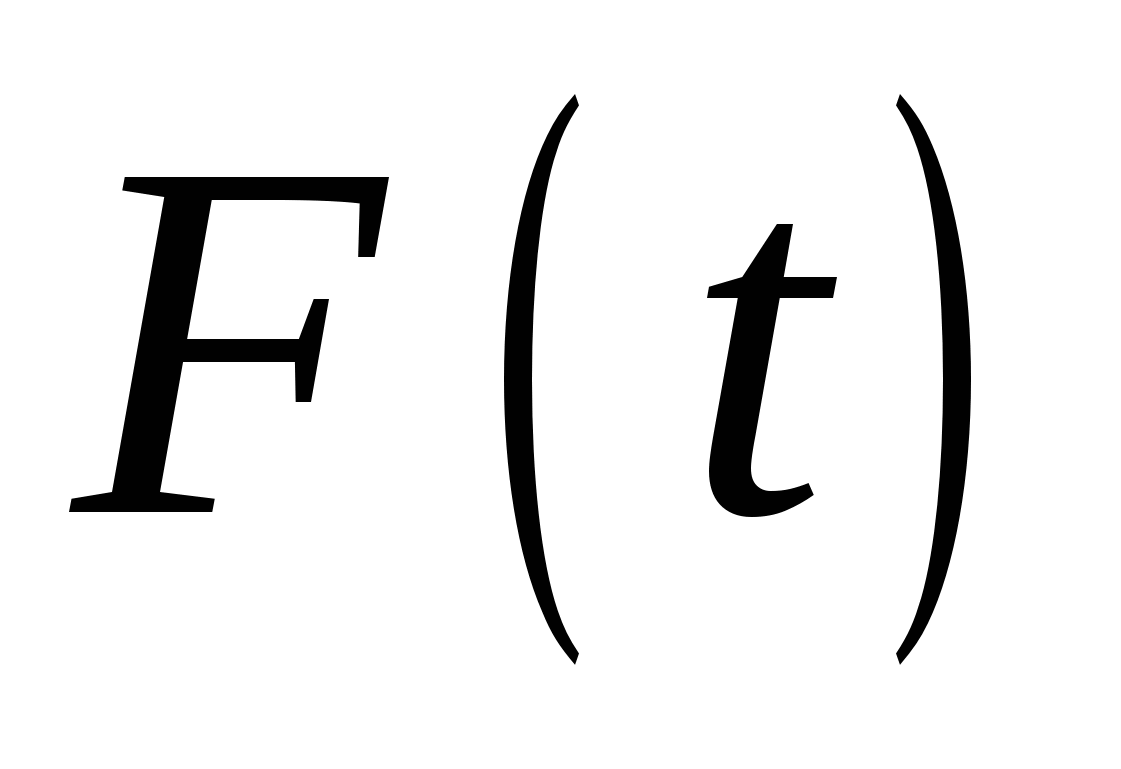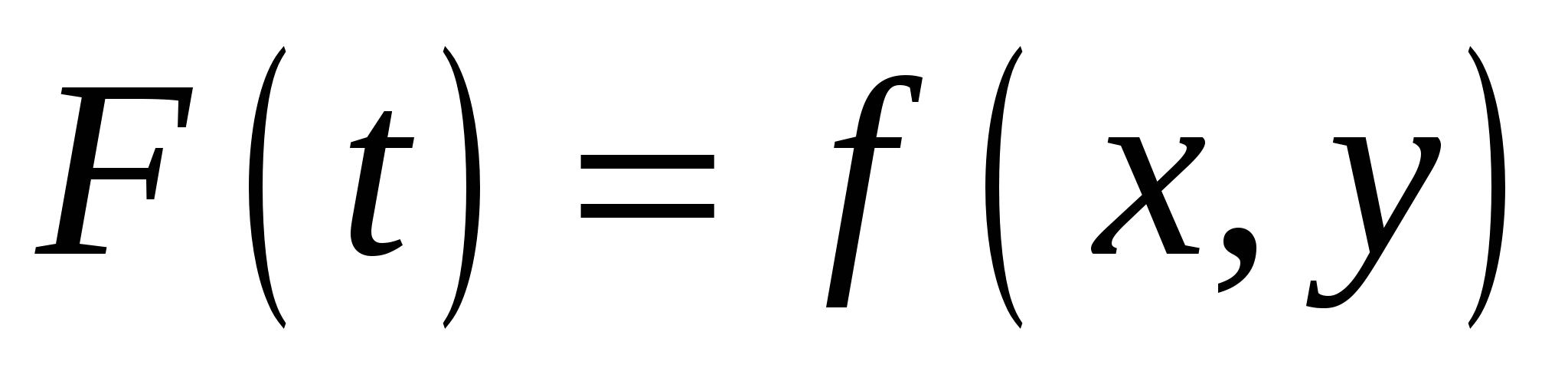, (3)

где 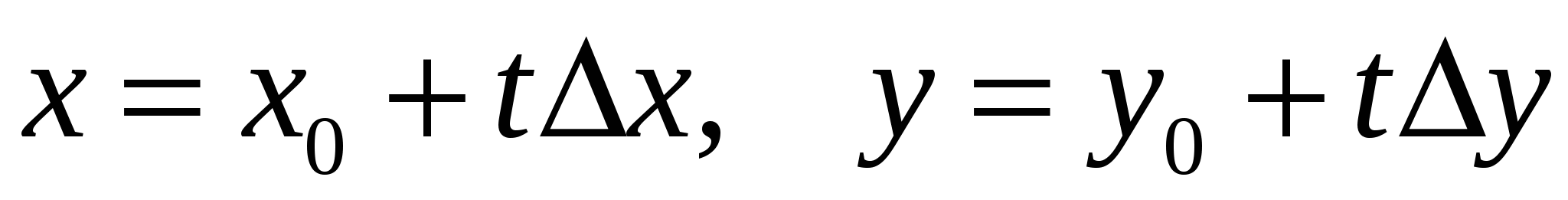. Согласно формуле Тейлора, имеем:

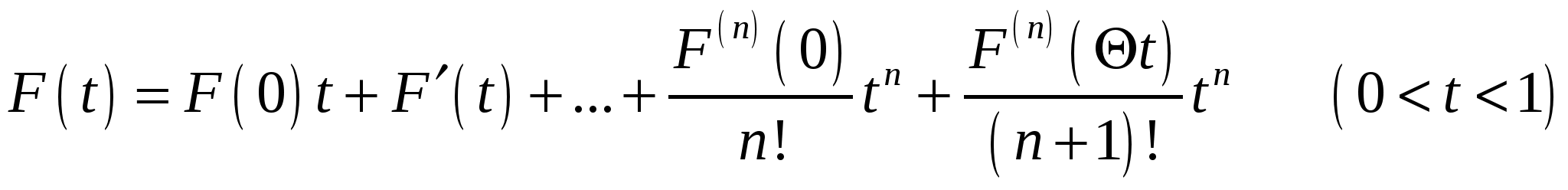(4)

Вычислим коэффициенты формула (4) с помощью равенства (3). При 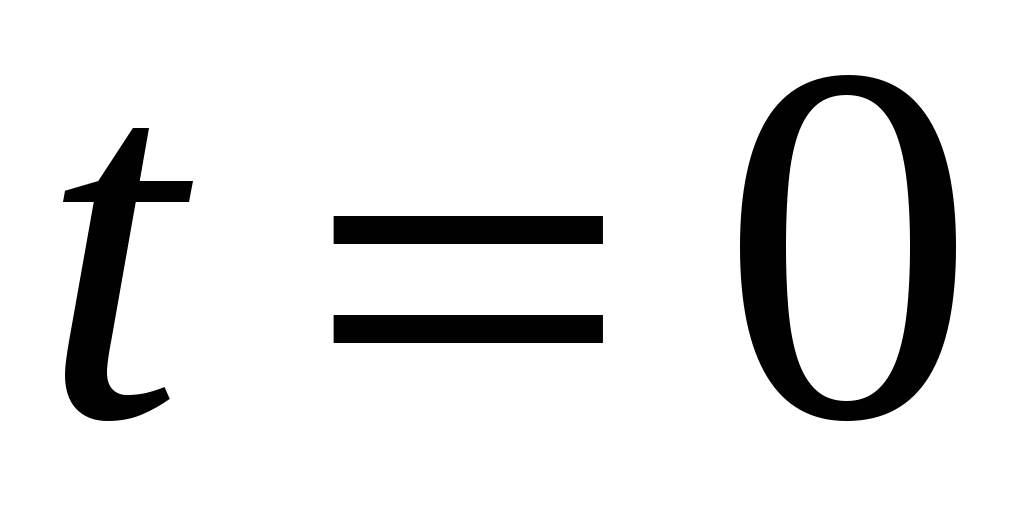имеем 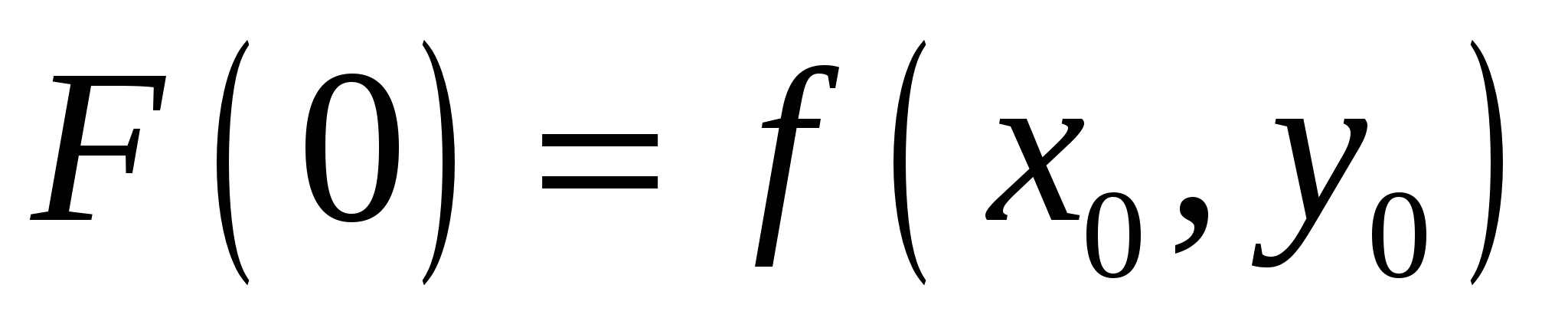. Дифференцируя сложную функцию по 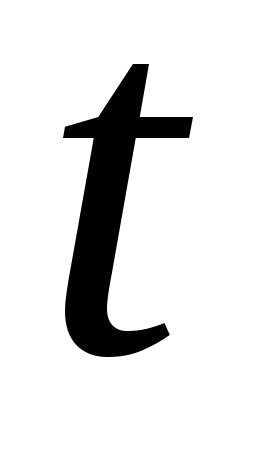получим:

,

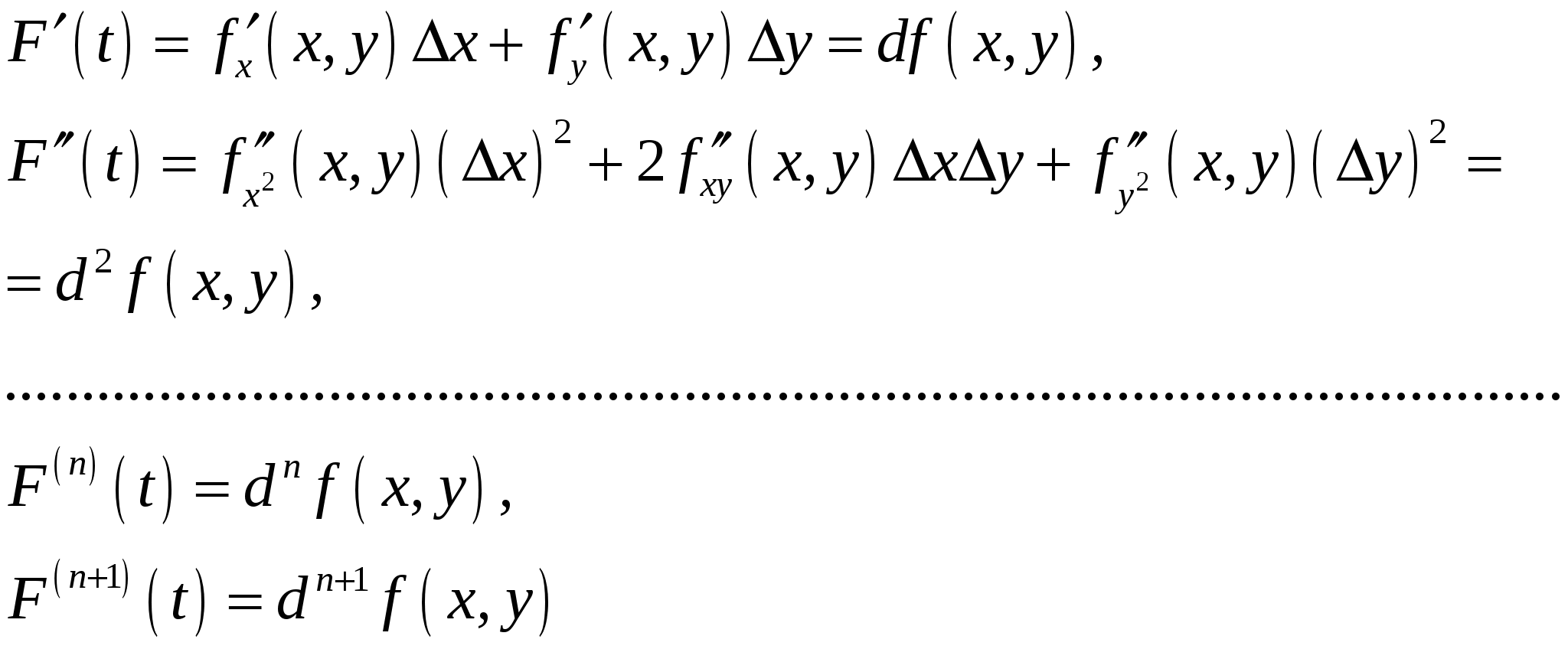Заменив в последнем равенстве на , а в остальных положим , найдем:

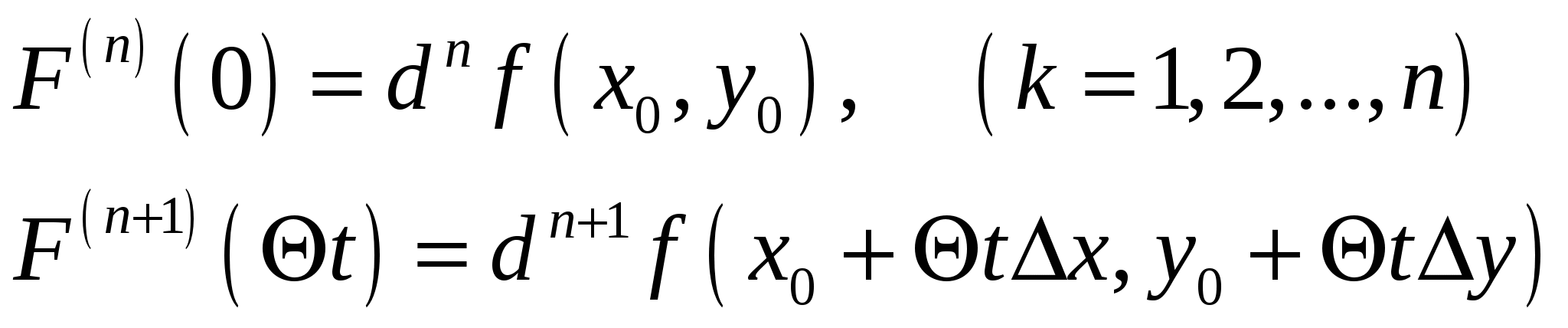
Если подставим найденные выражения в равенство (4) и затем положим 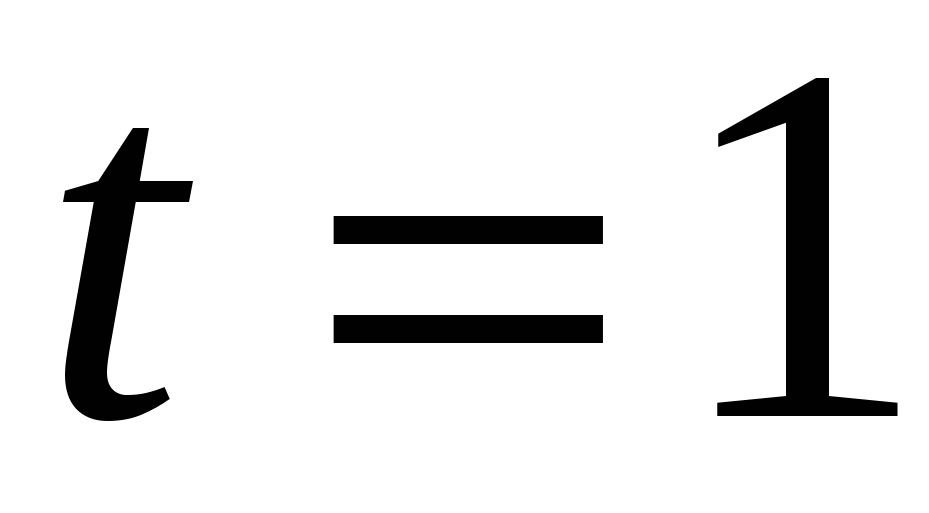, то получим для формулу Тейлора:

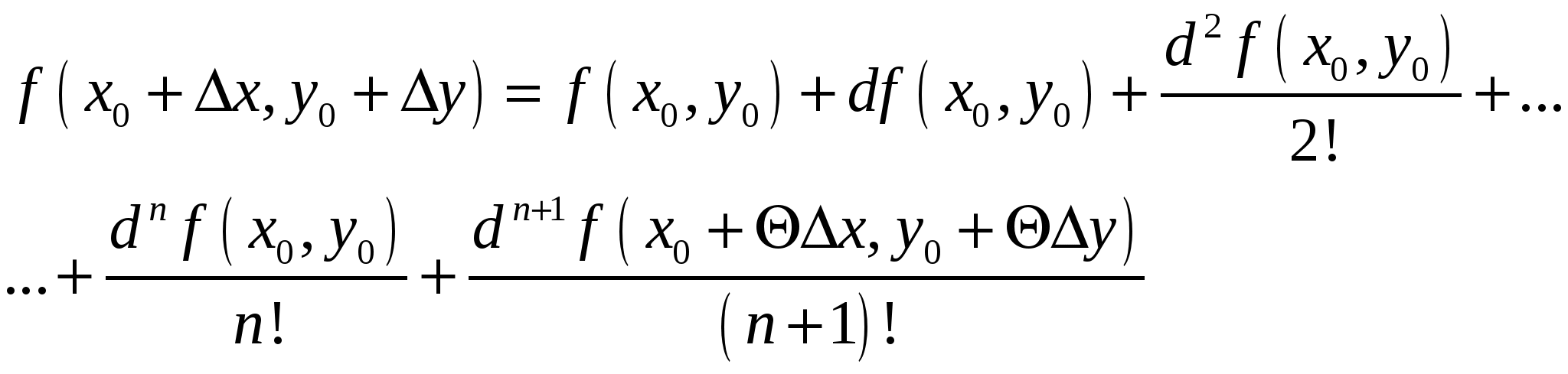
Теорема о смешанных производных

Теорема ( без доказательства).

Пусть функция 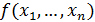определена в области 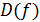. Пусть существуют и непрерывны все частные производные до k -го порядка включительно в области 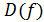. Тогда смешанные производные до -го порядка не зависят от порядка дифференцирования.

Пример.Рассмотрим функцию двух переменных, у которой смешанные производные второго порядка существуют, но не равны в точке (0,0):

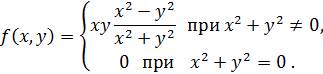
Имеем:

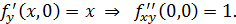
Видим, что