Статистические свойства энтропии

Фазовый объем системы, состоящей из независимых подсистем 1 и 2, по определению равен произведению объемов, которые они занимают:

,

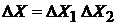тогда из (2.13)

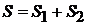. (2.13б)

Энтропия аддитивная величина – энтропия системы равна сумме энтропий независимых подсистем.

Из

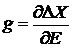, (2.9а)

находим

.

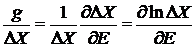Используем

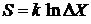, (2.13)

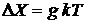, (2.14)

получаем

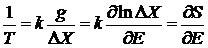. (2.14а)

Следовательно:

1. Число микросостояний и фазовый объем системы увеличиваются экспоненциально с ростом энтропии согласно

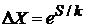. (2.13а)

Чем больше микросостояний, тем меньше информации о системе. Увеличение энтропии означает уменьшение информации о системе и увеличение ее хаотичности. Для контроля и управления необходимо снижать энтропию системы.

2. Чем ниже температура, тем быстрее возрастает энтропия с ростом энергии системы согласно (2.14а). Для лучшей контролируемости системы нужно снижать ее температуру и использовать переходы с малой энергией.

ПРИМЕР 1

Атом массой m с энергией e находится в объеме V, где все точки и направления равноправны. Найти энергетическую плотность состояний. Получить температуру и давление, создаваемые фазовым ансамблем. Рассмотреть случай, когда в объеме находятся N атомов идеального газа.

Энергия и импульс атома связаны соотношением

.

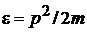Фазовый ансамбль находится в импульсном пространстве на сфере радиусом

.

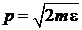Микросостояния фазового ансамбля отличаются направлениями вектора импульса. Число микросостояний, или фазовый объем

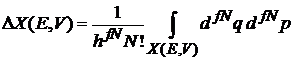
при ,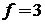

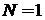
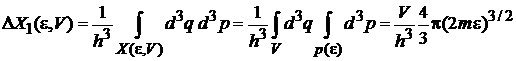. (2.2а)

Учтена независимость импульса от координат при отсутствии внешнего поля. Из

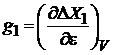(2.9а)

получаем

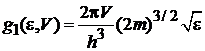. (П.2.5)

Плотность состояний классического газа пропорциональна корню квадратному из энергии.

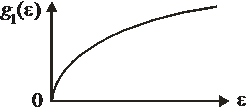
Из

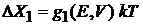(2.14)

находим

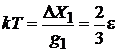. (П.2.6)

Температура пропорциональна энергии частицы.

При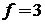

,

.

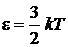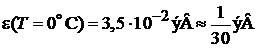Из

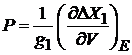, (2.12)

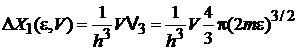, (2.2а)

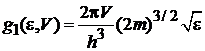, (П.2.5)

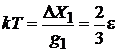, (П.2.6)

получаем давление, создаваемой фазовым ансамблем, соответствующим одной частице:

.

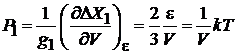Получили уравнение идеального газа 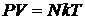для одной частицы.

Азот N₂:

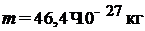
при

, ,

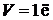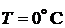имеет

, .

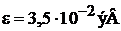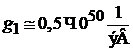На интервале энергии 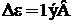находятся 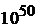уровней, следовательно, классический газ имеет квазинепрерывный спектр.

Для N частиц с полной энергией E

.

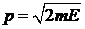Для объема импульсного пространства в виде шара размерностью 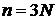используем

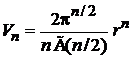, (П.2.1)

получаем

,

,

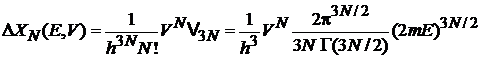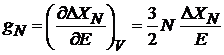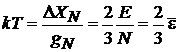
– температура пропорциональна средней энергии частицы.

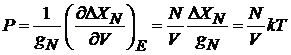
– уравнение идеального газа .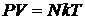

ПРИМЕР 2

Система из N одномерных гармонических осцилляторов с полной энергией Е. Найти энергетическую плотность состояний и среднюю энергию осциллятора.

Полная энергия системы

,

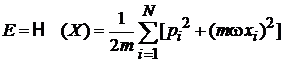тогда

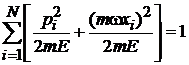
– уравнение эллипсоида в 2N-мерном пространстве,

N полуосей – ,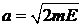

N полуосей – ,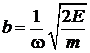

.

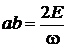Фазовый объем системы пропорционален объему эллипсоида

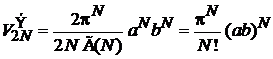. (П.2.1а)

Число микросостояний

,

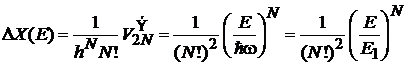где 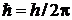; 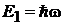– интервал эквидистантного спектра осциллятора.

Из

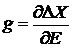(2.9а)

получаем энергетическую плотность состояний

.

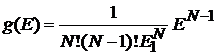Из

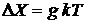(2.14)

находим

.

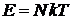Средняя энергия осциллятора

.

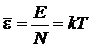Каноническое распределение

Объект – равновесный идеальный газ из N частиц в объеме V в термостате с температурой Т.