Движение заряженной частицы в электромагнитном поле в формализме Лагранжа

Пусть частица с зарядом e находится в электромагнитном иоле, заданном скалярным φ(r, t) и векторным A(r,t) потен­циалами. Электрическое и магнитное поля Е и B связаны с потенциалами соотношениями

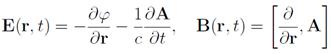
Где c- скорость света. Нетрудно показать, что уравнение Лагранжа

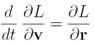
совпадают с известными уравнениями движения

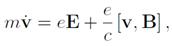
если выбрать функцию Лагранжа в виде

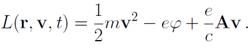
В функции Лагранжа слагаемые 1/2mv² и еср — это обычные кинетическая и потенциальная энергии частицы, а послед­нее слагаемое (e/c)Av, линейное по скорости, не является ни кинетической, ни потенциальной энергией. Обобщённый им­пульс

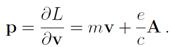
Известно, что поля Е и B, а следовательно, и уравнения движения частиц в электромагнитном поле не изменяются при градиентном преобразовании потенциалов, т. е. при за­мене

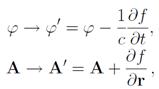
где f — произвольная функция координат и времени. В лагранжевом же формализме это приводит к тому, что по­тенциалам φ', A' и φ, A соответствуют лагранжианы L и L', отличающиеся на полную производную по времени от функции ef/c:

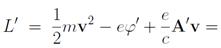
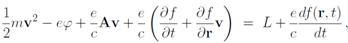
и эти лагранжианы должны быть физически эквивалентны.

Движение заряженной частицы в электромагнитном поле в формализме Гамильтона

Для нерелятивистской частицы в электромаг­нитном поле

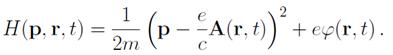
В релятивистском случае

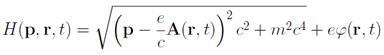
Фотон (квант света) — это релятивистская ча­стица с массой m = 0 и зарядом e = 0. Согласно преды­дущему примеру, его функция Гамильтона для движения в вакууме равна H(p, r) = c|p| .

Распространение света в прозрачной изотропной среде с по­казателем преломления n(r) в приближении геометрической оптики определяется функцией Гамильтона

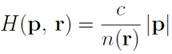
Уравнения Гамильтона имеют вид

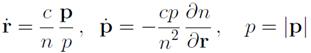
Фактически в геометрической оптике „частицей" является волновой пакет, r(t) есть закон именно его движения, r — это групповая скорость, а вектор р, перпендикулярный к волновому фронту, определяет волновой вектор электромагнитной волны

Определение кин энергии вращающегося твердого тела

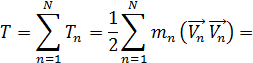
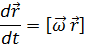
𝜔 – угловая скорость, - расстояние до точки, кот в данный момент вращается

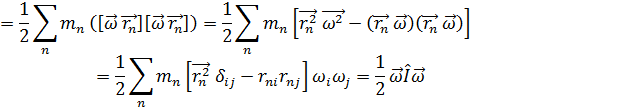
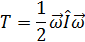
Момент импульса вращения твердого тела.

момент импульса 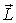тела совпадает по направлению с угловой скоростью 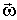тела и определяется формулой

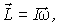где I - момент инерции тела относительно данной главной оси инерции. Причем 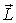не зависит от выбора точки, относительно которой его определяют - при условии, что ось вращения неподвижна.

Найдем выражение для момента импульса твердого тела относительно оси 00'

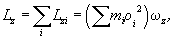
где 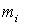и 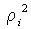- масса и расстояние от оси вращения 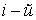частицы твердого тела , 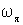- его угловая скорость. Обозначив величину, стоящую в круглых скобках, через I, получим

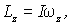где I - так называемый момент инерции твердого тела относительно оси00':

Определение полной производной по времени от векторной физической величины с учётом вращения твёрдого тела.

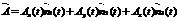
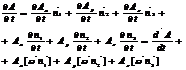
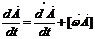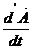, -относительная (локальная) производная. Производная вектора А связана с переносным вращательным движением.