Определение коэффициента вязкости воздуха
Цель работы: вычисление средней длины свободного пробега и эффективного диаметра молекулы азота, который составляет 78,1% воздуха, по коэффициенту внутреннего трения воздуха.
Теоретическая часть
Заметное отклонение молекул от прямолинейных траекторий при тепловом движении происходит только при их достаточном сближении. Такое взаимодействие между молекулами называется столкновением. Процесс столкновения удобно характеризовать величиной эффективного диаметра молекулы. Под ним понимают минимальное расстояние, на которое могут сблизиться центры двух молекул при их столкновении.
Расстояние, которое проходит молекула между двумя последовательными столкновениями, называют длиной свободного пробега молекулы. Из-за хаотичности движения молекул длина свободного пробега изменяется от столкновения к столкновению, поэтому на практике важно знать среднюю длину свободного пробега молекул 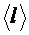 .
.
Молекулярно-кинетическая теория позволила получить формулы, в которых макроскопические параметры газа связаны с его микропараметрами. Пользуясь этими формулами, можно при помощи легко измеримых макропараметров (давление, температура, коэффициент внутреннего трения) получить интересующие нас микропараметры (размер молекулы, среднюю длину ее свободного пробега).
Молекулярно-кинетическая теория устанавливает связь между средней длиной свободного пробега 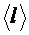 , эффективным диаметром молекул d и концентрацией молекул в газе n:
, эффективным диаметром молекул d и концентрацией молекул в газе n:
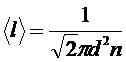 . (1)
. (1)
Внутреннее трение (вязкость) газа характеризуется коэффициентом вязкости 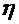 , который зависит от плотности газа
, который зависит от плотности газа 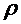 , средней скорости молекул
, средней скорости молекул 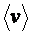 и средней длины свободного пробега
и средней длины свободного пробега 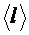 следующим образом:
следующим образом:
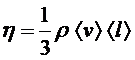 . (2)
. (2)
Средняя скорость молекул идеального газа может быть вычислена из закона распределения Максвелла:
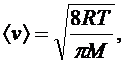 (3)
(3)
где R- универсальная газовая постоянная, T- температура, M- молярная масса газа.
Плотность газа ( 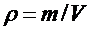 ) можно определить, используя уравнение Менделеева-Клапейрона:
) можно определить, используя уравнение Менделеева-Клапейрона:
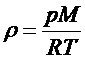 , (4)
, (4)
где p- давление газа. Из формул (2), (3) и (4) получим:
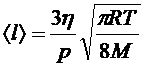 . (5)
. (5)
Если в эксперименте измерить коэффициент вязкости воздуха 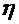 , то по формуле (5) легко вычислить среднюю длину свободного пробега молекул
, то по формуле (5) легко вычислить среднюю длину свободного пробега молекул 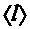 , а затем при помощи формулы (1) вычислить эффективный диаметр молекулы
, а затем при помощи формулы (1) вычислить эффективный диаметр молекулы 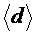 , предварительно выразив концентрацию из формулы:
, предварительно выразив концентрацию из формулы:
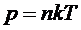 , (6)
, (6)
где 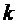 - постоянная Больцмана (
- постоянная Больцмана ( 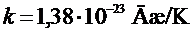 ).
).
Из формул (1), (5) и (6) получим:
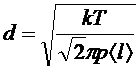 . (7)
. (7)
При ламинарном протекании газа (или жидкости) через цилиндрическую трубку длиной 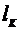 и диаметром
и диаметром 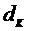 объем газа V, протекающего за время
объем газа V, протекающего за время 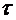 , зависит от вязкости. Эта зависимость выражается формулой Пуазейля[2]:
, зависит от вязкости. Эта зависимость выражается формулой Пуазейля[2]:
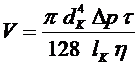 , (8)
, (8)
где 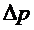 - разность давлений на концах трубки. В данной работе измеряются V,
- разность давлений на концах трубки. В данной работе измеряются V, 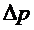 , τ и из формулы (8) определяется
, τ и из формулы (8) определяется 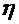 .
.
Экспериментальная часть
Описание установки
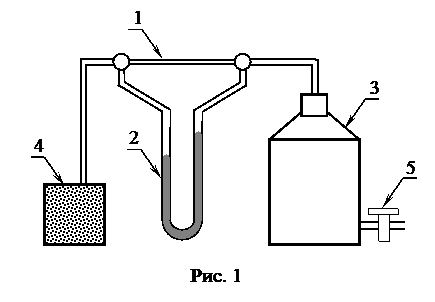
Для определения коэффициента внутреннего трения воздуха используется установка, внешний вид которой показан на рис. 1. Капилляр (1) длиной 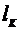 и диаметром
и диаметром 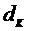 , к концам которого подключен манометр (2), соединен одним концом с аспиратором (3), а другим с осушителем (4). Когда из аспиратора выливается вода, давление в нем понижается, и через капилляр течет воздух, который засасывается через осушительный фильтр (4) с
, к концам которого подключен манометр (2), соединен одним концом с аспиратором (3), а другим с осушителем (4). Когда из аспиратора выливается вода, давление в нем понижается, и через капилляр течет воздух, который засасывается через осушительный фильтр (4) с 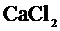 . Вследствие внутреннего трения давления на концах капилляра неодинаковы. Разность этих давлении
. Вследствие внутреннего трения давления на концах капилляра неодинаковы. Разность этих давлении 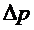 измеряется манометром. Объем
измеряется манометром. Объем 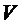 воздуха, прошедшего за время
воздуха, прошедшего за время 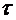 через капилляр, равен объему вытекшей из аспиратора воды и определяется по его шкале в литрах.
через капилляр, равен объему вытекшей из аспиратора воды и определяется по его шкале в литрах.
Выполнение работы
1. Заполнить аспиратор водой так, чтобы ее уровень был выше нулевого деления шкалы аспиратора.
2. Открыть кран (5) и выждать некоторое время, пока установится стационарное течение (при этом разность уровней жидкости в манометре будет постоянной). Записать эту разность уровней 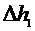 (это и последующие значения заносятся в таблицу).
(это и последующие значения заносятся в таблицу).
| № | 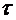 , с , с | 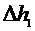 , м , м | 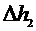 , м , м | 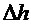 , м , м | 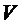 , м3 , м3 | 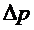 , Па , Па | 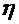 , Па·с , Па·с |
| 1. | |||||||
| 2. | |||||||
| 3. | |||||||
| 4. | |||||||
| 5. |
3. Когда уровень воды достигнет нулевого деления на шкале аспиратора, включить секундомер. После того как вытечет объем воды 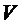 (значение задает преподаватель), выключить секундомер (кран (5) не закрывать) и вновь записать разность уровней жидкости в манометре
(значение задает преподаватель), выключить секундомер (кран (5) не закрывать) и вновь записать разность уровней жидкости в манометре 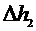 . Теперь закрыть кран (5).Записать показание секундомера. Опыт повторить пять раз.
. Теперь закрыть кран (5).Записать показание секундомера. Опыт повторить пять раз.
4. Для нахождения разности давлений на концах капилляра следует воспользоваться известной формулой 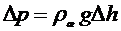 , где
, где 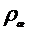 - плотность жидкости в манометре (жидкость, используемая в манометре, указана на установке),
- плотность жидкости в манометре (жидкость, используемая в манометре, указана на установке), 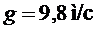 - ускорение свободного падения,
- ускорение свободного падения, 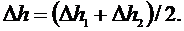
5. Вычислить вязкость воздуха 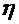 для пяти измерений и среднее значение вязкости воздуха
для пяти измерений и среднее значение вязкости воздуха 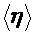 . Длина капилляра
. Длина капилляра 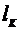 и его диаметр
и его диаметр 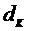 указаны на установке.
указаны на установке.
6. По приборам лаборатории определить температуру воздуха в комнате и атмосферное давление.
7. Вычислить, используя ранее рассчитанное значение 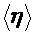 , среднюю длину свободного пробега
, среднюю длину свободного пробега 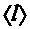 и эффективный диаметр
и эффективный диаметр 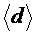 молекулы азота.
молекулы азота.
8. Рассчитайте абсолютную 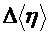 и относительную
и относительную 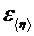 погрешности определения вязкости воздуха, запишите окончательный результат.
погрешности определения вязкости воздуха, запишите окончательный результат.
9. Сравните полученные результаты 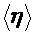 ,
, 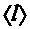 и
и 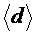 с табличными значениями.
с табличными значениями.
Контрольные вопросы
1. Что называют средней длиной свободного пробега и эффективным диаметром молекул газа?
2. Объяснить молекулярно-кинетический механизм вязкости газов.
3. Как зависят средняя длина свободного пробега и эффективный диаметр молекул газа от температуры?
Литература
1. Лабораторный практикум по физике/Под ред. Ахматова Д.С, М.: 1980.
2. Сивухин Д.В. Общий курс физики. Термодинамика и молекулярная физика. М.: Наука, 1979.
3. Кикоин И.К., Кикоин А.К. Молекулярная физика. М.: 1963.
4. Физические величины: Справочник / Под ред. И. К. Кикоина.- М.: Атомиздат, 1976.
Лабораторная работа № 5
