Работа газа при изменении его объема
Первое начало термодинамики
Рассмотрим термодинамическую систему (газ), внутренняя энергия которой U изменяется за счет совершения над системой работы A и за счет сообщения ей некоторого количества теплоты Q.
Первое начало термодинамики утверждает (на основе обобщения многовековых опытных данных), что
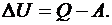 (6.5)
(6.5)
Формулу (6.5) можно переписать в виде
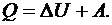 (6.6)
(6.6)
теплота, сообщенная системе, расходуется на увеличение ее внутренней энергии и на совершение работы против внешних сил. Для малых изменений системы имеем
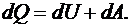 (6.7)
(6.7)
Если термодинамическая система периодически возвращается в исходное состояние, то изменение внутренней энергии равно нулю ( 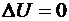 ), и вся подведенная к системе теплота может быть, согласно первому началу термодинамики, переведена в работу
), и вся подведенная к системе теплота может быть, согласно первому началу термодинамики, переведена в работу 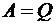 . Причем, нельзя построить периодически действующий двигатель, который совершал бы работу, большую, чем количество сообщающейся ему извне энергии, или невозможен вечный двигатель 1-го рода.
. Причем, нельзя построить периодически действующий двигатель, который совершал бы работу, большую, чем количество сообщающейся ему извне энергии, или невозможен вечный двигатель 1-го рода.
Первое начало термодинамики – это закон сохранения энергии в термодинамике.
Работа газа при изменении его объема
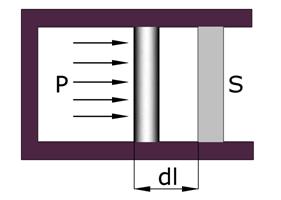
Рассмотрим газ, находящийся под поршнем в цилиндрическом сосуде.
Газ, расширяясь, передвигает поршень на расстояние dl и производит работу
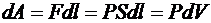 (6.8)
(6.8)
где 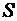 – площадь поршня;
– площадь поршня; 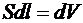 – изменение объема.
– изменение объема.
Таким образом, работа при расширении газа определяется как
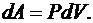 (6.9)
(6.9)
 | Работа в процессе 1–2 может быть найдена интегрированием формулы (6.9). При этом необходимо учитывать зависимость 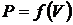 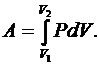 (6.10) (6.10) |
| Рис. 6.2 |
При расширении газа 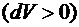 работа положительна
работа положительна 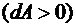 , то есть газ совершает работу, при сжатии
, то есть газ совершает работу, при сжатии 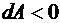 , т. е. работа совершается над газом.
, т. е. работа совершается над газом.
Адиабатический процесс
Адиабатическим называется процесс, при котором отсутствует теплообмен между термодинамической системой и окружающей средой 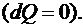
Из первого начала следует, что
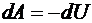 (6.29)
(6.29)
или
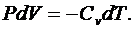 (6.30)
(6.30)
Найдем уравнение, связывающее параметры состояния в адиабатном процессе. Для этого продифференцируем уравнение состояния для 1 моля газа
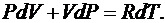 (6.31)
(6.31)
Разделив уравнение (6.31) на выражение (6.30), получим
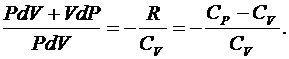 (6.32)
(6.32)
Разделим переменные, тогда с учётом 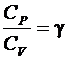 выражение (6.32) примет вид
выражение (6.32) примет вид
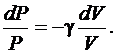 (6.33)
(6.33)
Интегрируя (6.32) в пределах от Р1 до Р2 и от V1 до V2, получим
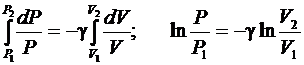 ; (6.34)
; (6.34)
или
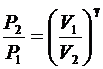 или
или 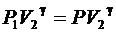 (6.35)
(6.35)
Так как состояния 1 и 2 выбраны произвольно, то (6.35) можно записать:
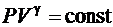 (6.36)
(6.36)
Уравнение (6.36) называется уравнением Пуассона, которое описывает адиабатический процесс. Используя уравнения Клапейрона – Менделеева, можно записать уравнение Пуассона в виде
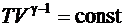 (6.37)
(6.37)
или
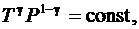 (6.38)
(6.38)
где g – коэффициент Пуассона, равный 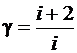 ; при i = 3g = 1,67, при i = 5, g = 1,4.
; при i = 3g = 1,67, при i = 5, g = 1,4.
График адиабаты представлен на рис. 6.5. Адиабата более крута, чем изотерма. Это объясняется тем, что увеличение давления газа обусловлено не только уменьшением объема как при изотермическом сжатии, но и повышением температуры. При адиабатическом процессе изменяются все три параметра P, V и T .
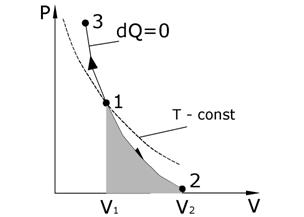 | Вычислим работу, совершаемую газом при адиабатическом процессе: 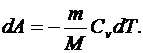 (6.39) Интегрируя выражение (6.39), получим (6.39) Интегрируя выражение (6.39), получим |
| Рис.6.5 |
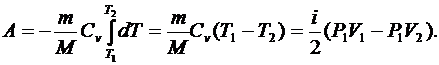 (6.40)
(6.40)
Работа, совершаемая газом при адиабатическом процессе, численно равная заштрихованной площади на рис. 6.5, меньше, чем при изотермическом процессе.
Политропный процесс
Все рассмотренные выше процессы обладают одной общей особенностью – они происходят при постоянной теплоемкости С
при 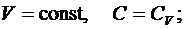
при 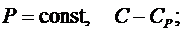 (6.41)
(6.41)
при 
при 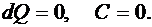
Процессы, в которых теплоемкость постоянна, называют политропными. Все изопроцессы, включая адиабатический, являются частными случаями политропного процесса.
Аналогично выводу уравнения адиабаты (6.37), используя первое начало термодинамики и уравнение Менделеева – Клапейрона для 1 моля,

получим
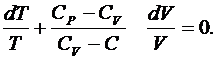 (6.42)
(6.42)
Интегрируя выражение (6.42), получим уравнение политропы
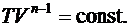 (6.43)
(6.43)
Заменив в (6.43) температуру T соотношением, полученным из уравнения Менделеева – Клапейрона, как 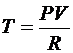 , получим
, получим
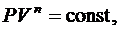 (6.44)
(6.44)
где 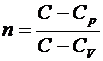 – показатель политропы.
– показатель политропы.
При 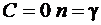 получим
получим 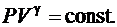
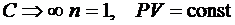 – уравнение изотермы;
– уравнение изотермы;
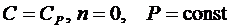 – уравнение изобары; (6.45)
– уравнение изобары; (6.45)
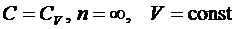 – уравнение изохоры.
– уравнение изохоры.
Цикл Карно и его КПД
Карно рассмотрел работу идеальной тепловой машины, обладающей наибольшим коэффициентом полезного действия  .
.
В основе цикла Карно лежит круговой процесс, представленный на рис. 6.8, состоящий из двух изотерм (1–2 и 3–4) и двух адиабат (2–3 и 4–1). В качестве рабочего тела используется один моль идеального газа, заключенный в сосуд с подвижным поршнем.
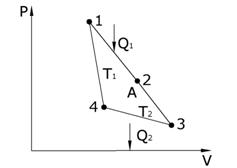 | Работа на участке 1–2 (T = const) количество тепла, полученное газом от нагревателя 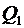 , равно работе расширения газа , равно работе расширения газа 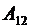 , которая определяется как , которая определяется как |
| Рис. 6.8. |
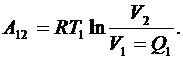 (6.47)
(6.47)
При адиабатическом расширении газа (участок 2–3) работа равна:
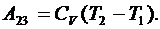 (6.48)
(6.48)
Количество теплоты 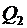 , отданное газом холодильнику, при изотермическом сжатии (участок 2–3), равно работе сжатия А34:
, отданное газом холодильнику, при изотермическом сжатии (участок 2–3), равно работе сжатия А34:
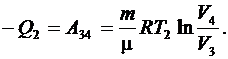 (6.49)
(6.49)
На участке 4–1 работа адиабатического сжатия определяется как
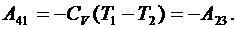 (6.50)
(6.50)
Таким образом, работа за цикл 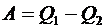 , так как
, так как  и определяется площадью кругового процесса на рис. 6. 8.
и определяется площадью кругового процесса на рис. 6. 8.
Коэффициент полезного действия цикла согласно формуле (6.46) равен
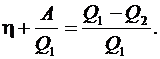 (6.51)
(6.51)
Из уравнений адиабат следует, что
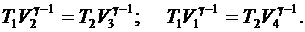
Откуда
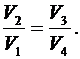 (6.52)
(6.52)
Подставив выражения (6.47) и (6.49) для 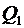 и
и 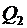 в формулу (6.52), получим
в формулу (6.52), получим
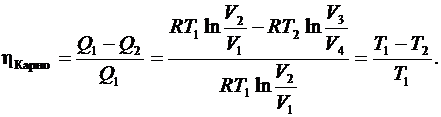 (6.53)
(6.53)
Формула (6.53) была получена Клаузиусом. КПД цикла Карно определяется только температурой нагревателя и холодильника
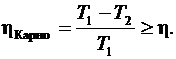 (6.54)
(6.54)
Таким образом, идеальная тепловая машина, работающая по обратимому циклу Карно, имеет наибольший КПД, определяемый температурой нагревателя Т1 и холодильника Т2, не зависящий от конструкции машины.
Энтропия
Понятие энтропии введено Клаузиусом. Коэффициент полезного действия реальной тепловой машины всегда меньше h идеальной машины, т. е.
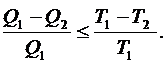 (6.55)
(6.55)
Выражение (6.55) можно записать в следующем виде
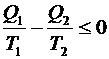 – неравенство Клаузиуса, (6.56)
– неравенство Клаузиуса, (6.56)
где 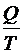 – приведенная теплота; знак «–» учитывает, что на каком-то участке цикла тепло отдается.
– приведенная теплота; знак «–» учитывает, что на каком-то участке цикла тепло отдается.
Из неравенства Клаузиуса следует, что для обратимого цикла алгебраическая сумма приведенной теплоты равна нулю.
Если разбить весь обратимый цикл Карно на бесконечно малые циклы, то для каждого из них можно записать
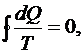 (6.57)
(6.57)
где 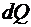 – бесконечно малое количество теплоты, переданное (отнятое) телу при температуре Т.
– бесконечно малое количество теплоты, переданное (отнятое) телу при температуре Т.
Из (6.57) следует, что 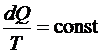 и является функцией состояния, которую Клаузиус назвал энтропией S, что по-гречески означает «превращение», т. е.
и является функцией состояния, которую Клаузиус назвал энтропией S, что по-гречески означает «превращение», т. е.
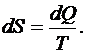 (6.58)
(6.58)
Изменение энтропии не зависит от пути перехода из одного состояния в другое, а определяется состоянием системы.
II начало термодинамики можно сформулировать, используя понятие энтропии. Если в изолированной системе происходят только обратимые процессы, то ее энтропия остается постоянной, т. е.
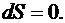 (6.59)
(6.59)
И, наоборот, при необратимых процессах энтропия в изолированной системе возрастает
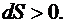 (6.60)
(6.60)
В открытой системе энтропия может как возрастать, так и убывать, или оставаться неизменной.
Уравнение Ван-дер-Ваальса
В отличие от идеальных, в реальных газах учитываются силы взаимодействия между молекулами и их объем. Из большого числа уравнений, предложенных для описания реальных газов, наиболее простым и вместе с тем дающим достаточно хорошие результаты признано уравнение голландского физика Ван-дер-Ваальса.
Ван-дер-Ваальс ввел две поправки в уравнение Менделеева – Клапейрона, учитывающие собственный объем молекул и силы межмолекулярного взаимодействия.
Из-за действия сил отталкивания молекулы не могут сблизиться на расстояние < d, то есть свободный объем, доступный молекулам одного моля реального газа будет не 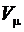 , а
, а 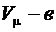 ( где в – объем, занимаемый молекулами).
( где в – объем, занимаемый молекулами).
Действие сил притяжения приводит к появлению дополнительного давления на газ, называемого внутренним давлением Р'. По расчетам Ван-дер-Ваальса внутреннее давление определяется как:
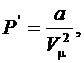 (6.63)
(6.63)
где а – постоянная Ван-дер-Ваальса; 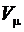 – объем одного моля газа.
– объем одного моля газа.
Вводя приведенные выше поправки в уравнения Менделеева–Клапейрона 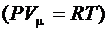 , получим уравнение Ван-дер-Ваальса для одного моля газа:
, получим уравнение Ван-дер-Ваальса для одного моля газа:
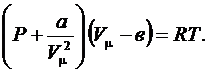 (6.64)
(6.64)
Для произвольной массы газа с учетом того, что 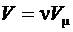 уравнение состояния реального газа (Ван-дер-Ваальса), примет вид:
уравнение состояния реального газа (Ван-дер-Ваальса), примет вид:
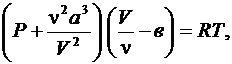 (6.65)
(6.65)
где 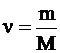 – число молей газа; a и в – поправки Ван-дер-Ваальса, постоянные для каждого газа и определяются опытным путем.
– число молей газа; a и в – поправки Ван-дер-Ваальса, постоянные для каждого газа и определяются опытным путем.
Так как 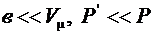 , то при малых давлениях и высоких температурах уравнение Ван-дер-Ваальса совпадает с уравнением Клапейрона – Менделеева.
, то при малых давлениях и высоких температурах уравнение Ван-дер-Ваальса совпадает с уравнением Клапейрона – Менделеева.
Первое начало термодинамики
Рассмотрим термодинамическую систему (газ), внутренняя энергия которой U изменяется за счет совершения над системой работы A и за счет сообщения ей некоторого количества теплоты Q.
Первое начало термодинамики утверждает (на основе обобщения многовековых опытных данных), что
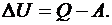 (6.5)
(6.5)
Формулу (6.5) можно переписать в виде
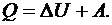 (6.6)
(6.6)
теплота, сообщенная системе, расходуется на увеличение ее внутренней энергии и на совершение работы против внешних сил. Для малых изменений системы имеем
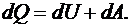 (6.7)
(6.7)
Если термодинамическая система периодически возвращается в исходное состояние, то изменение внутренней энергии равно нулю ( 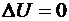 ), и вся подведенная к системе теплота может быть, согласно первому началу термодинамики, переведена в работу
), и вся подведенная к системе теплота может быть, согласно первому началу термодинамики, переведена в работу 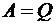 . Причем, нельзя построить периодически действующий двигатель, который совершал бы работу, большую, чем количество сообщающейся ему извне энергии, или невозможен вечный двигатель 1-го рода.
. Причем, нельзя построить периодически действующий двигатель, который совершал бы работу, большую, чем количество сообщающейся ему извне энергии, или невозможен вечный двигатель 1-го рода.
Первое начало термодинамики – это закон сохранения энергии в термодинамике.
Работа газа при изменении его объема
Рассмотрим газ, находящийся под поршнем в цилиндрическом сосуде.
Газ, расширяясь, передвигает поршень на расстояние dl и производит работу
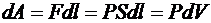 (6.8)
(6.8)
где 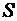 – площадь поршня;
– площадь поршня; 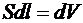 – изменение объема.
– изменение объема.
Таким образом, работа при расширении газа определяется как
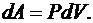 (6.9)
(6.9)
 | Работа в процессе 1–2 может быть найдена интегрированием формулы (6.9). При этом необходимо учитывать зависимость 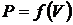 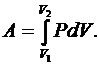 (6.10) (6.10) |
| Рис. 6.2 |
При расширении газа 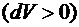 работа положительна
работа положительна 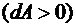 , то есть газ совершает работу, при сжатии
, то есть газ совершает работу, при сжатии 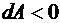 , т. е. работа совершается над газом.
, т. е. работа совершается над газом.
