Методические указания к выполнению контрольной работы № 2
В контрольную работу № 2 включены задачи на темы: уравнение состояния идеального газа; основное уравнение молекулярно-кинетической теории газов, внутренняя энергия идеального газа; элементы классической статистики; первое начало термодинамики, теплоёмкость идеальных газов; циклы, КПД цикла, цикл Карно; энтропия термодинамических систем.
При решении задач необходимо выполнить общие методические рекомендации.
Задачи 201...220 относятся к теме “Идеальный газ. Уравнение состояния идеального газа”. Решение этих задач требует усвоения основных понятий: моль, молярная масса, параметры состояния (р,V, Т), уравнение состояния.Следует выяснить, какой именно процесс рассматривается в конкретной задаче.
Для решения этих задач необходимо проработать материал по учебному пособию [1], с. 81...87.
Задачи 221...230 относятся к теме “Основное уравнение молекулярно-кинетической теории газов. Внутренняя энергия идеального газа”.Здесь необходимо усвоить понятие числа степеней свободы молекул газа, понимать, какое число степеней свободы описывает движение молекул одноатомного, двухатомного и многоатомных газов, усвоить смысл основного уравнения молекулярно-кинетической теории.
Предварительно проработайте этот материал по учебному пособию [1], с. 100...101.
Задачи 231...240 на тему “Элементы классической статистики” посвящены расчёту средней квадратичной, средней и наиболее вероятной скоростей, длины свободного пробега молекул. Для решения этих задач проработайте данную тему по учебному пособию [1], с. 87...93.
Задачи 241...260 относятся к теме “Первое начало термодинамики. Теплоёмкость идеальных газов”.В задачах 241...250 рассматривается применение первого начала термодинамики к изопроцессам и адиабатному процессу.Задачи 251...260 посвящены вычислению теплоёмкости идеального газа при постоянном давлении СP и постоянном объеме СV.
Приступая к решению задач ознакомьтесь с данной темой по учебному пособию [1], с. 101...103; 105...109.
Задачи 261...270 посвящены изучению циклических процессов, вычислению работы цикла, КПД цикла, работы расширения и сжатия газа, определению КПД идеальной тепловой машины, работающей по циклу Карно.
Перед решением задач проработайте эту тему по учебному пособию [1], с. 110-111; 115...118.
Вычислению изменения энтропии в различных процессах посвящено решение задач 271...280. Проработайте теоретический материал по теме “Энтропия” по учебному пособию [1], с. 111...114.
Перед выполнением контрольной работы полезно, ознакомиться с основными законами и формулами, а также справочными материалами, приведёнными в приложениях. После этого надо разобрать примеры решения типовых задач из данной методической разработки и уже затем приступать к решению контрольной работы.
Табл. 2
| Вариант | Номера задач | |||||||
Основные законы и формулы. Примеры решения задач
3.2.1. Идеальный газ. Уравнение состояния идеального газа (уравнение Клапейрона-Менделеева)
1. Уравнение Клапейрона-Менделеева
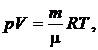
где р – давление газа;V – его объем;T – термодинамическаятемпература;m – масса газа;m – молярная масса;R – универсальная газовая постоянная;R=8,31 Дж/(моль К);m/m – количество вещества.
2. Количество вещества (в моль)
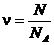 или
или 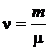 ,
,
где N – число молекул в данной массе газа;NA = 6,02.1023 моль-1 – число Авогадро (число молекул в одном моле).
3. Объединённый газовый закон
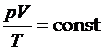 .
.
В случае двух состояний
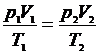 ,
,
где р1, V1, Т1 – параметры, определяющие начальное состояние; р2, V2, Т2 – параметры, определяющие конечное состояние.
4. Уравнение состояния изотермического процесса
рV = const при Т = cоnst
5. Уравнение состояния изобарного процесса (р = cоnst)
 или
или 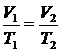 .
.
6. Уравнение состояния изохорного процесса (V = cоnst)
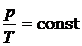 ,
,
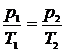 .
.
7. Плотность вещества
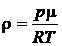 .
.
8. Закон Дальтона. Давление р смеси различных газов равно сумме парциальных давлений газов, составляющих смесь:
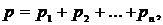
Примеры решения задач
Задача 1
Определить молярную массу смеси газов, состоящую из 25 г кислорода и 75 г азота.
| Дано: | Решение: |
m1 = 25 г = 2,5.10-2 кг 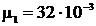 кг/моль m2 = 75 г = кг/моль m2 = 75 г = 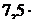 10-2 кг 10-2 кг 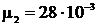 кг/моль кг/моль | Молярная масса смеси 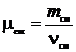 , (1) где масса смеси газов mсм = m1 +m2, (2) , (1) где масса смеси газов mсм = m1 +m2, (2) |
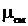 - ? - ? |
где 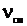 – количество вещества смеси газов
– количество вещества смеси газов
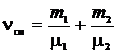 . (3)
. (3)
Подставив выражения (2) и (3) в равенство (1), получим формулу для вычисления молярной массы смеси:
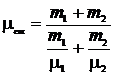 .(4)
.(4)
Проведём вычисления  , подставив числовые значения в формулу (4)
, подставив числовые значения в формулу (4)
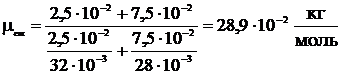 .
.
Задача 2
Азот массой 7 г находится под давлением 0,1 МПа и температуре 290 К. Вследствие изобарного нагревания азот занял объем 10 л. Определить: 1) объем газа до расширения; 2) температуру газа после расширения; плотность газа до и после расширения.
| Дано: | Решение: |
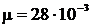 кг/моль m= 7 г = 7.10-3 кг р = 0,1 МПа = 105 Па Т1 = 290 К V2 = 10 л = 10-2 м3 R = 8,31 Дж/ кг/моль m= 7 г = 7.10-3 кг р = 0,1 МПа = 105 Па Т1 = 290 К V2 = 10 л = 10-2 м3 R = 8,31 Дж/ 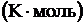 | Для решения задачи воспользуемся уравнением Клапейрона-Менделеева. Запишем его для начального и конечного состояния газа: 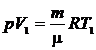 , (1) , (1) 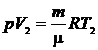 . (2) Из уравнения (1) можно определить . (2) Из уравнения (1) можно определить 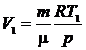 , (3) из уравнения (2) , (3) из уравнения (2) |
1) V1 - ? 2) Т2 - ? 3) 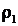 - ? 4) - ? 4) 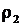 - ? - ? |
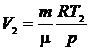 . (4)
. (4)
Из уравнения состояния изобарного процесса: 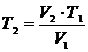 .
.
Плотность газа до расширения
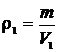 , (5)
, (5)
а после расширения
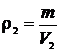 .(6)
.(6)
Проведём вычисления требуемых величин по формулам (3), (4), (5) и (6), подставив в них числовые значения исходных данных, получим:
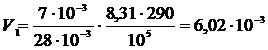 м3.
м3.
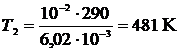 .
.
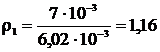 кг/м3.
кг/м3.
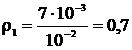 кг/м3.
кг/м3.
