ОПРЕДЕЛЕНИЕ ОТНОШЕНИЯ МОЛЯРНЫХ ТЕПЛОЕМКОСТЕЙ ВОЗДУХА МЕТОДОМ КЛЕМАНА – ДЕЗОРМА

Цель работы:определить 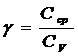для воздуха.

Приборы и принадлежности: прибор Клемана - Дезорма, насос, манометр.

ВВЕДЕНИЕ

Для характеристики тепловых свойств тел в термодинамике широко используют понятие теплоемкости. Теплоемкостью тела называют отношение количества сообщенной ему теплоты DQ к соответствующему изменению температуры тела DТ. Эксперименты и расчеты показывают, что теплоемкость тела зависит от его химического состава, массы и термодинамического состояния, а также от вида процесса изменения состояния тела при сообщении ему теплоты.

Для однородных тел удобно пользоваться удельной и молярной теплоемкостями. Удельной теплоемкостью называют физическую величину С, численно равную количеству теплоты, которое необходимо сообщить единице массы вещества для изменения его температуры на 1К, в рассматриваемом термодинамическом процессе.

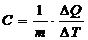(1)

Удельная теплоемкость вещества не зависит от массы вещества, содержащегося в теле. В системе СИ удельная теплоемкость измеряется в джоулях деленных на килограмм – кельвин, что обозначается сокращенно Дж/кгК.

Молярной теплоемкостью называют физическую величину С_m , численно равную количеству теплоты, которую необходимо сообщить одному молю вещества для изменения его температуры на 1К в рассматриваемом термодинамическом процессе. Очевидно, что

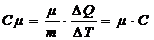(2)

где m - молярная масса вещества,

С – удельная теплоемкость

Для газов надо учитывать, при каких условиях они нагреваются. Различают теплоемкость газов при постоянном давлении и при постоянном объеме. Нагревание газа при постоянном объеме (изохорический процесс) приводи к тому, что все тепло идет на увеличение внутренней энергии газа. В этом случае работа не совершается. Из первого закона термодинамики следует что,

DU=DQ (3)

Учитывая, что внутренняя энергия одного моля газа равна

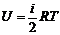(4)

и используя уравнение (2), получим после преобразования

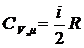(5)

где I – число свободы молекул газа,

R – универсальная газовая постоянная, R=8,31Дж/(мольК)

При нагревании газа при постоянном давлении (изобарический процесс) газ расширяется; сообщаемое ему извне тепло идет не только на увеличение запаса его внутренней энергии DU, но и на совершение работы против внешних сил DА. Таким образом, теплоемкость при постоянном давлении С_Рm больше теплоемкости при постоянном объеме С_V,m на ту работу DА, которую совершает один моль газа при расширении вследствие нагревания его на 1 К при Р=const. Известно, что при этих условиях DА=R, отсюда

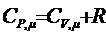(6)

подставив в (6) уравнение (5), получим

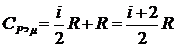(7)

Пользуясь соотношением (2) между удельными и молярными теплоемкостями, находим для удельных теплоемкосте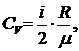й

и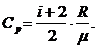

Отношение удельных и молярных теплоемкостей при постоянном давлении и постоянном объеме обозначают g (показатель адиабаты).

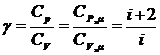(8)

Это отношение зависит только от числа степеней свободы молекул газа. Для одноатомного газа i=3, для двухатомного i=5, для трехатомного и многоатомного i=6.

Отношение теплоемкостей в термодинамике имеет большое значение. Оно входит в уравнение Пуассона, которое описывает адиабатическое расширение газа.

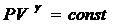(9)

Одним из основных простых методов определения является методом адиабатического расширения. (метод Клемана – Дезорма). В работе определяется g для воздуха (двухатомный газ).

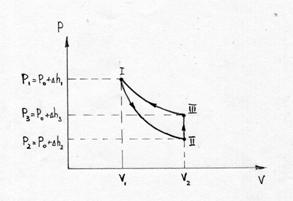
Рисунок 2.

Если от какого – то состояния I (рис. 2.), при котором температура газа в сосуде равна температуре окружающего воздуха Т₁ (3-5 минут давления в сосуде не изменилось), увеличить (или уменьшить объем газа V, то давление, которое было Р₁=Р₀+Dh₁ станет Р₂=Р₀+Dh₂. Если изменение объема происходит достаточно быстро (за 1-2 с.), то теплообмен между газом в сосуде и окружающей средой не успевает произойти и расширение (сжатие) происходит адиабатически, т.е. параметры газа в I и II состояниях связаны уравнением Пуассона:

Р₁V₁^g = Р₂V₂^g или 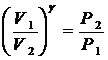(10)

Вследствии теплообмена с окружающей средой температура газа с сосуде ставшая Т₁, а давление станет Р₃.

Параметры газа в состояниях с одинаковыми температуры связаны уравнением Бойля – Мариотта (см. рис. 8.2.) кривая III и II – изотерма.

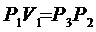т.е.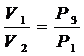

Возведя обе части в степень g получим

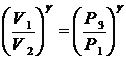(11)

Из (10) и (11) получаем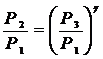

Логарифмируя и решая относительно g получим

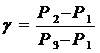
Учитывая, что Р₁, Р₂ и Р₃ мало отличаются друг от друга, можно записать

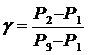
Или, учитывая, что

; ;

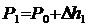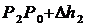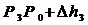
можем записать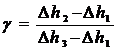

Таким образом, измеряя Dh₁, Dh₂ и Dh₃ – разность уровней воды в манометре, соответствующие начальному состоянию - Dh₁, быстрому расширению - Dh₂ (сжатию) и спустя 3-5 минут после расширения - Dh₃ (сжатия), можно рассчитать значение g.