Критические явления. Теория Ван-дер-Ваальса.

Теперь обратимся к диаграмме PV, являющейся проекцией трёхмерной диаграммы для воды на плоскости P-V при любой температуре.

При достаточно низких температурах любой газ можно превратить в жидкость , приложив внешнее давление: , молекулы сближаются, силы притяжения достаточны, чтобы вызвать конденсацию.

Критерий критического состояния для чистого вещества:

Критическому состоянию соответствует T и P при которых газообразная и жидкая фазы становятся настолько близкими по свойствам, что не могут существовать как отдельные фазы (применимо и к смесям).

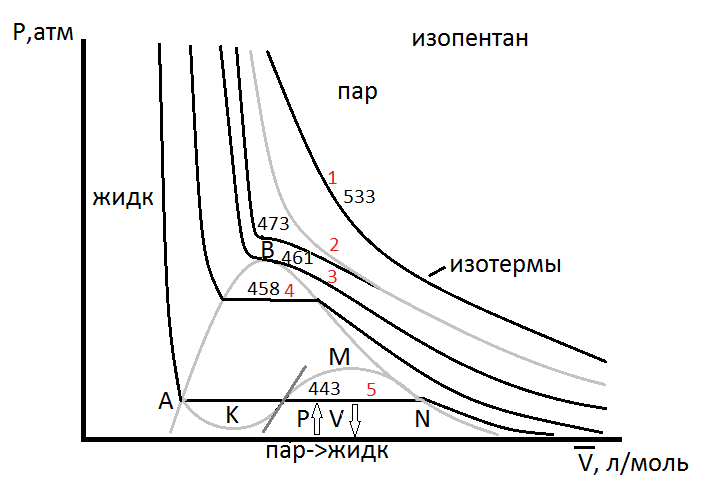
На рисунке показан характер кривых P-V вблизи критической температуры. График изображает зависимость давления пара изопентана от мольного объёма при нескольких температурах.

На рисунке представлены изотермы.

Кривые, соответствующие высоким температурам (>503K) – гиперболы - полная аналогия с идеальными газом. (1)

Кривая при T=473K(2), свидетельствуют, что молекулы уже притягиваются друг к другу и .

Кривые ниже T=461K (3) имеют горизонтальный участок.

Горизонтальные линии (4 и 5) показывают, что бесконечно малое увеличение давления вызывает сильное уменьшение объёма вследствие превращения газа в жидкость.

На диаграмме отмечены области существования всех фаз.

Поскольку жидкость сжимается труднее чем газ – изотермы для неё идут круче.

Вдоль горизонтальных линий сосуществуют одновременно жидкость и газ (газ в равновесии с жидкостью - пар).

На рисунке отмечена область существования пара и жидкости, охватывающая диапазон нахождения горизонтальных участков изотерм. Давления пара изопентана при любой температуре представлены горизонтальными линиями.

Точки максимума B позволяют определить критическую температуру T_к, V_к, P_к.

(Волнообразную кривую NMLKA рассмотрим позднее).

(Вещество вблизи критической точки вещество сильно рассеивает свет, это явление называют критической опалесценцией)

В 1879 году Ван-дер-Ваальс предложил своё толкование неидеального поведения газов, которое помогло понять и критические явления.

Большую сжимаемость реальных газов он он объяснил взаимным притяжением молекул.

Силы приводящие к конденсации до сих пор называются силами Ван-дер-Ваальса.

Происхождение таких сил было впервые объяснено Лондоном в 1930 г.

Ван-дер-Ваальс ввёл поправку на межмолекулярное притяжение, прибавив к измеряемому давлению в уравнении состояния член 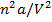, где a – константа Ван-дер-Ваальса, n – число молей газа.

При достаточно высоком давлении реальные газы занимают больший объём, чем идеальные газы. Чтобы учесть это явление Ван-дер-Ваальс ввёл в уравнение состояния действительный объём, в котором движутся молекулы, его получают, вычитая из измеренного объёма V исключаемый объём nb

Полное уравнение Ван-дер-Ваальса:

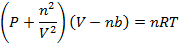
Или

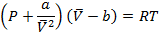
(3.1)

Когда мольный объём велик, b и 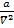становятся пренебрежимо малы. Из уравнения Ван-дер-Ваальса вытекает закон идеального газа .

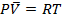Константы можно рассчитать из экспериментально измеренных значений P, 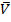, T или из критических констант газа.

Вообще говоря, можно оценить исключаемый объём, допуская, что при достаточно низком давлении молекулы сближаются только попарно, а группы по три молекулы и более можно не принимать во внимание.

Объём, исключаемый для 1 молекулы, можно вычислить если рассматривать молекулы как жесткие сферы.

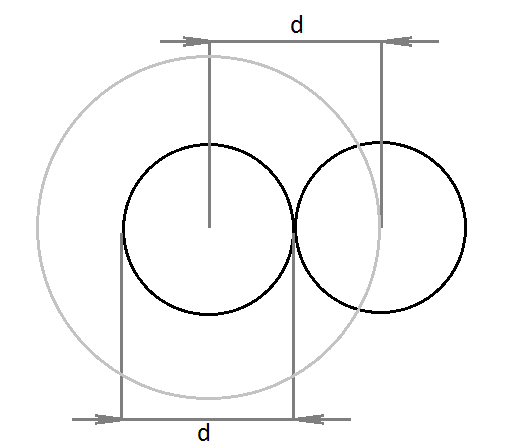Для одной пары исключается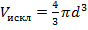

Для одной молекулы -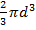

Объём одной молекулы 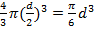, т.е.

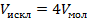
В расчёте на одну молекулу.

В первом приближении константа

b=4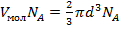

Уравнения Ван-дер-Ваальса в виде

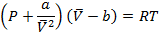
Раскроем скобки и запишем по убывающим степеням :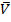

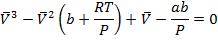
(3.1)’

При T<T_к это уравнение имеет три действительных корня. Графически уравнение может быть представлено в виде волнообразной кривой NMLKA на изотерме 443К.

Точки пересечения N,L,A на горизонтальной линии (P=const) дают три действительных значения .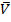

Рассчитанная кривая даёт как бы непрерывный переход из газообразной фазы в жидкость, но такого нет, а есть существование газа и жидкости вдоль горизонтальных прямых.

Теоретическая линия NMLKA не соответствует физическим представлениям.

При критической T_к (461K для пентана) и критическом давлении P_к уравнение (3.1)’ имеет только один действительный корень .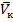

Значение констант a и b в уравнении Ван-дер-Ваальса можно рассчитать из критических констант газа.

Критическая точка – точка перегиба на кривой PV, т.е.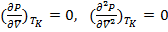

Критические явления наблюдаются для жидких растворов, биополимеров, жидких кристаллов, сплавов, сверхпроводников и ферромагнетиков.