Энтальпия (Тепловая функция)

Процессы, протекающие при постоянном давлении встречаются в физической химии чаще, чем процессы протекающие при при постоянном объеме, т.к. большинство процессов проводится в открытых сосудах.

Если совершается только работа расширения и давление P поддерживается постоянным, то Iзакон термодинамики можно записать в виде

(1.13)

Или U₂-U₁=q-P(V₂-V₁)

Поглощенная теплота равна q=(U₂+PV₂)-(U₁+PV₁)

U+PV – величина являтся функцией состояния

Пусть H=U+PV новая функция состояния энтальпия

(1.14)

Или уравнение (20) -> q=H₂-H₁= H

То есть теплота, поглощенная в процессе, который протекает при постоянном давлении, равна изменению энтальпии, если единственным видом произведенной работы является работа расширения.

Пример:

Пусть совершается только механическая работа в калориметре с постоянным объемом q= U (из I закона), количество выделившейся теплоты есть U, а в калориметре с P=const, количество выделившейся теплоты есть мера уменьшения энтальпии H, q= H.

Теплоёмкость

Определение:

Теплоёмкостью называется количество теплоты, необходимое для того, чтобы повысить Т системы на какую-то определенную величину (обычно на 1⁰), т.е. отношение поглощенной теплоты к приросту T: q/ T

Теплоёмкость при данной Т представляет собой предел к которому стремится это отношение при уменьшении T.

C=

Пусть существует система химически инертная, обладает постоянной массой m и совершает работу расширения.

U=f(T,V) U – функция состояния

Полный дифференциал U:

(1.15)

– изменение внутренней энергии за счет изменения Т

- изменение внутренней энергии за счет изменения V

Поскольку система сама совершает работу (расширение), то

и =>

(1.16)

Т.о. количество поглощенной теплоты зависит не только от прироста T, но и от изменения V.

Пусть V=const: или

(1.17)

- измеряется экспериментально при постоянном объёме.

С другой стороны в такой же системе H – функция(P,T) и

(1.18)

(1.19)

Как соотносятся C_p и C_v?

C_p> C_v, так как нагревание вещества при P=const всегда сопровождается работой расширения.

Поделим 1.16 на dT:

Пусть P=const:

(1.20)

Для одного моля чистого вещества:

(1.21)

{ -мольные C}

Велbчину можно измерить экспериментально

Опыт Джоуля

При открытии крана газ переходит из сосуда 1 в сосуд 2. Такое расширение газа не приводит к заметному изменению Т жидкости, т.е. 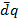=0; При таком расширении никакая работа не совершается =>

Пусть Т=const => dU – полный дифференциал (1.15);

dU= =0

dV≠0 =>

(1.22)

Т.о. внутренняя энергия газа при постоянной Т не зависит от V.

Уравнение 1.22 справедливо для идеальных газов.

Для реальных газов величина ≠0

Учтем также, что T=const

(1.23)

Молекулы идеального газа не взаимодействуют друг с другом => энергия остается неизменной при изменении расстояния между молекулами.

Уравнения 1.22 и 1.23 являются выражениями закона идеальных газов и выводятся из IIЗакона термодинамики, применив закон идеальных газов.

Кроме того учтем для идеальных газов

Тогда разность 1.21 теплоемкостей приобретает вид

(1.24)

Общее выражение для газов будет получено с помощью II закона термодинамики.

Вообще говоря, чем сложнее молекула, тем больше её мольная теплоёмкость и тем больше влияние Т.

Зависимость от Т для пара газов.

Мольную теплоёмкость простых газов можно с большой точностью вычислить метеорологических данных, чем непосредственно измерить в эксперименте, особенно при высоких Т.

Для вычисления теплоты поглощаемой 1 молем при нагревании газа от Т₁ до Т₂, удобно представить как функцию Т.

Эмпирическое уравнение применимо в диапазоне Т 300-1500К

Теплоемкость твердых тел см. ФТТ

особенно полезно для расчета С твердого тела при Т<15К

Примеры:

1)Молекулярные кристаллы, в частности кристаллы инертных газов. Энергия взаимодействия двух частиц может быть представлена

Запишем потенциал в более красивой форме

имеем потенциал Ленарда Джонса.

Этот потенциал описывает свойства газообразных Ne-Xe (атомы не деформируются при объединении в тв. т.)

Параметры подобрать так, чтобы они позволяли хорошо описывать термодинамические свойства газов. А затем использовать те же параметры для описания свойств твердых тел, сопоставив результаты с экспериментом.

2)Ионные кристаллы.

Полная энергия ионного кристалла в состоянии равновесия

(если силы отталкивания )

– равновесное состояние между ионами

постоянная Манделунга

константа, определяемая природой кристалла (справедливость подобного выражения подвергается проверке с помощью термодинамического цикла Габера-Борна)

Рассматривается 1 моль NaCl. Переводится это кол-ва вещества из кристаллического состояния в пар (ионный и атомный) Для вычисления теплоты используем теплоемкость. Зная теплоту реакции можно определить U.

Термохимия

1.10.1 Определения.

В термохимии предметом рассмотрения является теплота, поглощаемая или выделяемая в химических реакциях (1), при разовых превращениях (2) или при разбавлении растворов (3).

Экзотермические реакции протекают с выделением q и

Эндотермические реакции протекают с поглощением q и

Изменение в химических реакциях зависит от того, в каком состоянии находится вещества и продукты реакции.

Например, теплота сгорания графита ≠ теплоте сгорания алмаза.

Значение термодинамических свойств обычно приводятся для стандартных состояний.

Стандартное состояние газа – это идеальный газ при P=1атм и данной Т, стандартное состояние твердого тела – это характерное кристаллическое состояние при P=1атм и данной Т, например, графит для углерода.

Стандартное состояние растворенного вещества – это концентрация, при которой активность = 1.

Температуру следует указать особо, т.к термодинамические функции табулируются при Т=25⁰С.

Термодинамические функции в стандартном состоянии помечаются верхним индексом «⁰».

Уже знаем, что теплота, поглощенная при P=const в реакциях где единственным видом произведенной роботы является работа расширения = , т.е. разности энтальпий продуктов реакции, указных в правой части уравнения, в их конечном состоянии Н₁-Н данного числа молей реагирующих веществ, указанных слева, в их начальном состоянии. Можно определить только изменение Н, но не их абсолютные значения.

Калориметрические изменения

Теплота, выделяемая или поглощаемая в химической реакции измеряется с помощью калориметра. Наиболее распространенный тип калориметра представляет собой камеру, в которой протекает реакция, а камера помещенная в сосуд, заполнена известным количеством воды. Повышение температуры воды измеряется чувствительным термометром произведение (С_воды+С_калор) выделившейся.

С_воды: m_воды*С_уд

С_калор.: в калориметре проводят реакцию с известным тепловым эффектом.

Для термохимических измерений пригодны только реакции, которые проходят быстро и до конца, теплота сгорания в термохимии имеет наибольшее значение.

Сравнение различного типа реакций проводят по величине изменения стандартной энтальпии в данной реакции при 25⁰С 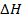⁰.

Колориметрические реакции бывают двух типов:

1) В калориметре с V=const: работа не производится, => поглощается приросту внутренней энергии.

2) В калориметре с P=const: I закон

Количества теплоты , поглощаемые в обоих экспериментах отличаются.

Задача 5

Теплота сгорания СО в калориметре с постоянным объемом равна -67,370 ккал/моль.

Вычислить теплоту сгорания в калориметре с постоянным давлением при допущении, что газы идеальны.

СО(газ)+1/2О₂(газ)=СО₂(газ)

В других типах калориметрических измерений выделяется очень маленькие количества теплоты и поэтому применяют чувствительные дифференциальные методы (термисторы) некоторые специальные калориметры имеют чувствительность в 1 мккал. Такие калориметры можно использовать для измерения теплоты, выделяющейся в реакциях с участием белков и полинуклеидов.

Теплоты сгорания имеют практическое значение, а не только теоретическое.

(Например, для того, чтобы человеку полностью израсходовать энергию, полученную от 1 свиного шницеля нужно 2 часа убирать снег, в то время как 10 минут плавания по энергии эквивалентны 1 яблоку.)

Пример:

1)Покупатель должен знать теплоту сгорания 1г угля.

2)Врач-диетолог должен знать число ккал, получаемое при сгорании различных видов пищи.