Интерпритации уравнения Бернулли
Существует две интерпретации (пояснения) уравнения Бернулли энергетическая и геометрическая (гидравлическая).
Энергетическая интерпретация.
Удельной энергией называется энергия отнесённая к весу частицы жидкости. Энергия положения частицы жидкости равна dm g z, а вес dm g z. тогда
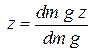 - удельная энергия положения. - удельная энергия положения. |
Энергия давления частицы жидкости равна p dV, тогда
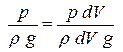 - удельная энергия давления. - удельная энергия давления. |
Кинетическая энергия частицы жидкости равна dm a v2/2, тогда
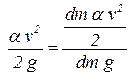 - удельная кинетическая энергия. - удельная кинетическая энергия. |
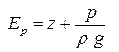 - удельная потенциальная энергия. - удельная потенциальная энергия. |
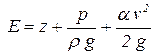 - полная удельная энергия. - полная удельная энергия. |
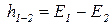 - потеря полной удельной энергии. - потеря полной удельной энергии. |
Тогда в сокращенном виде уравнение можно записать
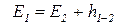 . . |
Геометрическая интерпретация.
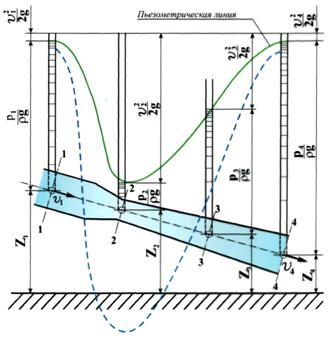
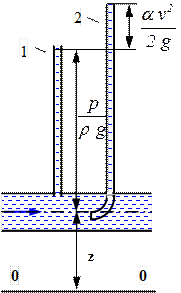 Рисунок 2.11 -– Геометрическая интерпретация уравнения Бернулли. Рисунок 2.11 -– Геометрическая интерпретация уравнения Бернулли. |
Каждое слагаемое в уравнении Бернулли имеет размерность высоты. Рассмотрим трубу, из которой выведены две трубки (рисунок 2.11). Первая трубка называется пьезометром, а вторая (изогнутая навстречу потоку) гидродинамической трубкой или трубкой Пито. Если на оси трубы давление равно p, то уровень жидкости в пьезометре поднимется на высоту hp = p/(rg), которая называется пьезометрической высотой. Уровень жидкости в гидродинамической трубке выше уровня жидкости в пьезометре на величину:
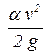 - скоростной напор. - скоростной напор. |
Расстояние от плоскости сравнения до оси трубы z называется геометрическим напором. Остальные слагаемые в Уравнении Бернулли:
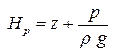 - пьезометрический напор. - пьезометрический напор. |
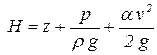 - полный гидродинамический напор. - полный гидродинамический напор. |
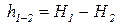 - потеря напора. - потеря напора. |
Поэтому из уравнения Бернулли следует, что для идеальной жидкости полный гидродинамический напор в любом поперечном сечении одинаков и уровень жидкости в гидродинамической трубке будет стоять на одном уровне. Графическое представление уравнения Бернулли называется диаграммой Бернулли и приведено на рисунке 3.12.
Рисунок 2.12 -
- Диаграмма Бернулли |
Примеры и задачи
Пример 2.1.
Идеальный газ движется в сужающейся трубе. Во сколько раз скорость газа в узком сечении больше, чем в широком, если: D1 = 1,5 D2, P1 = 1,2 P2. Движение газа изотермическое.
Решение:
При установившемся движении сжимаемой жидкости сохраняется массовый расход:
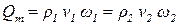 .
.
Найдем отношение скорости в узком (втором) поперечном сечении к скорости в широком поперечном сечении:
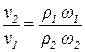 .
.
Так, как движение изотермическое, то плотности газа зависят от давления линейно:
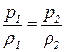 ,
,
Откуда
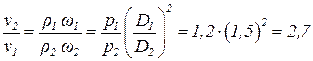
Ответ: скорость газа во втором сечении в 1,8 раза больше, чем в первом.
Пример 2.2.
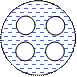 В водо - -водяном теплообменнике жидкость движется в межтрубном пространстве. ВнутреннийВнитренний диаметр корпуса D = 0,2 м, а внешний диаметр каждой из четырёх (n = 4) латунных трубок d = 0,05 м. Определить эквивалентный диаметр для потока и скорость движения жидкости в поперечном сечении (затемненная область), если за 100 секунд прокачивается 1,57 м3 воды.
В водо - -водяном теплообменнике жидкость движется в межтрубном пространстве. ВнутреннийВнитренний диаметр корпуса D = 0,2 м, а внешний диаметр каждой из четырёх (n = 4) латунных трубок d = 0,05 м. Определить эквивалентный диаметр для потока и скорость движения жидкости в поперечном сечении (затемненная область), если за 100 секунд прокачивается 1,57 м3 воды.
Решение:
Площадь поперечного сечения потока равна разности площадейплошадей корпуса и всех латунных трубок:
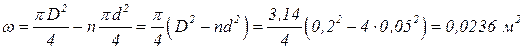 .
.
Смоченный периметр равен сумме периметра корпуса и периметра всех латунных трубок
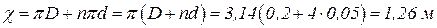
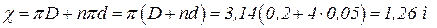 .
.
Тогда эквивалентный диаметр равен четырём гидравлическим радиусам:
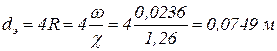
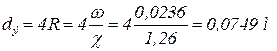 .
.
СкоростьСкороть воды в межтрубном пространстве равна:
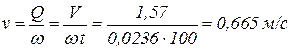
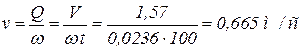 .
.
Ответ: v = 0,665 м/c; dэ = 0,0749 м.
Пример 2.3.
 По трубе диаметром d1 = 0,2 м движется вода. В трех точках производится отбор воды с расходами Q1 = 0,01 м3/с, Q2 = 0,03 м3/с, Q3 = 0,02 м3/с. Определить скорости на участках трубопровода.
По трубе диаметром d1 = 0,2 м движется вода. В трех точках производится отбор воды с расходами Q1 = 0,01 м3/с, Q2 = 0,03 м3/с, Q3 = 0,02 м3/с. Определить скорости на участках трубопровода.
Решение:
Расход на участке от входа в трубопровод до первой точки отбора равен сумме расходов которые отбираются после этого участка:
Qвх-1 = Q1 + Q2 + Q3 = 0,01 + 0,03 +0,02 = 0,06 м3/с.
Тогда скорость на этом участке равна:
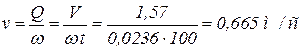
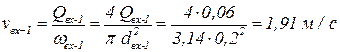 .
.
На участке между первой и второй точками отбора расход равен сумме расходов которые отбираются после этого участка:
Q1-2 = Q2 + Q3 = 0,03 +0,02 = 0,05 м3/с.
Тогда скорость на этом участке равна:
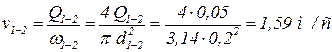 .
.
На участке между второй и третьей точками отбора расход равен:
Q2-3 = Q3 = 0,02 = 0,02 м3/с.
Тогда скорость на этом участке равна:
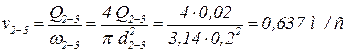 .
.
Ответ: vвх-1 = 1,91 м/c; v1-2 = 1,59 м/c; v2-3 = 0,657 м/c.
 Пример 2.4.
Пример 2.4.
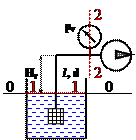
Насос за 10 минут перекачивает 6 м3 воды, по трубе диаметром 100 мм. Высота подъёма жидкости Hг = 4 метра. Потери напора рассчитать по формуле h1-2 = 3 v2/2g, где v – скорость в тубе.
Рассчитать показание вакуумметра.
Решение:
Выберем два поперечных сечения там, где известны давления или где одно из давлений необходимо найти – одно по свободной поверхности жидкости, а второе где стоит вакуумметр.вакууметр. Нумеруем поперечные сечения по направлению движения жидкости в начале потока 1 – 1 в конце 2 – 2 (см. рисунок).
Выбираем плоскость сравнения 0 – 0 проходящую через центр тяжести нижнего поперечного сечения.
Находим значения z и абсолютные давления p в поперечных сечениях:
z1 = 0; p1 = paт; z2 = Нг; p2 = paт – pv.
Расписывают скорости в поперечных сечениях. Площадь поперечного сечения бака большая, поэтому скорость в первом поперечном сечении можно считать равным нулю, а площадь второго поперечного сечения равна площади поперечноготоперечного сечения трубы, поэтомутоэтому скорость во втором сечении равно скорости в трубе:
v1 » 0; v2 = v.
Полученные значения z, p, v подставляют в уравнение Бернулли:
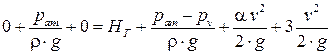 .
.
Упрощая полученное уравнение, найдем показание вакуумметра:
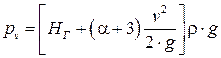 .
.
Найдём расход жидкости в трубе:
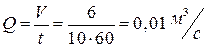 .
.
Находим скорость в трубе:
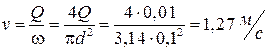 .
.
Находим давление:
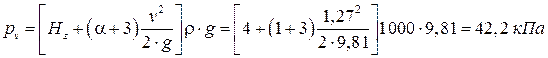 .
.
Ответ: pv = 42,2 кПа.
Задача 2.1
 По тройнику движется жидкость. Определить скорости движения жидкости в сечениях, если Q1 = 0,0314 м3/с, Q2 = 0,0157 м3/с, а диаметры сечений равны d2 = 0,2 м, d1 = d3 = 0,1 м По тройнику движется жидкость. Определить скорости движения жидкости в сечениях, если Q1 = 0,0314 м3/с, Q2 = 0,0157 м3/с, а диаметры сечений равны d2 = 0,2 м, d1 = d3 = 0,1 м |
Задача 2.2
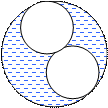 Определить эквивалентный диаметр для потока и скорость движения жидкости в поперечном сечении (затемненная область), если за 100 секунд прокачивается 3,14 м3 воды, а диаметры равны D = 0,2 м, d = 0,1 м. Определить эквивалентный диаметр для потока и скорость движения жидкости в поперечном сечении (затемненная область), если за 100 секунд прокачивается 3,14 м3 воды, а диаметры равны D = 0,2 м, d = 0,1 м. |
Задача 2.3
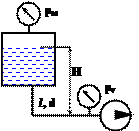 Вода из бака перекачивается насосом с расходом 2 л/с по трубопроводу диаметром 30 мм. Высота уровня воды в баке H = 10 м. Давление вакуума на входе в насос pv = 0,03 МПа. Потери напора h1-2 = 7 V2/2g. Рассчитать давление в баке pм. Вода из бака перекачивается насосом с расходом 2 л/с по трубопроводу диаметром 30 мм. Высота уровня воды в баке H = 10 м. Давление вакуума на входе в насос pv = 0,03 МПа. Потери напора h1-2 = 7 V2/2g. Рассчитать давление в баке pм. |
Задача 2.4
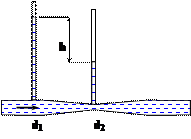 В водомере Вентури разность уровней пьезометров равна h = 0,5 м. Определить расход, если диаметры равны d1 = 0,3 м. d2 = 0,2 м. Потери напора считать равными h1-2 =0,06 V22/2g. В водомере Вентури разность уровней пьезометров равна h = 0,5 м. Определить расход, если диаметры равны d1 = 0,3 м. d2 = 0,2 м. Потери напора считать равными h1-2 =0,06 V22/2g. |