МОМЕНТ импульса. Законы сохранения МОМЕНТА импульса. Работа и энергия при Вращательнм движении

Список основных формул

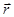момент импульса м.т. ( ) – векторная физическая величина, определяемая векторным произведением вектора , соединяющего м.т. с осью вращения и перпендикулярного к этой оси, и вектора импульса тела :

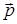, (4.1)

где 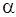– угол между векторам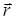и и 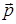, 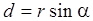– прицельное расстояние (кратчайшее расстояние между осью вращения и линией движения тела).

момент импульса а.т.т. ( 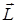) относительно оси вращения – векторная физическая величина, равная векторной сумме моментов импульсов всех точек этого тела.

Основной закон динамики вращательного движения

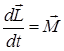(4.2)

Закон сохранения момента импульса

Суммарный момент импульса замкнутой системы тел остается постоянным относительно любой оси вращения:

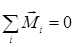Þ или 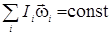. (4.3)

В данном случае под замкнутой системой тел подразумевается система тел, на которые не действуют моменты внешние силы ( 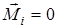) или их сумма равна нулю ( ).

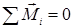Работа сил при вращательном движении (теорема о кинетической энергии для вращающегося тела)

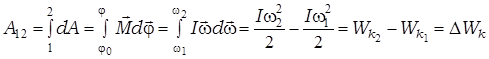(4.4)

Кинетическая энергия тела при вращении тела вокруг одной оси

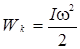(4.5)

в случае катящегося тела

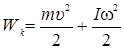(4.6)

Список основных формул.

Количество вещества (число молей газа)

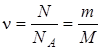, (5.1)

где N – число молекул; N_A = 6,02^.10²³ моль^-1– постоянная Авогадро, m – масса газа, M – молярная масса газа.

Плотность газа

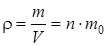, (5.2)

где n – концентрация газа (число молекул в единице объема), m₀ – масса молекулы газа.

Уравнение Клапейрона–Менделеева (уравнение состояния идеального газа)

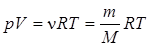,(5.3)

где V – объем газа; p – давление газа; Т – абсолютная температура; R = 8,31 Дж/(моль×К) – универсальная газовая постоянная.

Закон Бойля – Мариотта (изотермический процесс, Т = const)

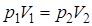. (5.4)

Закон Гей-Люссака (изобарический процесс, p = const)

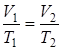. (5.5)

Закон Шарля (изохорический процесс, V = const.)

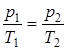. (5.6)

Закон Дальтона для давления смеси газов

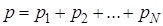(5.7)

где p₁, p₂, … , p_N – парциальные давления газов, находящихся в смеси (парциальное давление – такое давление, которое газ при данной температуре оказывал бы на стенки сосуда, если бы он один заполнял весь объем).

Основное уравнение молекулярно – кинетической теории (МКТ)

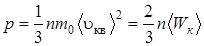, (5.8)

где 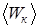– средняя кинетическая энергия теплового движения молекулы газа; k= 1,38×10-23Дж/К – постоянная Больцмана; 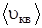– среднеквадратическая скорость молекул.

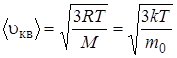. (5.9)

Связь между давлением идеального газа и температурой

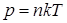. (5.10)

Средняя кинетическая энергия одной молекулы

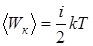, (5.11)

где i – число степеней свободы молекулы (i = 3 – для одноатомного газа; i= 5 – для двухатомного газа, i = 6 – для многоатомного газа)

Функция распределения молекул по модулю скорости (функции распределения Максвелла)

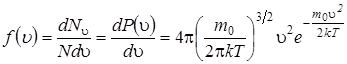(5.12)

Наиболее вероятная скорость молекул идеального газа вычисляется по формуле:

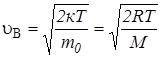, (5.13)

Средняя скорость теплового движения молекул

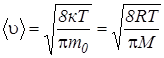. (5.14)

Барометрическая формула – описывает распределение давления по высоте в атмосфере Земли и других планет:

, (5.15)

где р – давление газа на высоте h; р₀ – давление газа на высоте h = 0; g – ускорение свободного падения.

Зависимость концентрации молекул газа от высоты

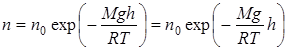(5.16)

где n – концентрация молекул на высоте h; n₀ – концентрация молекул на высоте h = 0

Молярные теплоемкости при постоянном объеме c_v и постоянном давлении c_p соответственно равны

. (5.17)

Связь между молярной (c) и удельной (с_уд) теплоемкостями газа

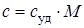. (5.18)

где М – молярная масса газа.

Внутренняя энергия идеального газа – суммарная кинетическая энергия молекул газа

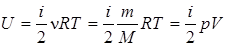. (5.19)

Работа равновесного расширения газа при изменении объема от V₁ до V₂

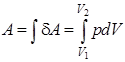. (5.20)

Первое начало термодинамики: количество теплоты, подведенное к системе, идет на изменение ее внутренней энергии и на работу, совершаемую системой над внешними телами

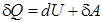, (5.21)

где δQ и δA означают элементарное количество теплоты и элементарную работу в ходе процесса, при котором внутренняя энергия системы изменилась на бесконечно малую величину dU.

Первое начало термодинамики для процесса, при котором изменение параметров системы является конечным можно записать в виде

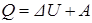, (5.22)

где Q –конечное количество тепла, сообщенное термодинамической системе (газу) или отданное ею; DU – конечное изменение внутренней энергии системы; А –полная работа, совершенные термодинамической системой.

Применение первого начала термодинамики к различным процессам::

1. Изотермический процесс: Т = const, DU = 0,

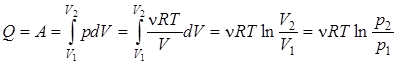. (5.23)

2. Изохорический процесс: V = const, 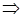A = 0,

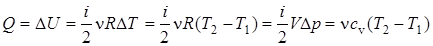. (5.24)

3. Изобарический процесс: p = const.

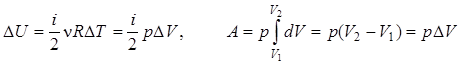
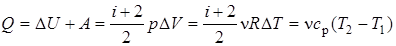. (5.25)

4. Адиабатический процесс: Q = 0,

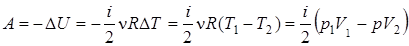. (5.26)

Уравнение Пуассона (уравнение газового адиабатного процесса)

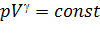, (5.27)

где 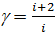– показатель адиабаты (коэффициент Пуассона)

5. Круговой процесс (цикл): DU_кр = U₁ – U₁ = 0,

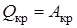. (5.28)