Применение теории Бора к атому водорода

Для объяснения спектра атомарного водорода Бор, основываясь на своих постулатах, сделал предположение, что в атоме водорода стационарными, разрешенными, устойчивыми орбитами являются только те орбиты, для которых момент импульса электрона равен целому кратному постоянной Планка, деленной на 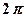, т.е.

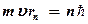(19)

где 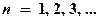- главное квантовое число, 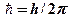, 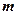- масса электрона, 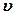- скорость электрона, 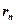- радиус орбиты электрона.

Исходя из этих представлений, вычислим радиусы стационарных орбит.

Рассмотрим электрон, движущийся в поле атомного ядра с зарядом 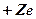. При 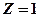такая система соответствует атому водорода, при иных 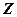- водородоподобному иону, т.е. атому с порядковым номером 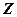, из которого удалены все электроны, кроме одного.

На электрон действует кулоновская сила притяжения к ядру, которая является центростремительной. Согласно второму закону Ньютона

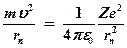(20)

Из (19) получаем: 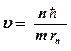. Подставляем в (20):

.

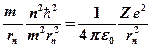Получаем радиус 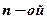орбиты электрона:

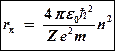. (21)

Для первой орбиты атома водорода ( 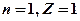) получим:

,

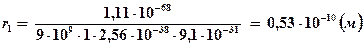т.е. порядка газокинетических размеров атома.

Энергия электрона в атоме слагается из его потенциальной энергии в электрическом поле ядра:

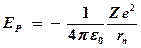
и кинетической энергии его движения по орбите со скоростью :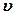

.

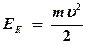Таким образом, полная энергия электрона 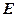равна:

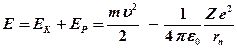. (22)

Из формулы (20) получаем

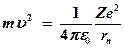. (23)

Подставляя (23) в (22) получаем выражение для полной энергии:

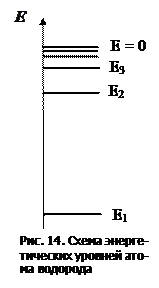
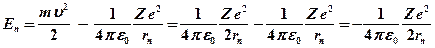
Подставляя в это выражение значение радиуса из (21), получим:

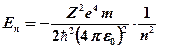
Таким образом, схема энергетических уровней атома водорода будет иметь вид, изображенный на рис. 14.

Согласно формуле (18) при переходе электрона из одного энергического состояния в другое испускается квант электромагнитной волны с энергией:

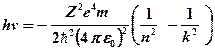
Следовательно, частота излучаемого света будет равна:

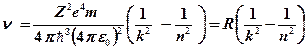. (24)

Сравнивая (24) и (16), получим, что постоянная Ридберга должна определяться выражением:

.

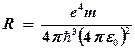Таким образом, получено теоретическое выражение для постоянной Ридберга. Подставляя значения универсальных констант, получаем:

.

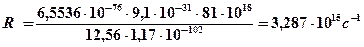Полученное значение очень хорошо согласуется с экспериментальным значением, найденным из спектроскопических данных.

Подставляя в формулу (15) 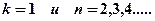, получим группу линий, образующих серию Лаймана (24) и соответствующих переходам электронов с возбуждённых уровней ( 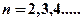) на основной ( 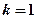). Аналогично, при подстановке 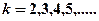и соответствующих им значений 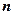, получим серии Бальмера, Пашена, Пфунда и т.д.

Следовательно по теории Бора спектральные серии соответствуют излучению, возникающему в результате перехода атомов в данное состояние из возбуждённых состояний, расположенных выше данного.

Итак, теория атома Бора в применении к атому водорода дала поразительно точные результаты.

Теория Бора показала, что к внутриатомным процессам нельзя применять понятия классической физики.

Опыты Франка и Герца

Согласно постулатам Бора уровни энергий внутри атома должны принимать дискретные значения.

Изучая методом задерживающего потенциала столкновения электронов с атомами газов в 1913 году Д.Франк и Г.Герц экспериментально доказали дискретность значений энергии атомов.

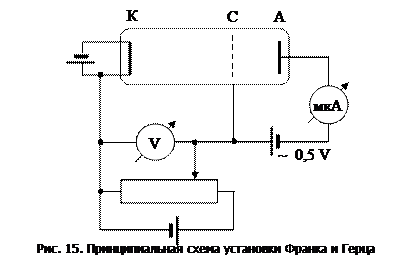
Принципиальная схема установки Франка и Герца приведена на рис. 15. В трубке находятся пары ртути при низком давлении (порядка

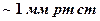). За счет термоэлектронной эмиссии из катода 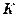вылетают электроны, которые ускоряются разностью потенциалов, приложенной между катодом и сеткой. Между сеткой и анодом 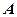создавалось слабое электрическое поле, тормозившее движение электронов к аноду. Определялась зависимость
анодного тока от напряжения между катодом и сеткой. Такая зависимость приведена на рис. 16.

До тех пор пока энергия электронов меньше энергии первого уровня возбуждения атомов ртути, соударения электронов с атомами ртути носят упругий характер. При таких соударениях электроны почти не теряют свою энергию, проскакивают через сетку 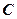и все электроны участвуют в создании анодного тока. Когда же энергия электронов достигает или превосходит энергию первого уровня возбуждения атомов ртути, происходит неупругое соударение. Электроны передают энергию атомам, они возбуждаются, а сами электроны теряют свою энергию. Поэтому резко уменьшается число электронов, проскочивших через сетку 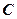и достигших анода 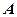. Анодный ток резко падает. При дальнейшем увеличении анодного напряжения, энергия электронов также растет и превышает первый уровень энергии возбуждения атомов ртути. Соударения опять становятся упругими, все электроны проскакивают сетку, и анодный ток вновь растет. Растет и энергия электронов. Однако, при достижении электронами энергии второго уровня возбуждения атомов ртути, соударения становятся неупругими, и опять происходит падение анодного тока. То же происходит и для третьего уровня возбуждения.

Таким образом, эксперимент Франка и Герца показывает, что уровни энергий атомов ртути имеют дискретный характер, что подтверждает постулаты Бора.