Кинематика вращательного движения.
Угловая скорость.
ОПРЕДЕЛЕНИЕ: Вращательным движением будем называть такое движение, при котором все точки абсолютно твердого тела описывают окружности, центры которых лежат на одной прямой, называемой осью вращения.
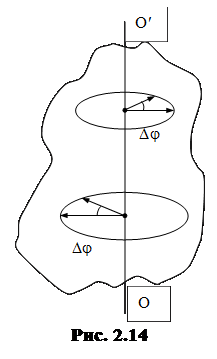 В качестве координаты, определяющей положение точки при вращательном движении, берут угол, характеризующий мгновенное положение радиус-вектора, проведенного из центра вращения к рассматриваемой точке (рис. 2.14)
В качестве координаты, определяющей положение точки при вращательном движении, берут угол, характеризующий мгновенное положение радиус-вектора, проведенного из центра вращения к рассматриваемой точке (рис. 2.14)
Для характеристики вращательного движения вводится понятие угловой скорости
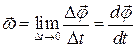 .
.
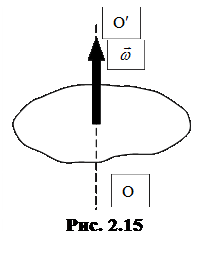
Вектор 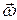 направлен вдоль оси, вокруг которой вращается тело в сторону, определяемую правилом правого винта (рис. 2.15).
направлен вдоль оси, вокруг которой вращается тело в сторону, определяемую правилом правого винта (рис. 2.15).
Модуль вектора угловой скорости равен 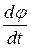 . Если
. Если 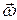 = const, то такое движение называется равномерным, при этом
= const, то такое движение называется равномерным, при этом 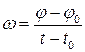 , следовательно
, следовательно 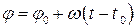 и при t0 = 0 получаем
и при t0 = 0 получаем 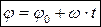 .
.
Если j0 = 0, то j = w·t или 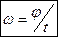 .
.
Таким образом, при равномерном движении w показывает на какой угол поворачивается тело за единицу времени. Размерность угловой скорости [w]=рад/сек.
Равномерное вращение можно характеризовать периодом вращения T, под которым понимают время, за которое тело делает один полный оборот, т.е. поворачивается на угол 2p. В этом случае 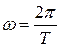 , следовательно
, следовательно 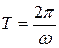 .
.
 Частота вращения (число оборотов в единицу времени): n=1/T=w/2p. Отсюда w=2pn.
Частота вращения (число оборотов в единицу времени): n=1/T=w/2p. Отсюда w=2pn.
Дополнение 1.
Поворот тела на некоторый малый угол dj можно задать в виде отрезка, длина которого равна dj, а направление совпадает с осью, вокруг которой совершен поворот. Таким образом, повороту тела можно приписать некоторое численное значение и направление. При этом направление вектора 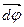 можно определить, связав его с направлением вращения тела. Такие вектора называются аксиальными или псевдовекторами, в отличие от истинных или полярных векторов, для которых направление определяется естественным образом (
можно определить, связав его с направлением вращения тела. Такие вектора называются аксиальными или псевдовекторами, в отличие от истинных или полярных векторов, для которых направление определяется естественным образом ( 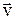 ,
, 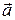 ,
, 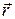 и т. д.), при операции инверсии системы координат(x → -x’, y → -y’, z → -z’) последние меняют знак на противоположный:
и т. д.), при операции инверсии системы координат(x → -x’, y → -y’, z → -z’) последние меняют знак на противоположный: 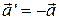 .
.
Угловое ускорение.
Вектор угловой скорости 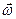 может изменяться как за счет изменения скорости вращения тела вокруг оси (в этом случае он изменяется о величине), так и за счет поворота оси вращения в пространстве (в этом случае
может изменяться как за счет изменения скорости вращения тела вокруг оси (в этом случае он изменяется о величине), так и за счет поворота оси вращения в пространстве (в этом случае 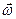 изменяется по направлению). Для характеристики быстроты изменения
изменяется по направлению). Для характеристики быстроты изменения 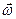 вводится физическая величина
вводится физическая величина 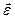 , называемая угловым ускорением.
, называемая угловым ускорением.
ОПРЕДЕЛЕНИЕ: Средним угловым ускорением называется величина 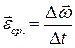 , где Dt – промежуток времени за который произошло изменение угловой скорости.
, где Dt – промежуток времени за который произошло изменение угловой скорости.
ОПРЕДЕЛЕНИЕ: Мгновенным ускорением 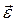 называется величина равная
называется величина равная 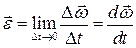 ;
;
Если направление оси вращения в пространстве постоянно, то угловая скорость изменяется только по величине 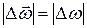 и в этом случае
и в этом случае 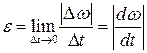 .
.
Если под e понимать проекцию вектора 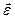 на направление
на направление 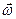 , то последняя формула примет вид
, то последняя формула примет вид 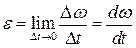 . Здесь e – алгебраическая величина и
. Здесь e – алгебраическая величина и
если w , то e>0 (векторы 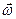 и
и 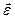 одного направления),
одного направления),
 если w ¯, то e<0 (
если w ¯, то e<0 ( 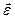 ¯
¯ 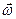 ).
).
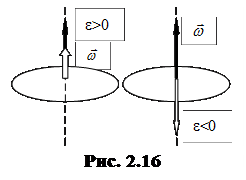
1) Если e>0 Þ вращение равноускоренное ( 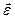
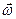 ) (рис. 2.16).
) (рис. 2.16).
2) Если e<0 – ( 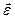 ¯
¯ 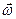 ) (рис. 2.16).
) (рис. 2.16).
В системе СИ [e]=рад/с2.
Для равноускоренного движения:
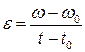
Следовательно, w = w0 + e·(t - t0). При t0 = 0 получаем w = w0 + e·t.
Тогда 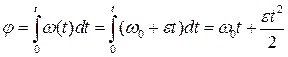 ;
;
Окончательно
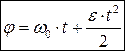 (2.6)
(2.6)
Теперь установим
