Закон ома в дифференциальной форме

Немецкий физик Г. Ом (1787 – 1854) экспериментально установил, что сила тока на участке, не содержащем ЭДС прямо пропорциональна напряжению:

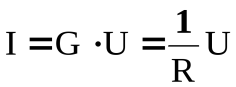, (11)

где коэффициент пропорциональности G = 1 / R и называется электрической проводимостью проводника. Для линейных проводников с постоянным поперечным сечением

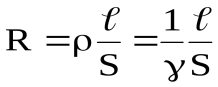, (12)

где γ = 1 / ρ – удельная электропроводность материала, ρ – удельное сопротивление,S – площадь поперечного сечения проводника, 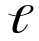– его длина. Тогда для изотропного проводника выражение (11) с учётом (12) примет вид:

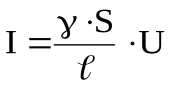. (13)

Теперь для плотности тока (2) с учётом, что 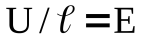– напряжённость поля в проводнике, получим:

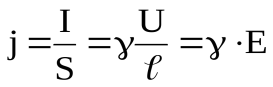. (14)

Выражение (14) в векторной форме это закон Ома в дифференциальной форме:

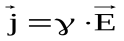. (15)

Получим в дифференциальной форме закон Джоуля-Ленца. Количество теплоты, выделяющееся в элементе проводника, объёмом 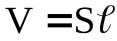за времяdt:

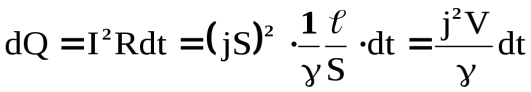. (16)

Теперь, количество теплоты, которое выделяется в единице объема проводника за единицу времени, будет:

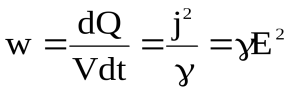. (17)

Эта величина называется удельной тепловой мощностью тока.

II. Электрическое сопротивление проводника

Электрическое сопротивление проводника: 1) величина, характеризующая противодействие проводника или электрической цепи электрическому току;

2) структурный элемент электрической цепи, включаемый в цепь для ограничения или регулирования силы тока.

Электрическое сопротивление металлов зависит от материала проводника, его длины и поперечного сечения, температуры и состояния проводника (давления, механических сил растяжения и сжатия, т.е. внешних факторов, влияющих на кристаллическое строение металлических проводников).

Зависимость сопротивления от материала, длины и площади поперечного сечения проводника:

,

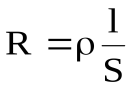где r - удельное сопротивление проводника;

l – длина проводника;

S – площадь поперечного сечения проводника.

Обобщенный закон Ома в интегральной форме для участка цепи и полной цепи.

Обобщенный закон Ома в интегральной форме для участка цепи: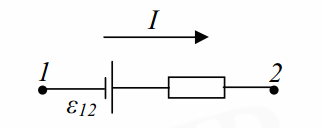

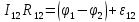
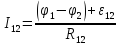
где 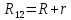– электрическое сопротивление участка цепи 1-2, 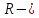сопротивление внешней цепи, 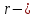внутреннее сопротивление источника ЭДС;

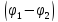–разность потенциалов на участке цепи 1-2.

Закон Ома для неоднородного участка цепи: Произведение электрического сопротивления участка цепи на силу тока в нем равно сумме падения электрического потенциала на этом участке и ЭДС всех источников электрической энергии, включенных на данном участке.

Правило знаков для ЭДС: если напряженность поля сторонних сил в источнике совпадает с направлением выбранного обхода, то при подсчете ЭДС этого источника нужно считать положительным, в противном случае - отрицательным.

Закон Ома для полной цепи:Если электрическая цепь замкнута, то 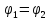, тогда

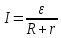
где ε – алгебраическая сумма отдельных ЭДС в данной цепи, 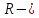сопротивление внешней цепи, 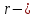внутреннее сопротивление источника тока.

Напряжение на участке цепи.

Под напряжением на некотором участке электрической цепи понимают разность потенциалов между крайними точками этого участка.

На рис. 13 изображен участок цепи, на котором есть резистор сопротивлением 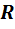и нет ЭДС. Крайние точки этого участка обозначены буквами a и b. Пусть ток течет от точки a к точке b.

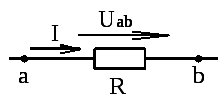
Рис. 13. Участок электрической цепи

На участке без ЭДС ток течет от более высокого потенциала к более низкому. Следовательно, потенциал 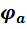точки a выше потенциала 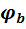точки bна величину, равную произведению тока 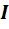на сопротивление :

.

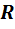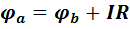В соответствии с определением, напряжение между точками a и b

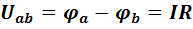.(8)

Другими словами, напряжение на резисторе равно произведению тока, протекающего по резистору, на величину сопротивления этого резистора.

В электротехнике разность потенциалов на концах резистора принято называть либо «напряжением на резисторе», либо «падением напряжения». В литературе встречаются оба этих определения.

Рассмотрим теперь вопрос о напряжении на участке цепи, содержащем не только резистор, но и источник ЭДС.

На рис. 14 а и б показаны участки некоторых цепей, по которым протекает ток 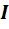.. Найдем напряжение между точками a и c для этих участков.

а) б)

Рис. 14. Участки электрической цепи

По определению

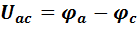.(9)

Выразим потенциал точки a через потенциал точки c. При перемещении от точки c к точке b (рис. 14,а) идем встречно ЭДС 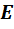, поэтому потенциал точки b оказывается меньше, чем потенциал точки c на величину ЭДС 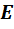, т.е.

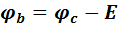.(10)

На рис. 14,б при перемещении от точки c к точке b идем согласно ЭДС 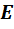и потому потенциал точки b оказывается больше, чем потенциал точки cна величину ЭДС 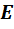, т.е.

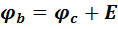.(11)

Ранее говорилось, что на участке цепи без ЭДС ток течет от более высокого потенциала к более низкому. Поэтому в обеих схемах рис. 14 потенциал точки a выше, чем потенциал точки b на величину падения напряжения на резисторе сопротивлением :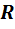

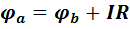. (12)

Таким образом, для рис. 14,а имеем

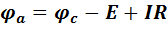, или

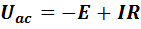.(13)

И для рис. 14, б имеем

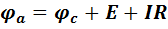, или

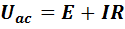.(14)

Положительное направление напряжения указывают на схемах стрелкой. Стрелка должна быть направлена от первой буквы индекса ко второй. Так, положительное направление напряжения 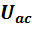изобразится стрелкой, направленной от a к c.

Из самого определения напряжения следует также, что 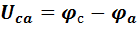. Поэтому 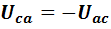. Другими словами, изменение чередования индексов равносильно изменению знака этого напряжения. Из изложенного ясно, что напряжение может быть и положительной, и отрицательной величиной.